Adam和学习率衰减(learning rate decay)
本文先介绍一般的梯度下降法是如何更新参数的,然后介绍 Adam 如何更新参数,以及 Adam 如何和学习率衰减结合。
梯度下降法更新参数
梯度下降法参数更新公式:
其中,\(\eta\) 是学习率,\(\theta_t\) 是第 \(t\) 轮的参数,\(J(\theta_t)\) 是损失函数,\(\nabla J(\theta_t)\) 是梯度。
在最简单的梯度下降法中,学习率 \(\eta\) 是常数,是一个需要事先设定好的超参数,在每轮参数更新中都不变,在一轮更新中各个参数的学习率也都一样。
为了表示简便,令 \(g_t = \nabla J(\theta_t)\),所以梯度下降法可以表示为:
Adam 更新参数
Adam,全称 Adaptive Moment Estimation,是一种优化器,是梯度下降法的变种,用来更新神经网络的权重。
Adam 更新公式:
在 Adam 原论文以及一些深度学习框架中,默认值为 \(\eta = 0.001\),\(\beta_1 = 0.9\),\(\beta_2 = 0.999\),\(\epsilon = 1e-8\)。其中,\(\beta_1\) 和 \(\beta_2\) 都是接近 1 的数,\(\epsilon\) 是为了防止除以 0。\(g_{t}\) 表示梯度。
咋一看很复杂,接下一一分解:
- 前两行:
这是对梯度和梯度的平方进行滑动平均,使得每次的更新都和历史值相关。
- 中间两行:
这是对初期滑动平均偏差较大的一个修正,叫做 bias correction,当 \(t\) 越来越大时,\(1-\beta_{1}^{t}\) 和 \(1-\beta_{2}^{t}\) 都趋近于 1,这时 bias correction 的任务也就完成了。
- 最后一行:
这是参数更新公式。
学习率为 \(\frac{\eta}{\sqrt{\hat{v}_{t}}+\epsilon}\),每轮的学习率不再保持不变,在一轮中,每个参数的学习率也不一样了,这是因为 \(\eta\) 除以了每个参数 \(\frac{1}{1- \beta_2} = 1000\) 轮梯度均方和的平方根,即 \(\sqrt{\frac{1}{1000}\sum_{k = t-999}^{t}g_k^2}\)。而每个参数的梯度都是不同的,所以每个参数的学习率即使在同一轮也就不一样了。(可能会有疑问,\(t\) 前面没有 999 轮更新怎么办,那就有多少轮就算多少轮,这个时候还有 bias correction 在。)
而参数更新的方向也不只是当前轮的梯度 \(g_t\) 了,而是当前轮和过去共 \(\frac{1}{1- \beta_1} = 10\) 轮梯度的平均。
有关滑动平均的理解,可以参考我之前的博客:理解滑动平均(exponential moving average)。
Adam + 学习率衰减
在 StackOverflow 上有一个问题 Should we do learning rate decay for adam optimizer - Stack Overflow,我也想过这个问题,对 Adam 这些自适应学习率的方法,还应不应该进行 learning rate decay?
论文 《DECOUPLED WEIGHT DECAY REGULARIZATION》的 Section 4.1 有提到:
Since Adam already adapts its parameterwise learning rates it is not as common to use a learning rate multiplier schedule with it as it is with SGD, but as our results show such schedules can substantially improve Adam’s performance, and we advocate not to overlook their use for adaptive gradient algorithms.
上述论文是建议我们在用 Adam 的同时,也可以用 learning rate decay。
我也简单的做了个实验,在 cifar-10 数据集上训练 LeNet-5 模型,一个采用学习率衰减 tf.keras.callbacks.ReduceLROnPlateau(patience=5),另一个不用。optimizer 为 Adam 并使用默认的参数,\(\eta = 0.001\)。结果如下:
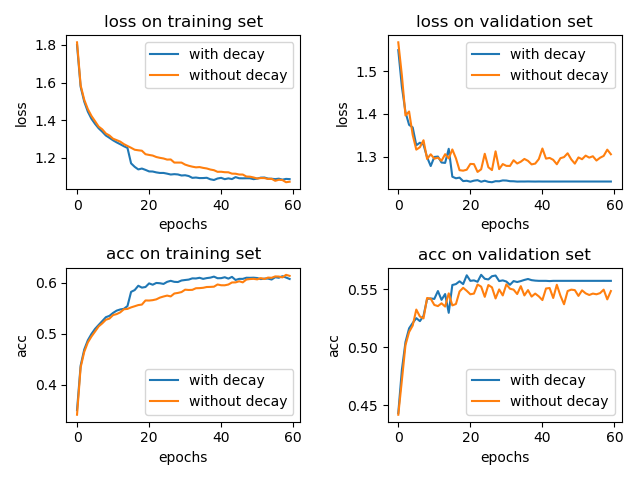
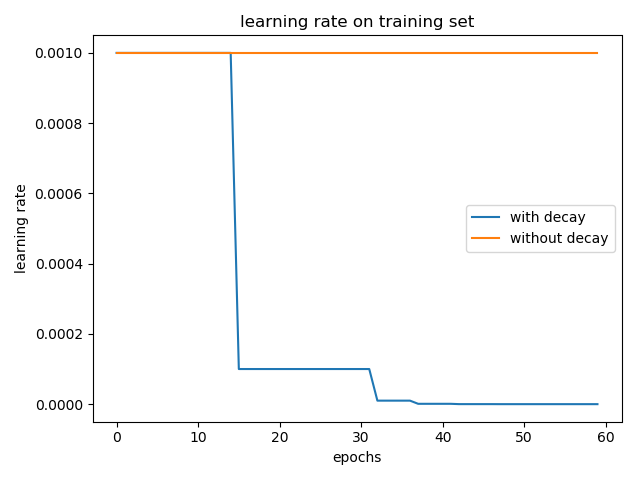
加入学习率衰减和不加两种情况在 test 集合上的 accuracy 分别为: 0.5617 和 0.5476。(实验结果取了两次的平均,实验结果的偶然性还是有的)
通过上面的小实验,我们可以知道,学习率衰减还是有用的。(当然,这里的小实验仅能代表一小部分情况,想要说明学习率衰减百分之百有效果,得有理论上的证明。)
当然,在设置超参数时就可以调低 \(\eta\) 的值,使得不用学习率衰减也可以达到很好的效果,只不过参数更新变慢了。
将学习率从默认的 0.001 改成 0.0001,epoch 增大到 120,实验结果如下所示:
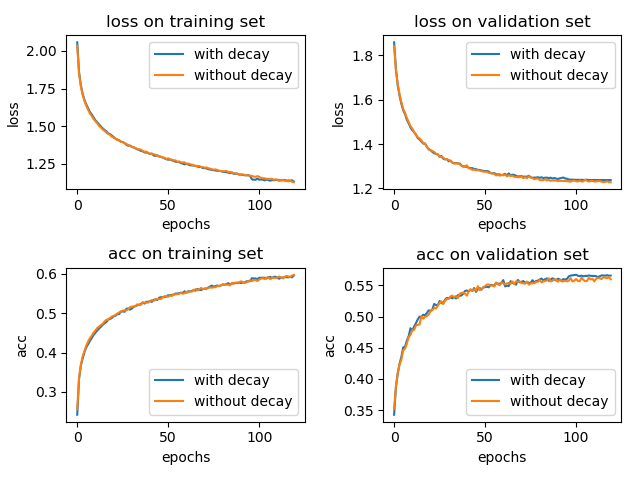
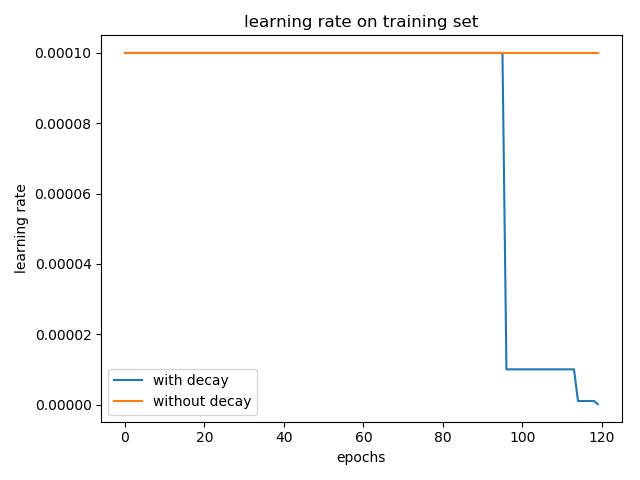
加入学习率衰减和不加两种情况在 test 集合上的 accuracy 分别为: 0.5636 和 0.5688。(三次实验平均,实验结果仍具有偶然性)
这个时候,使用学习率衰减带来的影响可能很小。
那么问题来了,Adam 做不做学习率衰减呢?
我个人会选择做学习率衰减。(仅供参考吧。)在初始学习率设置较大的时候,做学习率衰减比不做要好;而当初始学习率设置就比较小的时候,做学习率衰减似乎有点多余,但从 validation set 上的效果看,做了学习率衰减还是可以有丁点提升的。
ReduceLROnPlateau 在 val_loss 正常下降的时候,对学习率是没有影响的,只有在 patience(默认为 10)个 epoch 内,val_loss 都不下降 1e-4 或者直接上升了,这个时候降低学习率确实是可以很明显提升模型训练效果的,在 val_acc 曲线上看到一个快速上升的过程。对于其它类型的学习率衰减,这里没有过多地介绍。
Adam 衰减的学习率
从上述学习率曲线来看,Adam 做学习率衰减,是对 \(\eta\) 进行,而不是对 \(\frac{\eta}{\sqrt{\hat{v}_{t}}+\epsilon}\) 进行,但有区别吗?
学习率衰减一般如下:
-
exponential_decay:
decayed_learning_rate = learning_rate * decay_rate ^ (global_step / decay_steps) -
natural_exp_decay:
decayed_learning_rate = learning_rate * exp(-decay_rate * global_step / decay_steps) -
ReduceLROnPlateau
如果被监控的值(如‘val_loss’)在 patience 个 epoch 内都没有下降,那么学习率衰减,乘以一个 factor
decayed_learning_rate = learning_rate * factor
这些学习率衰减都是直接在原学习率上乘以一个 factor ,对 \(\eta\) 或对 \(\frac{\eta}{\sqrt{\hat{v}_{t}}+\epsilon}\) 操作,结果都是一样的。
References
[1] An overview of gradient descent optimization algorithms -- Sebastian Ruder
[2] Should we do learning rate decay for adam optimizer - Stack Overflow
[3] Tensorflow中learning rate decay的奇技淫巧 -- Elevanth
[4] Loshchilov, I., & Hutter, F. (2017). Decoupled Weight Decay Regularization. ICLR 2019. Retrieved from http://arxiv.org/abs/1711.05101


 浙公网安备 33010602011771号
浙公网安备 33010602011771号