Codeforces Round #641 (Div. 2) E. Orac and Game of Life

　　写下这篇题解时，已经接近深夜一点。

　　小县城已经进入睡眠，但中心广场这里，深夜的寂静仍然时常被十字交通路口的车声与广场上悉悉索索的谈话声所打断。房间里吸顶灯兢兢业业地工作着，一窗将灯火通明的房间与外面的黑暗分隔开来。我默默地坐在电脑前补刚刚比赛时没能做出来的E题，已经提交两次了但都WA在了test5上，无奈之下重写了一遍代码，十分钟后提交上去却错误如故。我内心一阵阵烦躁，代码在编辑器里被翻来覆去，又仔细地检查了十分钟，确定是逻辑上确实是没问题，那么就可能是看题看走眼了。返回题面再看看，哦，p有点大，int会溢出，改long long后，过了。

　　ACMer的日常。

---

 

题面：给个n*m的网格，里面一些格子一开始是白色(0)，另一些是黑色(1)，接下来网格可进行迭代，对于每次迭代，格子里颜色的变化遵循以下规则：

1.若该格子有相邻格子的颜色与之相同，则颜色翻转

2.若该格子没有相邻格子的颜色与之相同，则颜色不变

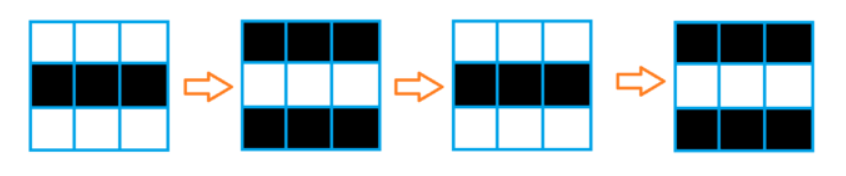
有t次询问，每次询问都有i, j, p，表示问第i行第j列格子在第p次迭代后是什么颜色。

 原题链接：https://codeforces.ml/contest/1350/problem/E

---

分析：由上图观察我们就能发现，当某一格子可以变色的话，那么在那之后每次迭代颜色都会翻转，也就是说，我们只要算出来每个格子在第几次迭代会开始变色即可，而这个能简化成一个最短路模型来进行宽搜。

详细步骤：

Step1:设dist[i][j]表示第(i, j)个格子在dist[i][j]次迭代后会开始变色

Step2:初始dist数组的值为inf

Step3:对一开始就能变色的格子进行深搜，设其dist[x][y] = 0，并把该格子加入宽搜队列

Step4:进行宽搜，把宽搜队列中的元素取出来进行四联通的搜索，如果有dist[x][y] + 1 < dist[xx][yy]，那么dist[xx][yy]更新并将第(xx, yy)格子加入宽搜队列

Step5:对于dist[x][y]为inf的格子，说明不管怎么迭代永远都不会变色，p < dist[x][y]时，说明直到该次迭代都没有变色，p >= dist[x][y]时，若p - dist[x][y]是奇数就说明这次迭代与初始色相反，偶数就是与初始色相同

---

AC代码（注：在代码中询问的p变成了z）

#include <bits/stdc++.h>
#define rep(i, l, r) for(long long i=l; i<=r ;i++)
using namespace std;

typedef long long ll;
typedef pair<int, int> PII;
typedef vector<int> VI;
ll gcd(ll n, ll m) { return n % m == 0 ? m : gcd(m, n % m);}

const int Maxn = 1e3 + 10;
const int inf  = 0x3f3f3f3f;

char Map[Maxn][Maxn];
ll dist[Maxn][Maxn];
bool visit[Maxn][Maxn];
int dx[4] = {0, 1, 0, -1};
int dy[4] = {1, 0, -1, 0};
queue<PII> q;

void Ini()
{
    memset(dist, inf, sizeof(dist));
    rep(i, 0, Maxn-1)
        rep(j, 0, Maxn-1)
            Map[i][j] = -1;
}

void dfs(int x, int y)
{
    visit[x][y] = true;
    dist[x][y] = 0;
    q.push(PII(x, y));
    rep(i, 0, 3){
        int xx = dx[i];
        int yy = dy[i];

        if(Map[xx][yy] == Map[x][y] && !visit[xx][yy])
            dfs(xx, yy);
    }
}

void bfs()
{
    while(!q.empty()){
        PII p = q.front(); q.pop();
        rep(i, 0, 3){
            int xx = p.first + dx[i];
            int yy = p.second + dy[i];

            if(Map[xx][yy] != -1 && dist[p.first][p.second] + 1 < dist[xx][yy]){
                dist[xx][yy] = dist[p.first][p.second] + 1;
                q.push(PII(xx, yy));
            }
        }
    }
}

int main()
{
    ios::sync_with_stdio(false);
    //freopen("data.txt", "r", stdin);
    //freopen("output.txt", "w", stdout);
    Ini();
    int n, m, t;
    cin>>n>>m>>t;
    rep(i, 1, n){
        cin>>(Map[i] + 1);
        Map[i][m+1] = -1;
    }
        
    
    rep(i, 1, n)
        rep(j, 1, m)
            Map[i][j] -= '0';
    
    rep(i, 1, n)
        rep(j, 1, m){
            rep(k, 0, 3){
                int xx = i + dx[k];
                int yy = j + dy[k];
                if(Map[xx][yy] == Map[i][j]){
                    dfs(i, j);
                    break;
                }
            }
        }

    bfs();

    while(t--){
        ll x, y, z;
        cin>>x>>y>>z;
        if(dist[x][y] == inf) cout<<int(Map[x][y])<<endl;
        else{
            if(z <= dist[x][y]) cout<<int(Map[x][y])<<endl;
            else if((z - dist[x][y]) & 1) cout<<1 - Map[x][y]<<endl;
            else cout<<int(Map[x][y])<<endl;
        }
    }

    return 0;
}