从零开始的树状数组
树状数组好久没写了,最近又要写起来时发现自己竟然已经忘记,又得从网上找博客复习,但是这看着看着,就突然发现这些博客所讲的树状数组大多都是太过于理论化,推导的思维也很飞跃式,把树状数组当成了一种数学上的trick,这就导致了学习树状数组也不过是把这种数学trick背下来而已,估计这就是导致我在日久不用的过程中把树状数组忘记的原因吧。
但是仔细想想,树状数组真的只是偶然发现的单纯地运用lowbit的数学游戏而没有原型的东西而已吗?3Blue1Brown的数学视频告诉我一般一个数学理论,都是有它的起源,并从那一步步推导过来的。
现在就想用这篇博客,从不知道树状数组这个概念开始,从零去探索这个树状数组。
OK,现在你并不知道树状数组是什么东西。树状数组?那是什么?能吃吗?你现在只是一个单纯的问题研究者。
你最近对前缀和的问题很感兴趣
有一个下标从1到n数组,然后有很多个前缀和查询,怎么去高效地应对这些查询呢?

说到前缀和,很自然的想法就是去直接维护前缀和。这样每次查询O(1)就可以搞定了。

问题变化了一下,这个数组有很多次单点修改操作,然后有很多个在线的前缀和查询,你仍然要高效地让程序正确输出每次查询。
直接维护前缀和就不行了,因为每次对数组某个位置的修改,就得把前缀和的数组从那个位置到尾部全部修改一遍,这样操作的时间复杂度是O(n),修改一多就不是很高效。
然后你就得思考一种单点修改和查询都很快的算法。
直接维护前缀和的话单个元素的影响力太大了,每个元素都牵连了后面所有元素,这就使得修改起来很不方便。那有没有方法让每个元素牵连的其他元素都少点呢?
然后你想到了把一个数组用二分去划分成多个区间和,即[1, n]、[1, n/2]、[n/2+1, n]、[1, n/2/2]......然后前缀和就是这某些不重叠区间的相加,下面是用上图所表示的数组作为例子



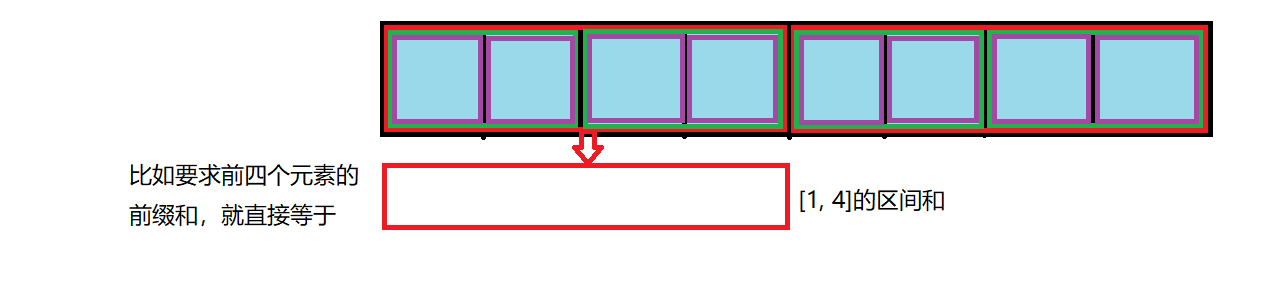
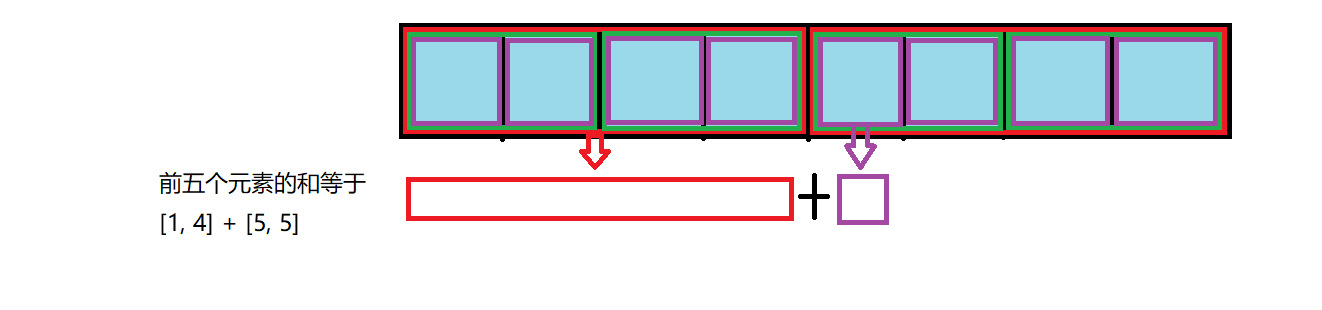
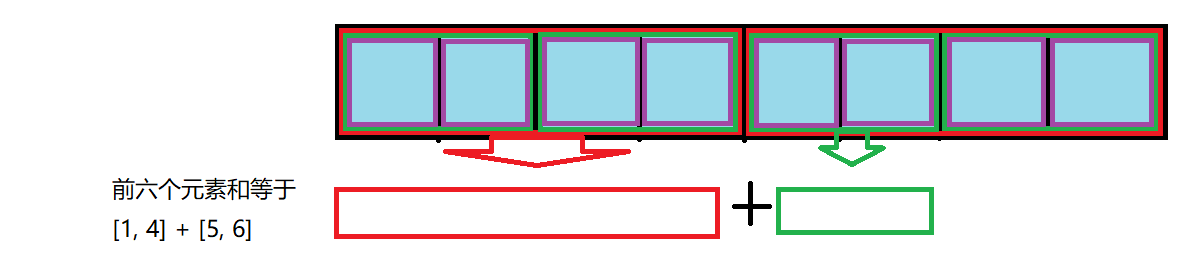
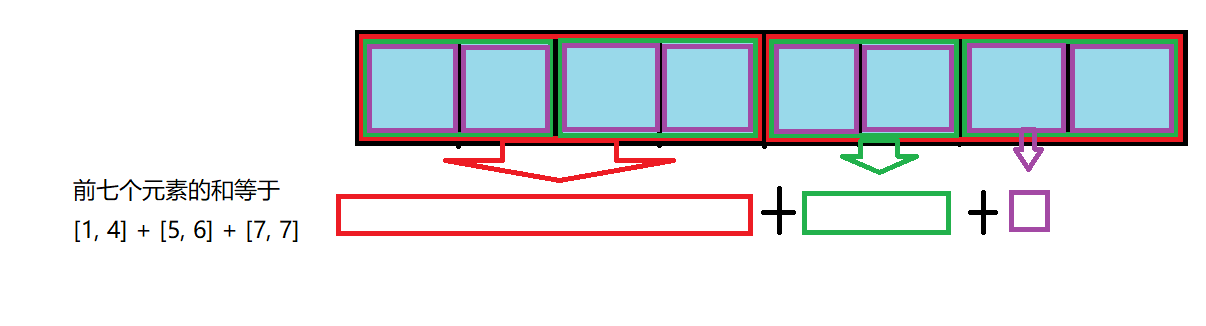

从这些图中我们可以看出每次的询问的复杂度都是O(logn),然后修改的话,由于每个元素就只涉及包含它的那个区间部分,二分下来也就最多有logn个,所以这里的单点修改复杂度也是O(logn),虽然询问的复杂度提高了,但是修改的复杂度大大下降,总体来说算法还是变得高效了的。
也就是说,实际上我们是在建一颗树,然后这些树的结点都是存着区间和的,而修改某个结点不过是顺着叶子结点摸到祖先修改一遍而已.......嗯?等等!这不就是线段树么!
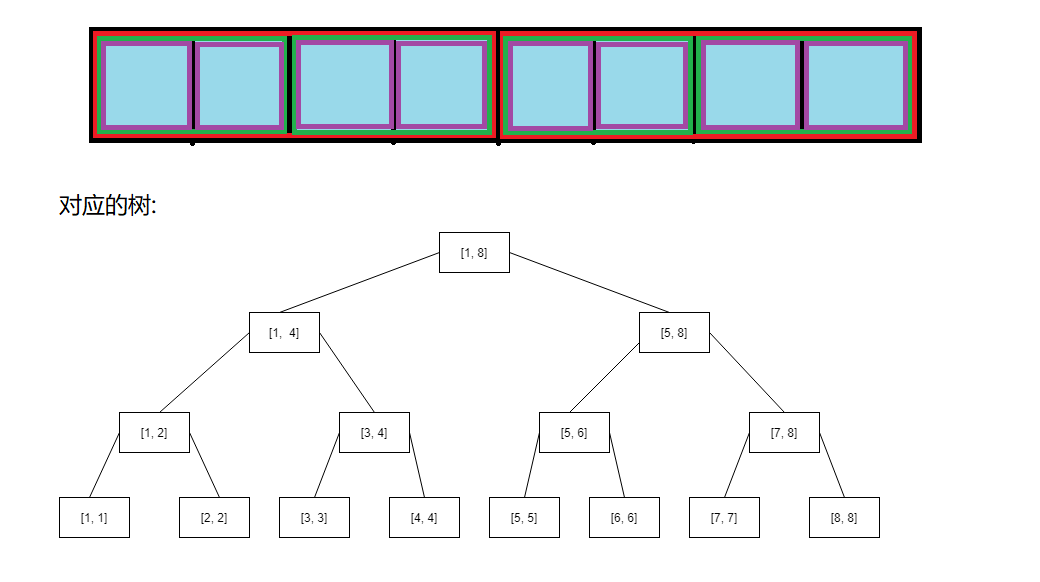
嗯,没错,就是线段树,还是那种不需要tag的,只支持单点修改的线段树。
虽然得到了O(logn)的修改跟查询前缀和的方法,但是你仍然没有停止你的研究,因为线段树是本来用于区间修改跟区间查询的,这样用于简单的单点修改以及前缀和询问中是不是有点大材小用了。。。而且像[2, 2]、[4, 4]、[6, 6]这些作为右孩子的叶子结点根本就是没用的,浪费掉了,你心里总觉得有点不自在,又想着有没有更好的办法
于是你把目光重新看向了这颗线段树,看看在单纯的单点修改以及求前缀和情况下的线段树会有什么特点,然后利用这些特点去简化运算。
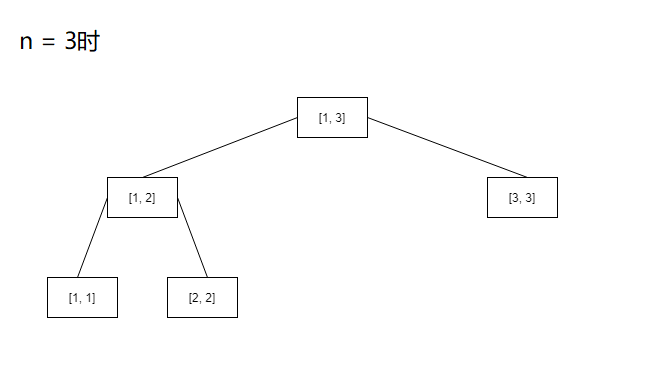
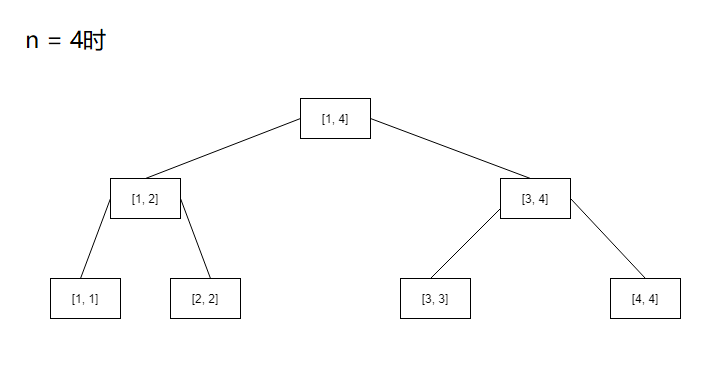
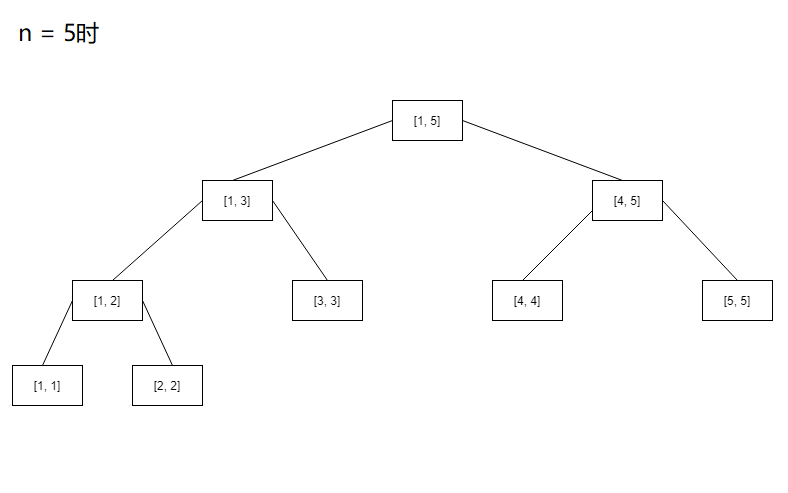
先想想n取不同时线段树的情况


。。。
咋看之下杂乱无章,但是突然这其中有几个完美得突出的线段树引起了你的注意,就是n = 2, 4, 8等等这些n等于二次幂时的树
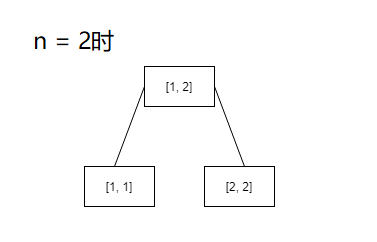
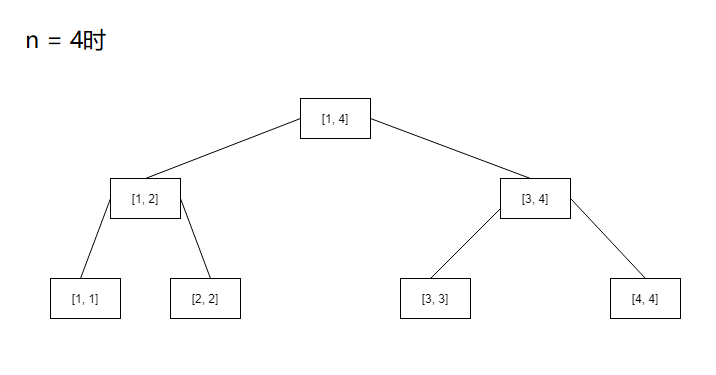
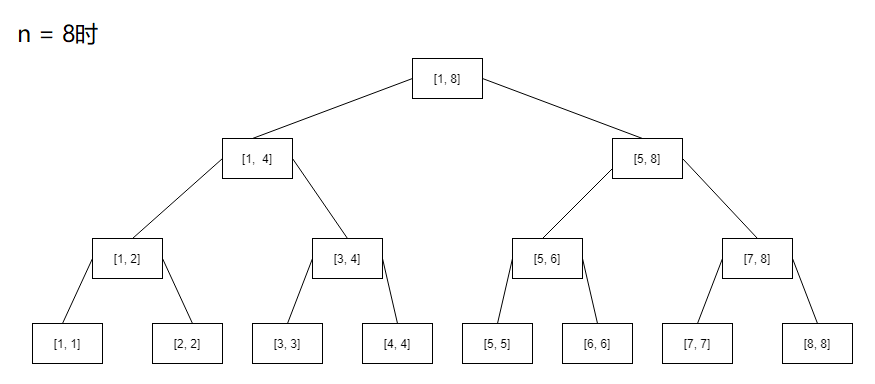
你发现这些都是满二叉树,而且幂次比较低的树会成为幂次比较高的左子树
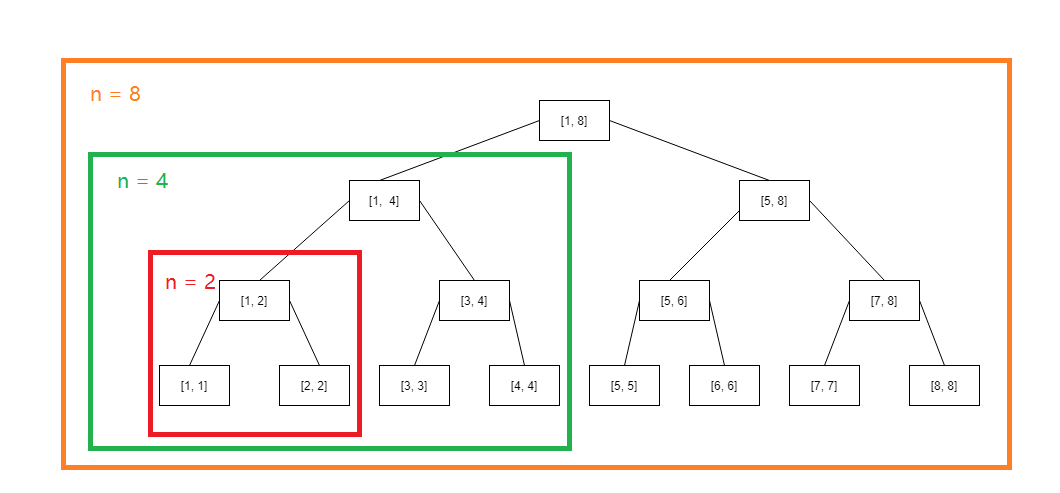
这个发现可不得了!这意味着对于所有的n都能用一种统一的线段树结构去表示!就是满二叉树。对于n不等于2的幂次的情况,也是可以用比n大的最近的2的幂次的数(比如比7大的最近的2的幂次的数是8)作为根然后进行扩展去照样构建一个满二叉树的,只是实际求和的时候包含了比n大的数的结点不会被访问而已,下图是n = 7的情形
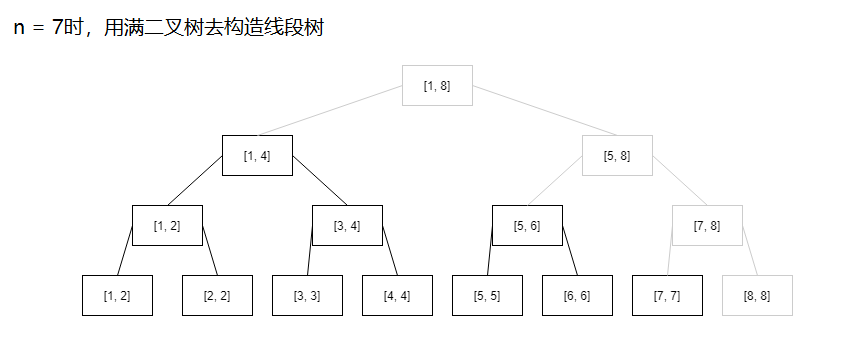
灰色部分是扩展出来的结点,也就是说7是先扩展成了8然后再建树的,但是实际上有数值的只有黑色部分结点,那么这种情况下比如求前七项的前缀和的话那就是[1, 4]+[5, 6]+[7, 7]
怎么从一个单纯的数字7从这棵树找到[1, 4]、[5, 6]、[7, 7]这三个结点呢?
观察上图可以知道,从7先找到大于等于7又离7最近的2次幂数也就是8,然后从[1, 8]结点开始往下找,碰到结点区间的右端点小于等于7的就直接返回结点数值作为前缀和的一部分。
这似乎只涉及了区间右端点。。。
于是你把区间左端点给抹去了,看对运算有没有影响
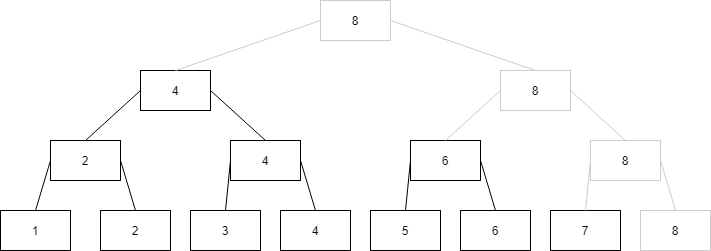
然后你发现结点跟右孩子竟然惊人地相似!
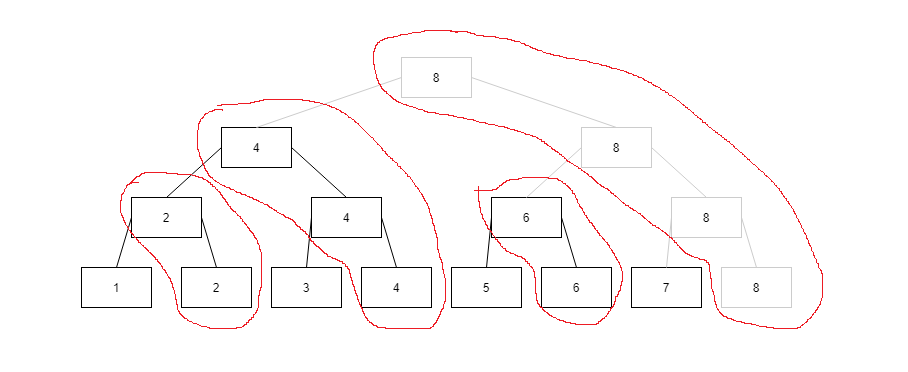
求7的前缀和,实际上就是从7先找到最上面的8
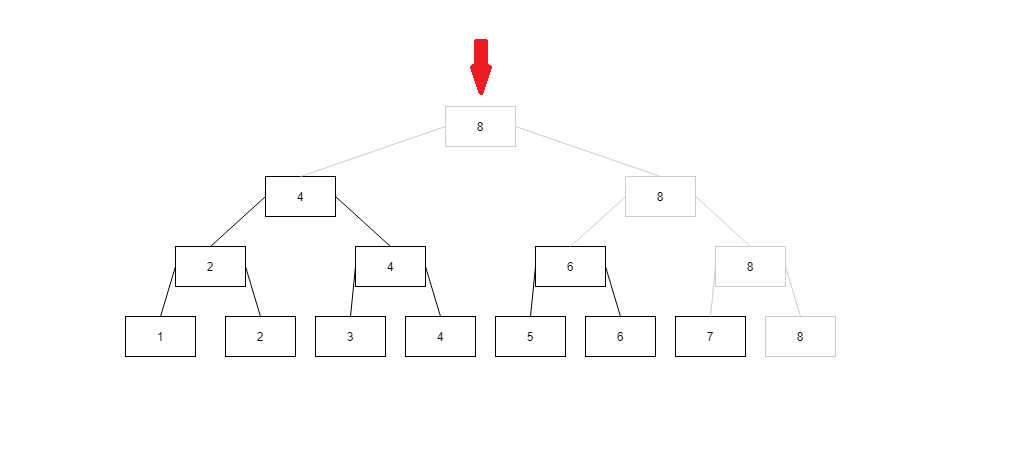
然后8大于7,不能直接用于求和,箭头往左摸摸到了4
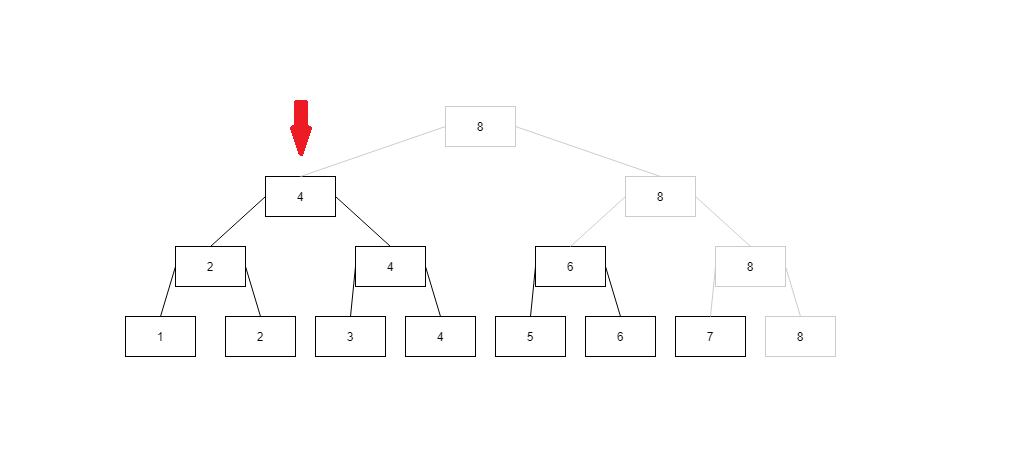
4小于等于7了,就直接用于求和,但是[5, 7]部分我们还没有覆盖,又知道8比7大,那么就忽略所有8的结点,这样往右摸比4大的结点,就摸到了6
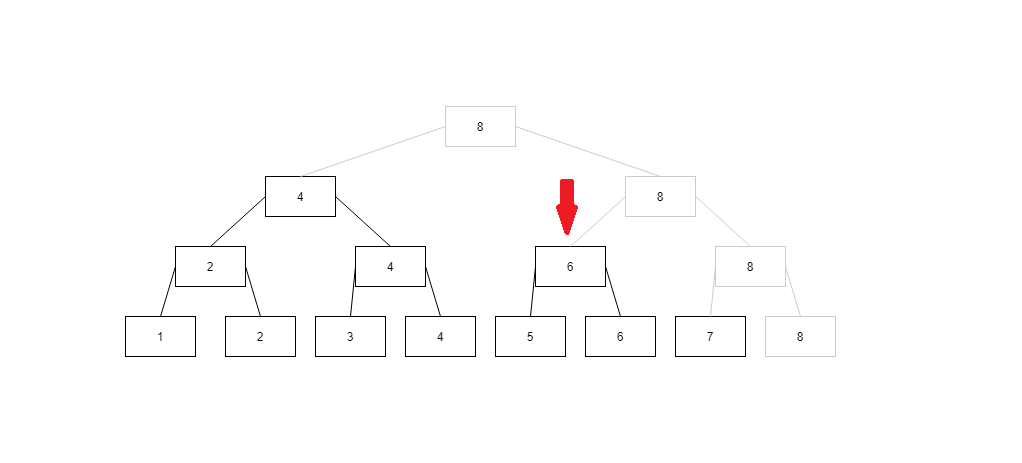
然后6小于等于7了,这个箭头所指结点的值就作为求和一部分,然后我们还缺[7, 7]的值,就用同样方法往右摸,就摸到了7
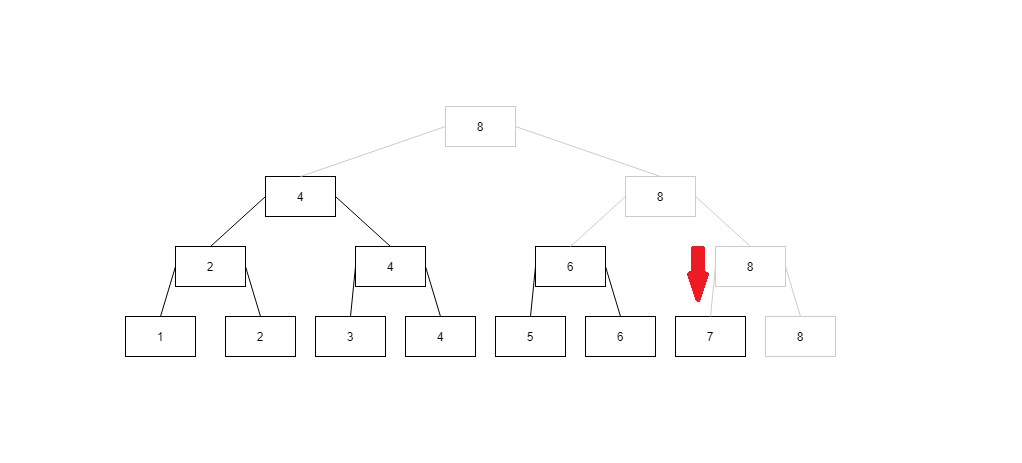
7摸完之后[1, 7]区间就被完全覆盖了,求前缀和的过程就完成了
至于忽略结点的方法,你想到了一个好主意
8搜完后如果往下搜,那肯定就是直接搜4, 6, 7了,根结点之外的8都是冗余的,全改接根结点
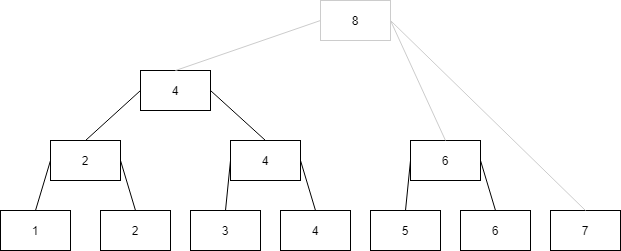
这样,当发现8大于7之后就能很自然地往下搜4、6、7了
然后,你发现其他结点的右孩子也能这样去除冗余,这么做之后你发现树变成了这样
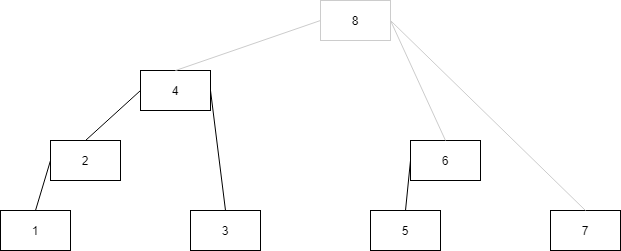
树变得非常干净呀,就1~8一个个地排在那,用长度为2^k(2^k为大于等于n的离n最近的二次幂数)的数组就能存下这棵树,但因为扩展出来的结点没有实际数值在里边,所以用长度为n的数组其实也能存的下,表面上看,他们之间就只存在管辖关系了,这样子从空间上,你把线段树又给优化了一遍。
然后你的研究问题就转化成了研究这些数之间的管辖关系
先回到查询前缀和的情形,这任务现在已经变成了给一个数x,然后怎么迅速定位到小于等于x的所有节点所构成的森林当中的每一棵树的根结点
比如查询5,那么小于等于5的结点有1、2、3、4、5,这些结点构成的森林共有2颗树,其中一颗根结点为4,另一颗根结点为5,而这两个根结点就是你所需要的东西
怎么去定位呢?那得先想想随便给个数,怎么确定这个数所对应的森林确定了几棵树,1、2、4、8都是1棵,3、5、6都是2棵,而7有3棵,只有1棵树的数的规律好找,就是都是2的k次幂的数,但是2棵、3棵甚至更多棵的怎么去解释呢?
又是二分又是和2的k次幂密切相关的,直觉上你觉得这个可能跟数的二进制表示有关系,于是你试着把结点的数全部用二进制表示试试
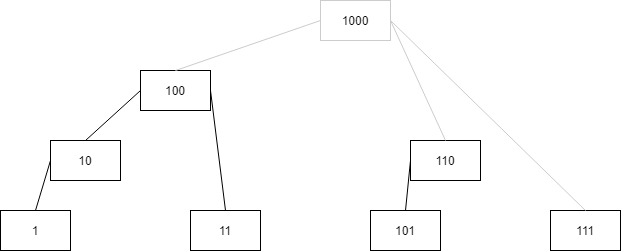
嗯?这么一试好像还真试出了点东西,从表面上看,似乎二进制表示有几个1就表示这个数对应的森林有几棵树,二进制的低位1后面有几个0就表示这个数所表示的结点直接管辖了几个结点。
为什么会这样?偶然吗?还是说有它的道理的?本着刨根问底的精神,你深入去研究了
首先看看10管辖的1是怎么来的,我们知道去除冗余之前本来结构是这样的
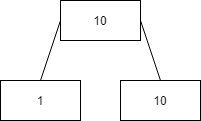
这时候我们还想不到什么管辖关系,有的只是查找关系,但是去除冗余之后

作为叶子结点的10就消失了,结果上就是1被10管辖了
从以前的满二叉树来看
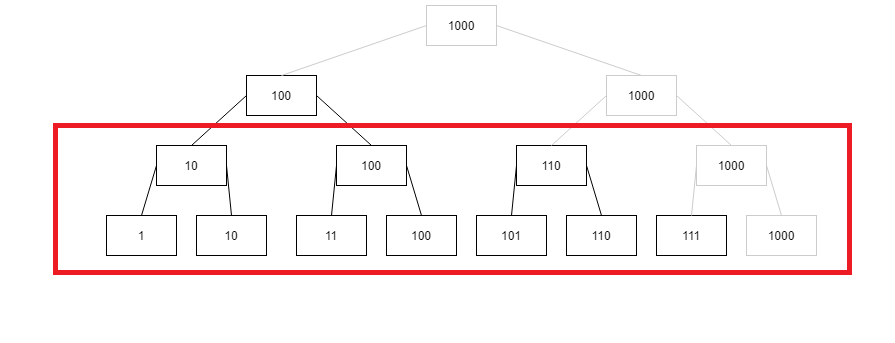
满二叉树的叶子都是1和2,3和4,5和6这样子搭配然后往上形成树,形成树的父节点的标签就是右孩子的标签,也就是2、4、6这些2的倍数,映射到二进制表示就是最低位为0的数,相应的父节点的右孩子就要删去以去除冗余,这样原本的右孩子所对应的数就成为了管理者,所以10管辖着1、100管辖着11、110管辖着101等可以说是当然的结果。
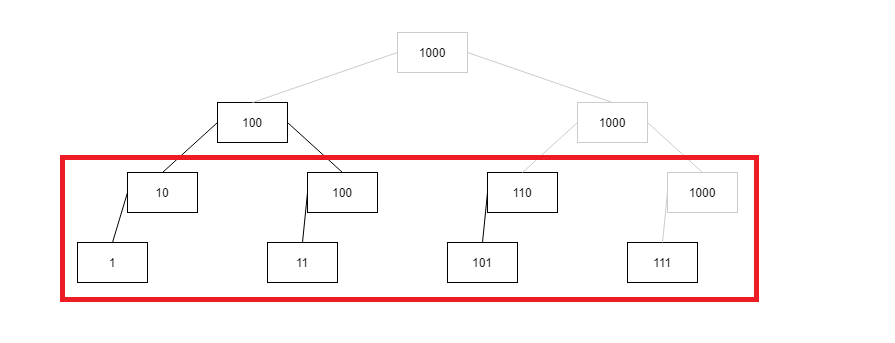
然后观察第2层
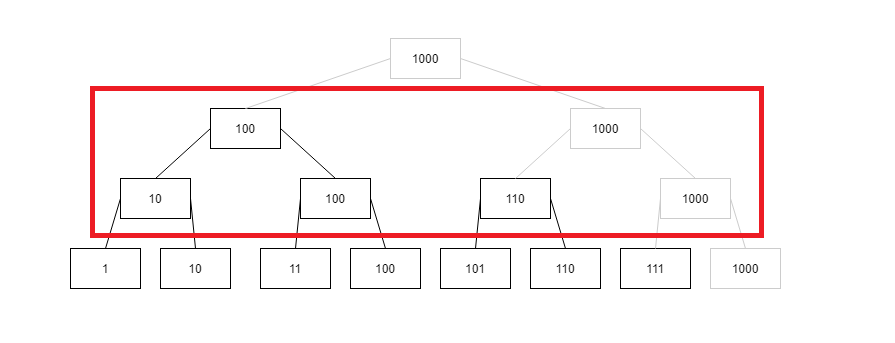
不难看出这次成为管理者的是100和1000,为什么会是它们?因为他们经过第一层的上升之后,又成为了右孩子,那么成为第二层的右孩子的条件是什么?第一层要作为右孩子,就是从左往右数,每第二个数就是右孩子,结果上来看就是2的倍数成了右孩子,然后成为第二层的右孩子的条件就是在第二层中从左往右数每第2个就是右孩子,反映到第一层中就是从左往右数每第4个数成为了第二层的右孩子,也就是4的倍数成为了右孩子,之后我们也不难推出第三层成为右孩子的会是第一层中从左往右数的每第8个数,也就是8的倍数会成为第三层的右孩子
那么最终演变结果就是,一个数所在结点会直接管辖着几个结点,会取决于这个数可以与2的几次幂整除,反映到二进制表示上,就是取决于这个数从最低位的1的再往低有几个0,这个数所在结点就直接管辖了几个结点
然后具体直接管的哪几个结点,用与上边类似的方法,可以推知,设一个数为x,那么小于x的数当中如果有是这个数的本身加上这个数的最低位的1就能等于数x的,那么这个数所在结点就是归x所在结点直接管辖,比如10加上最低位的1后就变成了100,所以10归100直接管辖,101加上最低位的1后就变成了110,所以101归110直接管辖,而110加上最低位的1后就变成了1000,所以110归1000直接管辖。反过来我们也能知道一个数会被哪个数直接管辖,推算直接管辖1010的数,我们就把1010 + 10得到1100,这就是直接管辖1010的数。
知道这些管辖关系,至少我们得到了这种简化线段树的修改方法,修改单个点x,无非就是从x所对应的结点开始顺着管辖关系往上更新即可。
你知道有个神奇的算法叫lowbit,能直接找到一个数x的最低位的1,因此在这个修改算法中“往上摸”就是x迭代加上lowbit就是。
int lowbit(int x) { return x & -x; }
void add(int n, int x, int k) { while (x <= n) { c[x] += k; x += lowbit(x); } }
而建树,实质上不就是一开始树中的数据都是0,然后有n个单点修改么
void BuildTree(int n) { for (int i = 1; i <= n; i++) add(n, i, a[i]); }
但是这时候仍然没找到具体的简化线段树的查询方法,就是给出一个数x,然后拿着这个数x找到小于等于它的所有数所在结点所构成森林中的每棵树的根结点。
不管怎么说给出一个数x,虽然还不清楚x对应森林的所有树的根结点,但至少x数本身所在的结点就是其中之一。然后这个x数本身所在结点直接跟间接所管辖的所有结点覆盖了哪些区间呢?通过上面的管辖关系可以推知,一个数x减去最低位的1再加上一个普通的1要么直接被x所在结点直接管辖,要么就是被间接管辖,从1100这个数来说,这个数减去最低位的1后就是1000,然后加上一个普通的1就是1001,这个1001被1010直接管辖,然后1010被1100直接管辖,总的来说1001是被1100间接管辖的,如果1000没有加上普通的1,那么1000是没有被1100管辖的。1001被管辖了,1001到1100都是归1100所在的结点直接或间接管辖,也就是说这就推出了数x所在结点的管辖范围,然后也可以推算出x-lowbit(x)就是管辖范围之外的最大的数了,x-lowbit(x)这个数重复上述过程又能得到更小的管辖范围外最大的数,减到数为0了,那么从1到x就正好被全部覆盖了,而且这些覆盖是没有重叠的,具体这个过程要重复几次呢?答案就是数x有几个1就重复几次,因为每次都减去最低位的1,就一共能减这么多次。这就是这种线段树的查询方法了。
int get_sum(int n, int x) { int res = 0; while (x) { res += c[x]; x -= lowbit(x); } return res; }
至此,你研究出了一种用简化的线段树去存区间和的方法,使用的空间为O(n),然后区间和询问跟单点修改的复杂度都是O(logn),算是相当不错的算法了,你觉得研究到这个地步应该也差不多了,这个问题就此告一段落。
后来,人们把这个简化的线段树叫做binary indexed tree,二进制编码树,也就是我们今天所熟悉的树状数组。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号