概率dp学习记录
论文参考 汤可因《浅谈一类数学期望问题的解决方法》
反正是很神奇的东西吧。。我脑子不好不是很能想得到。
bzoj 1415
1415: [Noi2005]聪聪和可可
Time Limit: 10 Sec Memory Limit: 162 MBSubmit: 2140 Solved: 1258
[Submit][Status][Discuss]
Description
Input
数据的第1行为两个整数N和E，以空格分隔，分别表示森林中的景点数和连接相邻景点的路的条数。 第2行包含两个整数C和M，以空格分隔，分别表示初始时聪聪和可可所在的景点的编号。 接下来E行，每行两个整数，第i+2行的两个整数Ai和Bi表示景点Ai和景点Bi之间有一条路。 所有的路都是无向的，即：如果能从A走到B，就可以从B走到A。 输入保证任何两个景点之间不会有多于一条路直接相连，且聪聪和可可之间必有路直接或间接的相连。
Output
输出1个实数，四舍五入保留三位小数，表示平均多少个时间单位后聪聪会把可可吃掉。
Sample Input
【输入样例1】
4 3
1 4
1 2
2 3
3 4
【输入样例2】
9 9
9 3
1 2
2 3
3 4
4 5
3 6
4 6
4 7
7 8
8 9
4 3
1 4
1 2
2 3
3 4
【输入样例2】
9 9
9 3
1 2
2 3
3 4
4 5
3 6
4 6
4 7
7 8
8 9
Sample Output
【输出样例1】
1.500
【输出样例2】
2.167
1.500
【输出样例2】
2.167
论文题。。自己看看论文就懂了。
1 #include<bits/stdc++.h> 2 #define clr(x) memset(x,0,sizeof(x)) 3 #define clr_1(x) memset(x,-1,sizeof(x)) 4 #define INF 0x3f3f3f3f 5 #define mod 1000000009 6 #define LL long long 7 #define next nexted 8 using namespace std; 9 const int N=1e3+10; 10 int ans[N][N],vis[N],step[N][N]; 11 double f[N][N]; 12 int u,v,m,n,pu,pv; 13 vector<int> edge[N]; 14 void bfs(int root) 15 { 16 int now,p; 17 clr(vis); 18 queue<int> que; 19 step[root][root]=root; 20 vis[root]=1; 21 for(int i=0;i<edge[root].size();i++) 22 { 23 p=edge[root][i]; 24 que.push(p); 25 step[root][p]=p; 26 vis[p]=1; 27 } 28 while(!que.empty()) 29 { 30 now=que.front(); 31 que.pop(); 32 for(int i=0;i<edge[now].size();i++) 33 { 34 p=edge[now][i]; 35 if(!vis[p]) 36 { 37 que.push(p); 38 vis[p]=1; 39 step[root][p]=step[root][now]; 40 } 41 } 42 } 43 return ; 44 } 45 double Find(int u,int v) 46 { 47 if(u==v) 48 return f[u][v]=0; 49 if(f[u][v]>0) 50 return f[u][v]; 51 if(step[u][v]==v) 52 return f[u][v]=1; 53 if(step[step[u][v]][v]==v) 54 return f[u][v]=1; 55 int p; 56 for(int i=0;i<edge[v].size();i++) 57 { 58 p=edge[v][i]; 59 f[u][v]+=Find(step[step[u][v]][v],p); 60 } 61 f[u][v]+=Find(step[step[u][v]][v],v); 62 f[u][v]=f[u][v]/(edge[v].size()+1)+1; 63 return f[u][v]; 64 } 65 int main() 66 { 67 scanf("%d%d",&n,&m); 68 scanf("%d%d",&u,&v); 69 for(int i=1;i<=m;i++) 70 { 71 scanf("%d%d",&pu,&pv); 72 edge[pu].push_back(pv); 73 edge[pv].push_back(pu); 74 } 75 for(int i=1;i<=n;i++) 76 sort(edge[i].begin(),edge[i].end()); 77 for(int i=1;i<=n;i++) 78 bfs(i); 79 printf("%.3f\n",Find(u,v)); 80 return 0; 81 }
bzoj 2685
2685: Sgu385 highlander
Time Limit: 10 Sec Memory Limit: 128 MBSec Special JudgeSubmit: 112 Solved: 64
[Submit][Status][Discuss]
Description
一个游戏N个人，每个人开始一张卡片，上面写着N个人中某个人的名字。
每张卡片上的名字都不同，且不会拿到自己名字的卡片。
游戏开始时，每个人开始追自己卡片上写着的人，如果A有写着B的卡片。
当A追到B后，A可以拿到所有B的卡片。如果每个人都没人可追，游戏结束。
这时开始数每个人手上的卡片总数，获得卡片最多的人即是胜者。如果有多个人
的卡片一样多，则都是胜者。现想知道有多少人在理论上有概论成为胜者。
Input
输入一个整数N ２<=N<=100
Output
一个实数
Sample Input
2
Sample Output
2
HINT
你的答案与标准答案的差不超过10^-9
Source
同样的一道论文题。
这个题目我们可以把这些错排看成一张有向图。由于每个点出入度为1，且不会指向自己。所以这是一个多个不相交的环，并且不存在自环（这个很重要，公式推导的时候环长度>1）组成的图。
那我们看看数据范围n≤100，所以能接受O(n3)的算法。
于是我们做这么一个三维的推导：
f[i][j][k]代表有i个点确定，其中最长的环长度为j，且长度为j的环数量为k的情况数量，K也为获胜人数。
如果我们只形成一个长度为j的环，他的情况数量为A(n,j)/j，n为剩余点的数量。
如果我们k个长度为j的环，他的情况数量为(A(n,j)*A(n-j,j)*A(n-2*j,j)……A(n-(k-1)*j,j))/A(j,j)，n为剩余点数量。因为A(j,j)==j!==1*2*3……*j，所以我们从k=1推到k=n的时候f[i][j][k]=f[i-j][j][k-1]*A(n-(i-j),j)/j。
然后g[i][j]代表i个点确定，最长环长度为j的情况数量，即把k那一维求和。
可得出以下公式：
答案分母为情况总数，即错排总数，可以通过错排递推式得到：
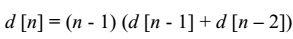
他是所有和项的分母。他和上面的j*f[i][j][k]形成每种获胜人数下的权（概率）。
然后j*k是每种情况的下获胜人数，就是环里所有人都可能赢，没毛病。
相当于运用全概率公式E(K)=E(E(K|J)=|J=1)+E(K|J=2)……E(K|J=n)
1 #include<bits/stdc++.h> 2 #define clr(x) memset(x,0,sizeof(x)) 3 #define clr_1(x) memset(x,-1,sizeof(x)) 4 #define mod 1000000007 5 #define LL long long 6 #define INF 0x3f3f3f3f 7 using namespace std; 8 const int N=1e2+10; 9 double f[N][N][N],g[N][N]; 10 double pre[3],ans; 11 double jc[N]; 12 int n,m,T,p; 13 double a(int n,int m) 14 { 15 return n>=m?jc[n]/jc[n-m]:0; 16 } 17 int main() 18 { 19 scanf("%d",&n); 20 pre[0]=pre[1]=0; 21 pre[2]=1; 22 for(int i=3;i<=n;i++) 23 pre[i%3]=(i-1)*(pre[(i-1)%3]+pre[(i-2)%3]); 24 jc[0]=jc[1]=1; 25 for(int i=1;i<=n;i++) 26 jc[i]=jc[i-1]*i; 27 for(int i=2;i<=n;i++) 28 { 29 for(int j=2;j<i;j++) 30 { 31 p=min(i-j,j-1); 32 for(int k=2;k<=p;k++) 33 f[i][j][1]+=g[i-j][k]; 34 f[i][j][1]*=a(n-i+j,j)/j; 35 g[i][j]=f[i][j][1]; 36 p=i/j; 37 for(int k=2;k<=p;k++) 38 g[i][j]+=(f[i][j][k]=f[i-j][j][k-1]*a(n-i+j,j)/j/k); 39 } 40 f[i][i][1]=g[i][i]=a(n,i)/i; 41 } 42 for(int i=2;i<=n;i++) 43 { 44 p=n/i; 45 for(int j=1;j<=p;j++) 46 ans+=f[n][i][j]*j*i; 47 } 48 ans/=pre[n%3]; 49 printf("%.10f\n",ans); 50 }
bzoj 1419
1419: Red is good
Time Limit: 10 Sec Memory Limit: 64 MBSubmit: 1210 Solved: 560
[Submit][Status][Discuss]
Description
桌面上有R张红牌和B张黑牌，随机打乱顺序后放在桌面上，开始一张一张地翻牌，翻到红牌得到1美元，黑牌则付
出1美元。可以随时停止翻牌，在最优策略下平均能得到多少钱。
Input
一行输入两个数R,B,其值在0到5000之间
Output
在最优策略下平均能得到多少钱。
Sample Input
5 1
Sample Output
4.166666
HINT
输出答案时,小数点后第六位后的全部去掉,不要四舍五入.
Source
这个人的决策只有两种：翻开牌和不翻开牌。所谓的最优策略。。还有什么最优?当然是期望得到的钱最优啊。因此在I张R和J张B的情况下，如果我们翻牌的期望>0也就是还能拿钱的情况下我们选择继续翻牌来获得金钱。反之不翻牌，期望为0。
设f[i,j]表示还剩I张R牌和J张B牌的期望，边界条件是f[i,0]=f[i-1,0]+1,f[0,j]=0。转移方程是$f[i][j]=(f[i-1][j]+1)*\frac{i}{i+j}+(f[i][j-1]-1)*\frac{j}{i+j}$。
1 #include<bits/stdc++.h> 2 #define clr(x) memset(x,0,sizeof(x)) 3 #define clr_1(x) memset(x,-1,sizeof(x)) 4 #define mod 1000000007 5 #define LL long long 6 #define INF 0x3f3f3f3f 7 using namespace std; 8 const int N=5e3+10; 9 int n,m; 10 double f[2][N]; 11 int main() 12 { 13 scanf("%d%d",&n,&m); 14 for(int i=1;i<=n;i++) 15 { 16 f[i&1][0]=f[i&1^1][0]+1; 17 for(int j=1;j<=m;j++) 18 f[i&1][j]=max(0.0,((f[i&1][j-1]-1)*j+(f[i&1^1][j]+1)*i)/(i+j)); 19 } 20 printf("%.6f\n",((LL)(f[n&1][m]*1000000))*1.0/1000000); 21 }
