莫比乌斯反演

 

     在acm-icpc程序设计系列上这一块基本是点到即止，只给了公式和几个简单例子，没怎么给应用。而网上复制黏贴的居多，都是难以理解的博客内容。功夫不负有心人，终于找到一个尽心尽责的博客：

http://blog.sina.com.cn/s/blog_76f6777d0101bi0z.html（参考一部分）　

　　这个反演放在容斥定理这一块是有一定道理的，它是偏序集的容斥定理公式延伸出来的东西。

　　废话不多说，开始数学玄学的探索。

     first 

　　首先是偏序集的容斥定理公式：

　　

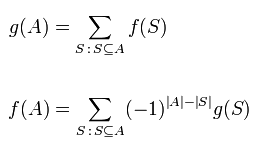
    这个公式即对于偏序集<A,<=>有运算g(A),他由A的所有子集S作f(s）运算而得(假设g(x)已知f(x)未知），那么f(A)即为对所有s作g(x)运算并乘以(-1)^(|A|-|S|))(|A|为A集合中元素个数.基数）的和，反演推理出f(x)的值。当g(x)=|x|时，就类似于容斥原理了。只不过容斥原理是几个子集Pi且Pi的交集为A，而这是A的所有子集。

　　下面给出证明，参考该博客的公式证明：

　　

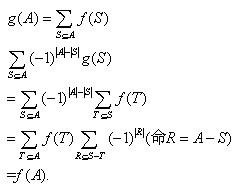
　　【注意 第四行 R 属于 S-T 其实应该是  R属于 A-T.. 懒得改了..】

　　3—>4:3 是将所有包含于s的T进行了f运算然后乘p=(-1)^|R|再将所有按照各s进行求和，四则是把上面的运算顺序调换，对于每个，T先将T被包含于的S进行|R|=|A-S|求和，然后在把答案乘f(T）按照各T进行求和。

     

　　4->5 ：

　　　　当T=A,即A-T为空集时，R只能为空集，sigma (-1)^|R| =1,  即 f(T=A) 在式子中被累加一次.

　　　　当T！=A时，即A-T为非空集，把每个|R|=k的(k 属于 [0,|A-T|])放到一起算..有 :

　　　　Σ[R属于A-T](-1)^|R|= Σc(|A-T|,k)*(-1)^k =（1-1)^|A-T|=0..由二项式定理得 =0 . 所以这些f(T!=A) 均不被累加.

　　　　 所以化成了第5行.

 　　second

　　接下来就是莫比乌斯反演了：　　

    由于类似整除关系是满足是偏序关系..所以也可以用上述容斥原理..

先是公式（数用大写表示不大适合的样子..但为了与上面的对应..恩)

g(A)=sigma[S|A] f(S)

f(A)=sigma [S|A] miu(A/S) * g(S)

    把 a|b看做 a属于b，a-b看成a/b,a+b(a并b)看成a*b，其实就一样了..

miu(d)的取值，可以用容斥原理来理解.. 写一下f(60)什么的会发现..这里的减少一个元素的子集，就是剔除一个质因数，然后因为就算的时候不会重，所以第一次时剔除的质因数不会相同，那么后面所构成的数（也就是前面所构成的并），分解质因数后，也不会有质因数相同.

    或者我们用上面证明极类似的方法.. 可以顺便说明 miu(d)的取值 :

sigma [S|A] miu(A/S) * g(S)=sigma[T|A]( f(T) * sigma[S|A,T|S] miu(A/S) )

    现在要使:

T=A时， 后面的sigma=1，由于此时只有 T=S=A, 所以sigma=1=miu(A/S)=miu(1) ，即miu(1)=1

T!=A时，与上面类似的构造R=A/S，R| (A/T) ，对于每个R,有S=A/R 一 一对应，且 必有 T|S，式子化成了

sigma [T|A] f(T)*sigma[R|(A/T)] miu(R)

由于T|A,T!=A, 首先 (A\T) >1 .. 要尽量在满足这个的情况下，使这个=0. miu(R)也是类似等于|R|,即R包含的元素个数. 元素个数具体是什么? 首先，由于上面的每个元素是视作不同的，才可以直接用c(,)而不去重.. 而如果有重的，这里式子中实际只会算一次，所以 这些元素是要不一样的.. 

->想到 若 d=p1p2..pn且每个质因数恰一个的情况下，miu(d)= (-1)^n . 其他情况除了miu(1)=1,都为0

   若此时 R=p1^x1 * p2^x2..* pm^xm，同样把取到的每个质因数只有一个的满足 d|R的d, 把 质因数个数为n的放一起算.. sigma[R|(A/T)] miu(R) = miu(1)+ sigma[1<=n<=m] c(m,n)*(-1)^n =0

就又有 原式=f(A)了..

　　

---

2016-09-16 21:38:46　

 时隔半年继续拾起当年的莫比乌斯反演。感谢贾志鹏大大的pdf让我看懂了莫比乌斯反演跟容斥原理的真正关系，以及一些函数用线性筛的快速求法：

【贾志鹏大大的pdf传送门】

下面是利用线性筛求一些函数从1-n的所有值得O(n)算法的模板：

#include<cstdio>
#include<iostream>
#include<cstring>
#define clr(x) memset(x,0,sizeof(x))
using namespace std;
int mu[100000];
int inf[100000];
int prime[100000];
int tot;
void  done(int n)
{
    clr(prime);
    clr(inf);
    clr(mu);
    mu[1]=1;
    tot=0;
    for(int i=2;i<=n;i++)
    {
        if(!inf[i])
        {
            prime[tot++]=i;
            inf[i]=1;
            mu[i]=-1;
        }
        for(int j=0;j<tot;j++)
        {
            if(i*prime[j]>n) break;
            inf[i*prime[j]]=1;
            if(i%prime[j]==0)
            {
                mu[i*prime[j]]=0;
                break;
            }
            else
            {
                mu[i*prime[j]]=-mu[i];
            }
        }
    }
    return ;
}
int main()
{
    int n;
    scanf("%d",&n);
    done(n);
    for(int i=1;i<=n;i++)
    {
        printf("%d ",mu[i]);
    }
    printf("\n");
    return 0;
}

#include<cstdio>
#include<iostream>
#include<cstring>
#define clr(x) memset(x,0,sizeof(x))
using namespace std;
int inf[100000];
int prime[100000];
int tot;
void  done(int n)
{
    clr(prime);
    clr(inf);
    tot=0;
    for(int i=2;i<=n;i++)
    {
        if(!inf[i])
        {
            prime[tot++]=i;
            inf[i]=1;
        }
        for(int j=0;j<tot;j++)
        {
            if(i*prime[j]>n) break;
            inf[i*prime[j]]=1;
            if(i%prime[j]==0)
                break;
        }
    }
    return ;
}
int main()
{
    int n;
    scanf("%d",&n);
    done(n);
    for(int i=0;i<tot;i++)
    {
        printf("%d ",prime[i]);
    }
    printf("\n");
    return 0;
}

#include<cstdio>
#include<iostream>
#include<cstring>
#define clr(x) memset(x,0,sizeof(x))
using namespace std;
int inf[100000];
int eu[100000];
int prime[100000];
int tot;
void  done(int n)
{
    clr(prime);
    clr(inf);
    tot=0;
    for(int i=2;i<=n;i++)
    {
        if(!inf[i])
        {
            prime[tot++]=i;
            inf[i]=1;
            eu[i]=i-1;
        }
        for(int j=0;j<tot;j++)
        {
            if(i*prime[j]>n) break;
            inf[i*prime[j]]=1;
            if(i%prime[j]==0)
            {
                eu[i*prime[j]]=eu[i]*prime[j];
                break;
            }
            else
                eu[i*prime[j]]=eu[i]*(prime[j]-1);
        }
    }
    return ;
}
int main()
{
    int n;
    scanf("%d",&n);
    done(n);
    for(int i=1;i<=n;i++)
    {
        printf("%d ",eu[i]);
    }
    printf("\n");
    return 0;
}