从贝壳看见宇宙:对数螺线主宰的一切
微信视频号:sph0RgSyDYV47z6
快手号:4874645212
抖音号:dy0so323fq2w
小红书号:95619019828
B站1:UID:3546863642871878
B站2:UID: 3546955410049087
造物主用数学语言,留下穿越时空的低语。
一个晴朗的午后,你走在海边,看到一个轮廓奇特的鹦鹉螺贝壳——
一个晴朗的午后,你走在海边,看到一个轮廓奇特的鹦鹉螺贝壳——

添加图片注释,不超过 140 字(可选)
聪明的你,很快注意到,这个螺旋般的轮廓线,似乎在哪见过?

添加图片注释,不超过 140 字(可选)
热带气旋/涡旋星系
从鹦鹉螺贝壳到涡旋星系,都隐藏一条神秘的曲线——对数螺线。为什么跨越微观与宏观、生物与非生物,都遵循相同的规律?
本文将从现象出发,揭示对数螺线的数学特征,并挖掘其物理学原理,最后探讨其哲学本质。全文约2,500字,对数理要求不高,欢迎食用。
01
复杂的简洁——对数螺线的数学特征
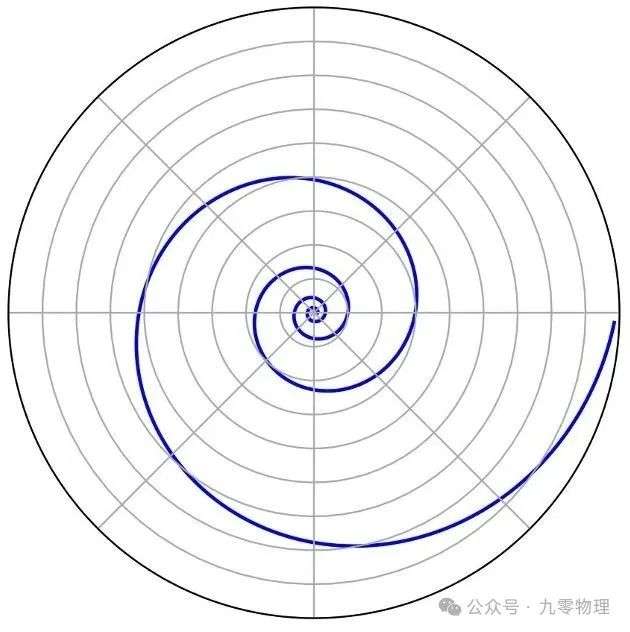
添加图片注释,不超过 140 字(可选)
让我们从某点(a,0)出发,沿着这条曲线,每经过一个点,记录一下两个信息:到原点的距离r,以及与原点的连线所转过的角度θ。
1638年,笛卡尔最早给出了这样的表达式:
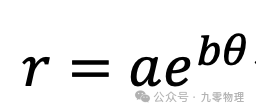
添加图片注释,不超过 140 字(可选)
转换一下,有
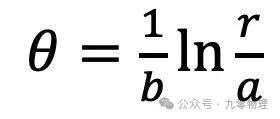
添加图片注释,不超过 140 字(可选)
即θ是关于r的对数函数,这也是对数螺线的名字由来。
添加图片注释,不超过 140 字(可选)
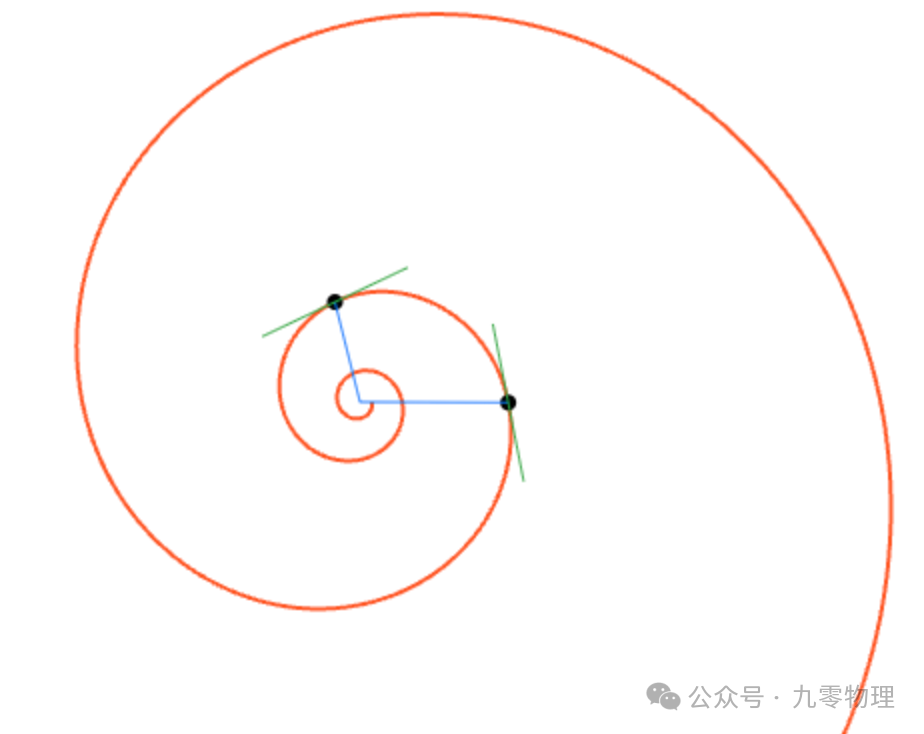
随后,雅各布·伯努利给出了这条曲线的一个神奇特性:每个点的切线与该点到原点的连线,成固定夹角,满足:
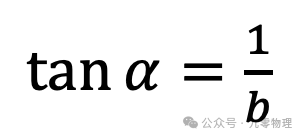
添加图片注释,不超过 140 字(可选)
所以,对数螺线也被称为等角螺线。
每个点的切线“角度”相等……那就意味着每个点存在某种“相似性”——
如果你截取对数螺线的某一段曲线,进行放缩、旋转,会发现跟其他某个区域的曲线会完全重合!
这在数学上叫“自相似性”。
如果让对数螺线“动”起来,它将重复自己的形状,从宇宙诞生到星辰湮灭……
这就是伯努利墓碑铭文“虽经改变,依然如故”(eadem mutata resurgo)。

添加图片注释,不超过 140 字(可选)
02
约束与优化
——对数螺线的物理学法则
为什么会有这样的数学特征——对数形式、等角性和自相似性?
我们尝试从物理学层面来揭秘,即对数螺线的生成过程受怎样的物理学法则所支配。
从一种简单情况开始。有四只小虫等距排列,如图所示,每只虫保持恒定速率运动,且方向始终朝着身旁的虫。问每只虫子的运动轨迹方程?
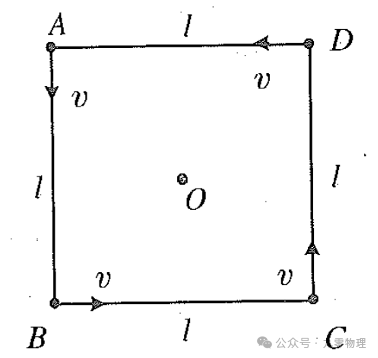
添加图片注释,不超过 140 字(可选)
根据对称性,任意时刻四虫连线依然成正方形,只是这个正方形在变化——旋转、缩小。
这个变化的正方形,保证每只虫的速度与到中心的连线的夹角不变!
由于速率恒定,所以每只虫径向速度大小不变,切向(垂直径向)速度大小也不变。
因此,每只虫的运动被一个条件所限定:径向速度与切向速度的比值保持不变。
这种运动产生的轨迹是对数螺线!
下面进行推导(可直接跳过)
(滑动以查看全文)
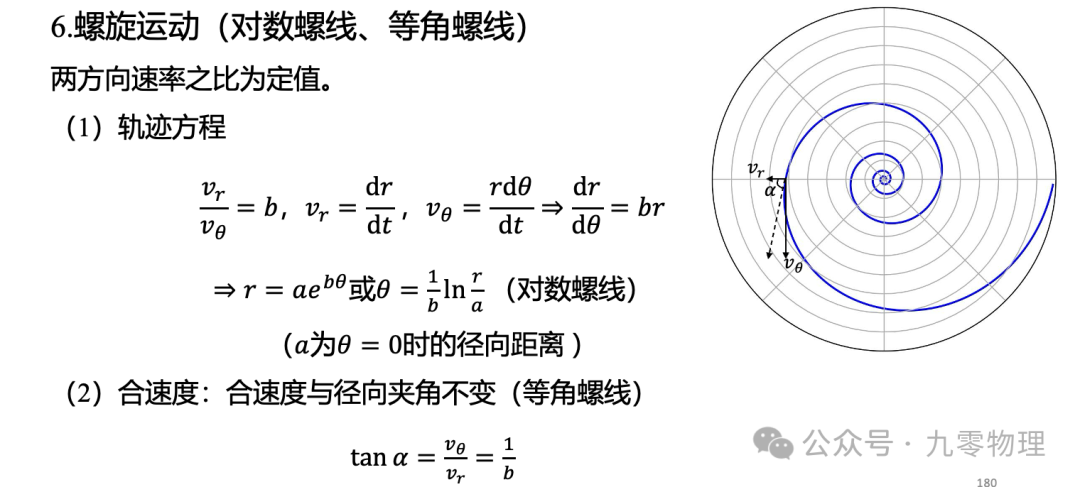
添加图片注释,不超过 140 字(可选)

添加图片注释,不超过 140 字(可选)
回到刚才的追逐问题,径向速度与切向速度的比值保持不变,会使运动轨迹为对数螺线。所以——
对数螺线是运动过程中速度分量之比保持恒定的产物。
比如热带气旋,这是气压梯度力、科里奥利力及惯性离心力共同作用下,径向速度分量与切向速度分量之比为(近似)定值的结果。
下面展开分析(可跳过)。
(滑动以查看全文)
想象一个水平放置的圆盘,你尝试从中心走向边缘。如果圆盘不转,你可以沿着一条半径直线抵达边缘。但如果圆盘转动起来(比如俯视逆时针旋转),你会受到一个垂直速度向右的力——科里奥利力,偏离原来的轨道。
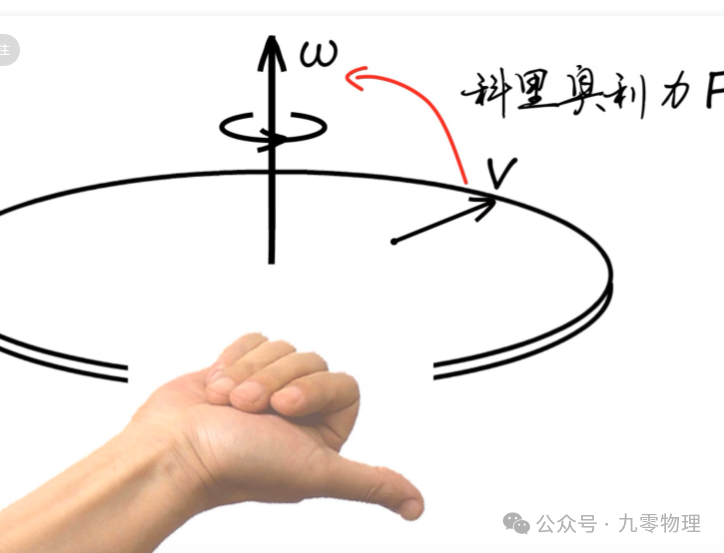
添加图片注释,不超过 140 字(可选)
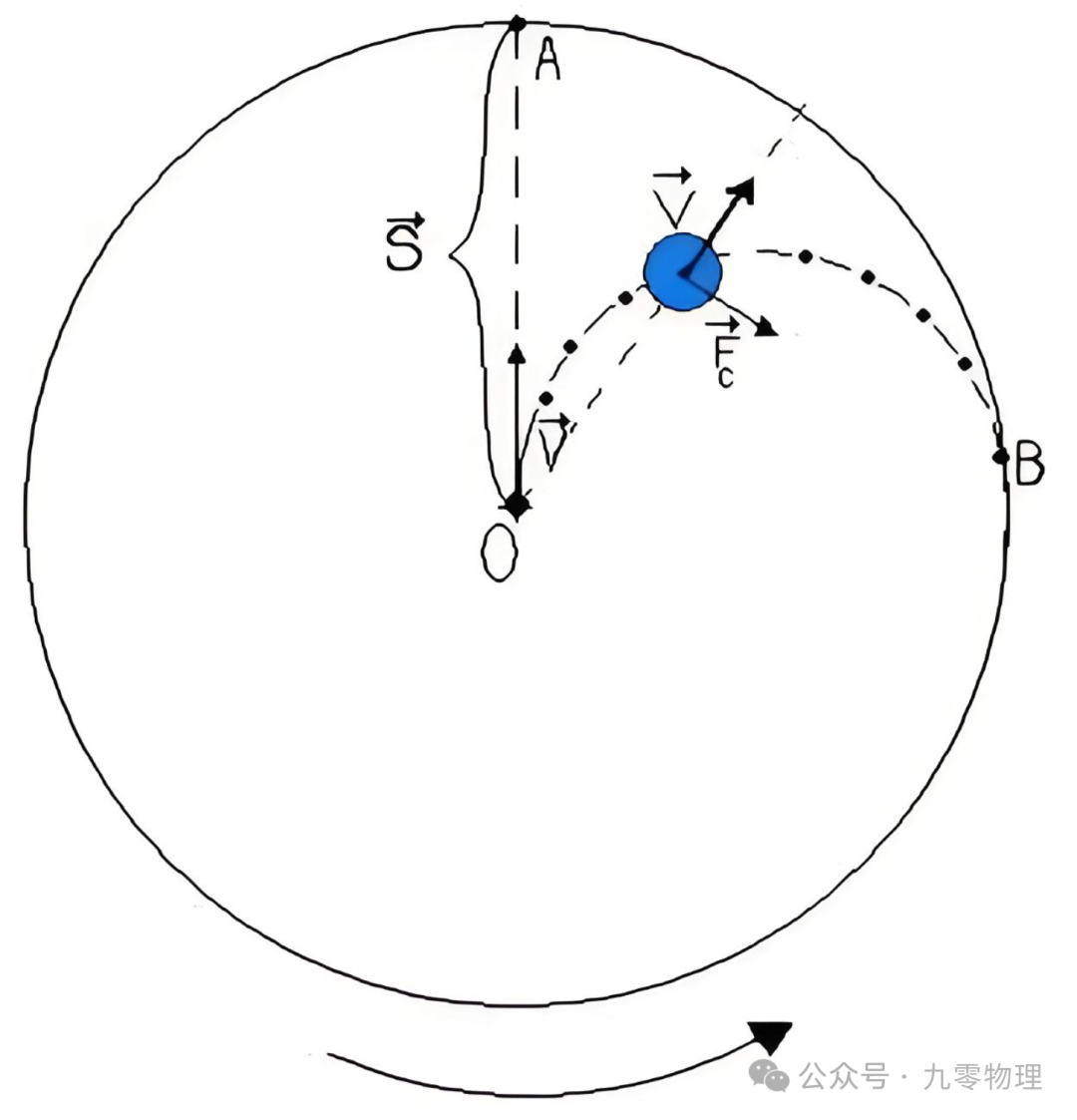
添加图片注释,不超过 140 字(可选)
现在想象一片赤道附近的低压区(高温形成)。由于气压差形成的压力——气压梯度力,会推动周围气团(北半球)向低压区运动(如同你从盘缘走向中心)。这时候地球的自转,会使得这团气受到垂直前进方向向右的力,向右前方偏转,形成螺旋云带。
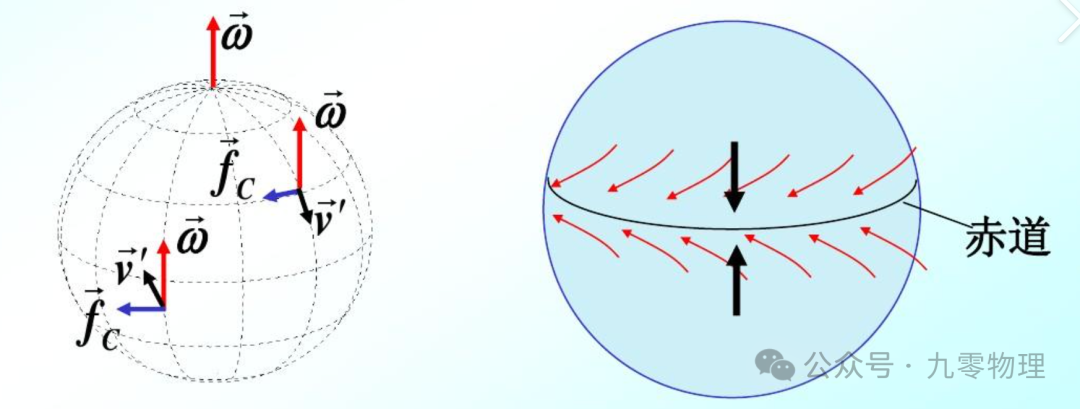
添加图片注释,不超过 140 字(可选)
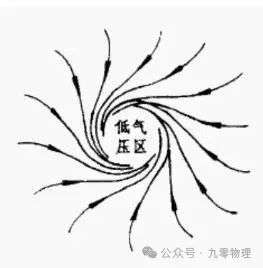
添加图片注释,不超过 140 字(可选)
随着气团越接近低压中心,三种力会达到平衡。质量守恒要求径向速度以1/r的方式增大,角动量守恒要求切向速度以1/r的方式增大,从而每时每刻径向速度与切向速度之比恒定。
也就是说,当一个结构在一方向的变化速率与另一方向的变化速率之比为定值,结构的形状会是对数螺线。
那我们很自然想问,为什么自然界会存在这种“变化速率之比恒定”的约束?
这是大自然在亿万年演化过程“发现”的最优方案——能量损耗最小、空间利用率最高、结构最强……
热带气旋,气旋中径向与切向速度之比不恒定会增强气流剪切,产生大量湍流小漩涡,使有序运动能量转化为无序热能,大幅增加能量耗散。
鹦鹉螺贝壳,生长时外套膜按固定比例分泌壳质,使新腔室比前一个按固定比例扩大。这种"比例生长"自然形成对数螺线,既节省材料又增强结构强度,让鹦鹉螺能精准调节浮力。

添加图片注释,不超过 140 字(可选)
宝塔花菜以黄金角(137.5°)螺旋生长,实现最密堆积,使光合结构在有限空间内密度最大,达到植物空间利用率的理论最大值。·

添加图片注释,不超过 140 字(可选)
(滑动以查看全文)
黄金角螺旋排列的最密堆积证明
By qwen AI

添加图片注释,不超过 140 字(可选)

添加图片注释,不超过 140 字(可选)

添加图片注释,不超过 140 字(可选)

添加图片注释,不超过 140 字(可选)

添加图片注释,不超过 140 字(可选)

添加图片注释,不超过 140 字(可选)
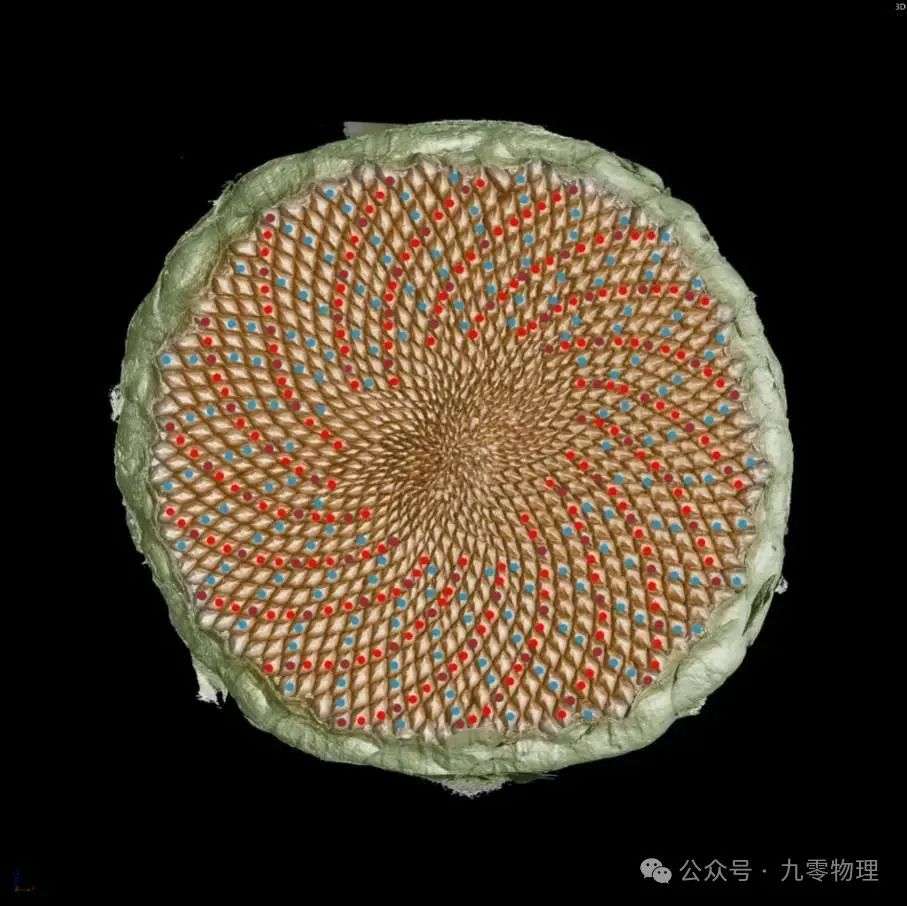
添加图片注释,不超过 140 字(可选)
葵花籽盘多根螺线顺/逆嵌套
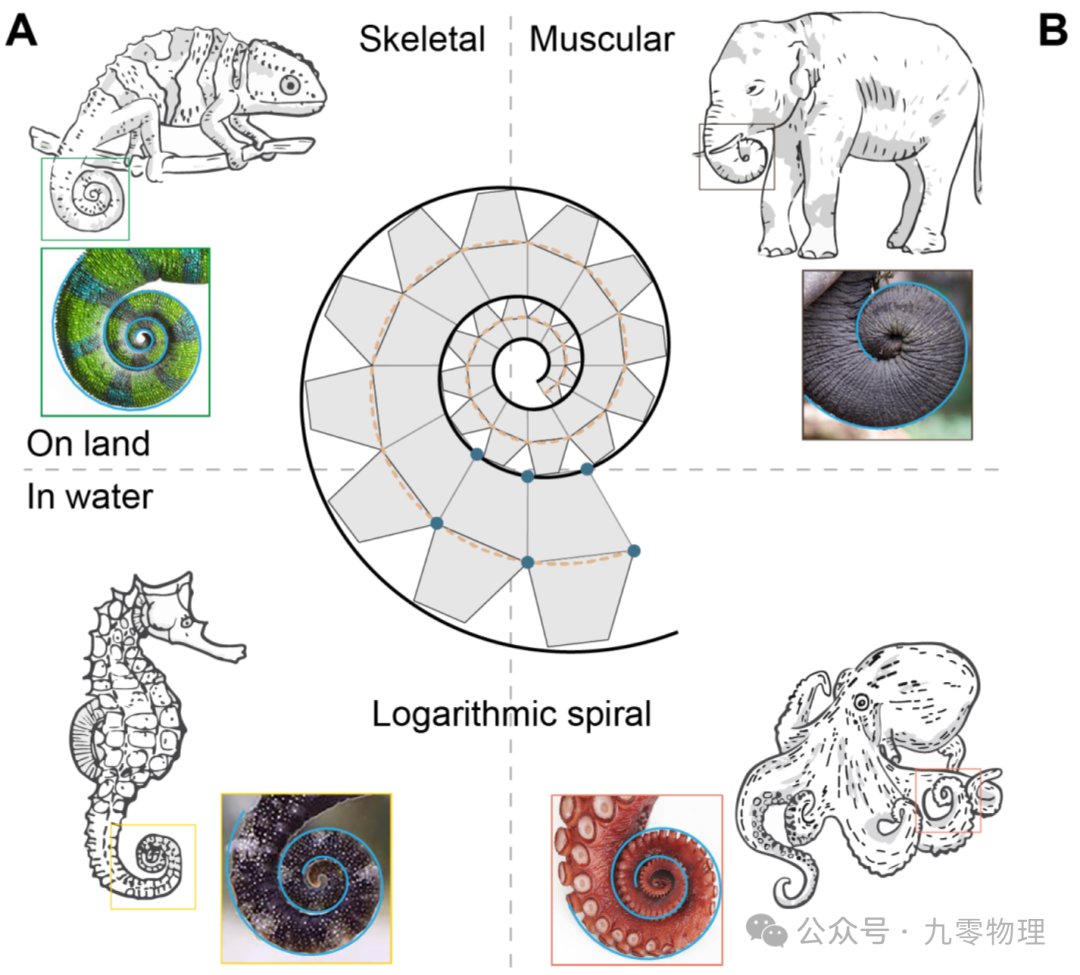
海马尾巴/变色龙尾巴肌肉按黄金角螺旋排列,确保抓握稳定且能耗最低,使应力分布均匀,实现结构强度与能量效率的最佳平衡。
章鱼触手/象鼻,螺旋肌束在无骨骼条件下达到最佳力量输出与精细操作能力。
添加图片注释,不超过 140 字(可选)

添加图片注释,不超过 140 字(可选)
螺旋软体机器人
涡旋星系,引力与旋转平衡形成对数螺线螺旋臂(固定倾斜角12度),结构能量分布均匀,维持星系长期稳定,是宇宙尺度引力系统的自然最优解。

添加图片注释,不超过 140 字(可选)
所以,从微观到宏观,排列、生长、运动……对数螺线主宰的一切,都是大自然按照“结构在一方向的变化速率与另一方向的变化速率之比为定值”的规则而实现能耗、空间、结构的最优设计。
03
数学是大自然的母语吗?
——对数螺线的哲学沉思
大自然用最简洁的数学,创造了最高效的物理结构,这不是偶然——除了对数螺线,还有蜂巢六边形、肥皂泡最小曲面、植物叶序斐波那契数列、河流分叉网络、神经网络……
不禁让我们思考一个古老而深刻的哲学问题:数学是人类发明的描述工具,还是宇宙固有的语言?
柏拉图主义者认为数学对象独立于人类存在,如同"理念世界",而形式主义者则视数学为人类创造的符号游戏。
对数螺线在热带气旋、植物生长、宇宙星辰中的反复出现,似乎支持前者——大自然似乎"懂得"解微分方程dr/dθ = br。
然而更可能的解释是,对数螺线代表了物理系统在能耗最小化、空间最大化约束下的最优解,是简单规则通过演化产生的涌现现象。速度分量比例恒定这一条件,不是自然"遵循"的数学指令,而是物理规律与优化原则的必然结果。
当我们惊叹于自然的数学之美时,或许应该思考:不是数学描述了宇宙,而是宇宙的运作方式塑造了我们对数学的理解。
对数螺线不是自然的"母语",而是我们解读自然的"共同语言"——一种在物理约束下,简单规则产生复杂结构的普遍原理。
这既非纯粹的"发现"也非纯粹的"发明",而是人类认知与自然规律的交汇点。
宇宙或许没有"语言",但它确实有规律,而数学是我们理解这些规律最精确的工具。
微信视频号:sph0RgSyDYV47z6
快手号:4874645212
抖音号:dy0so323fq2w
小红书号:95619019828
B站1:UID:3546863642871878
B站2:UID: 3546955410049087
参考文献链接
人工智能芯片与自动驾驶



 浙公网安备 33010602011771号
浙公网安备 33010602011771号