MLIR中的可组合和模块化代码生成
张量编译器结构的结构化可重定目标方法
7.1.1结构化与可重定目标代码生成流程
用于数值计算的代码生成方法传统上侧重于优化循环嵌套的性能。相关分析侧重于标量元素,因为循环嵌套的主体通常计算单个元素。这样的分析必须考虑内存依赖性与重叠。这些方法在过去进行了深入研究,并已达到高度成熟。当从像C或Fortran这样的输入语言开始时,它们非常适合,其中问题已经根据存储在预分配内存中的数据上的循环来指定。
当关注一个特定的领域(例如ML空间)时,可以在比循环高得多的抽象级别上定义程序。这为重新审视经典的循环优化(如融合、平铺或向量化)提供了机会,而无需复杂的分析与启发式。优点包括降低了复杂性与维护成本,同时还可以自然扩展到稀疏张量等扩展,这些扩展甚至更难在循环级别进行分析。
可以避免在可行的情况下通过静态分析从较低级别的表示中提取信息,并在尽可能高的抽象级别执行优化。将这种方法称为结构化代码生成,因为编译器主要利用源代码中现成的结构信息。如图7-1所示,展示了所涉及的步骤与抽象级别的粗粒度结构。
起点(结构化IR)由张量代数运算组成,作为稠密与稀疏张量上的函数程序组织。
图7-1 结构化与可重构目标代码生成的框架图
从这个级别转换到平铺结构级别,它通过平铺操作引入循环。多个渐进的平铺步骤是可能的,并且不一定会导致标量循环。相反,平铺会在类似于原始操作但在较小张量上的结构化操作环境产生循环。还在这个级别上执行张量运算的融合。选择操作的最终粒度是为了使其硬件映射高效。一个典型的例子是将矩阵乘法平铺以对缓存层次结构进行建模,然后将较小的矩阵乘法直接下译到汇编语言中的超优化微内核。
将生成的小张量的计算映射到(可重定目标的)向量抽象。不需要分析包含精细训练张量运算的控制流。这一步还可能包括启用诸如填充的转换,以实现高效的缓存访问,而不需要缓存行拆分与向量化。
结构化代码生成具有高度可组合性与可重用性,因为平铺与融合转换在操作与数据类型中都是完全通用的。这些转换仅假设与计算与合成数据相关的通用、单调(从集合包含的角度来看)的结构分解模式。密集张量代数与稀疏张量代数都表现出这种分块分解模式,代码生成抽象与基础设施通常适用于这两者。
MLIR中的可组合与模块化代码生成,通用格式的MLIR定义,代码如下:
//第7章/value_definition.c
%value_definition = "dialect.operation"(%value_use) {attribute_name = #attr_kind<"value">} ({
// 区域包含块
^block(%block_argument: !argument_type):
"dialect.further_operation"()[^successor]: () -> ()
^successor:
// 以下更多操作
}): (!operand_type) -> !result_type<"may_be_parameterized">
MLIR具有一组开放的属性、操作与类型。
可以将表示直接转换为MLIR的LLVM方言,以便在CPU上顺序执行,或者卸载GPU内核,或者将循环拆分为异步块,用于并行任务运行时等。
该流程由现有的仿射分析与MLIR中实现的环路优化组成的。
7.1.2 与代码生成相关的方言
设计与实现的特定领域的抽象包括以下方言的表示,这些方言在不断提高的抽象级别中列出。遵循模块化与可选性设计原则,如果这些方言不能为特定情况提供有用的抽象,则可以与其他方言混合,或者直接忽略。
1.向量方言
这种方言提供了固定秩的n-D向量类型,例如向量<4×3×8×f32>,以及形成直观且可重定目标的向量编程模型的操作,该模型在概念上将传统的1-D向量指令扩展到任意秩。这样的操作可以逐渐分解为其自身的较低级别的变体。当后端触发足够健壮以生成接近峰值的集成,或绕过该级别并直接针对硬件特定的内部(例如gpu.subgroup_mma_compute_matrix 2-D向量指令或amx.tile_mulf 2-D网格指令)时,它们进一步下译到LLVM向量指令(例如shufflevector)。
2.GPU方言
GPU方言定义了可重定目标的GPU编程模型。它的特点是SIMT平台通用的抽象,如主机/设备代码分离、工作项/组(线程/块)执行模型、通信与同步原语等。这种方言可以从向量方言中产生,并且可以下译到定制平台的方言,如nvvm、rocdl或spirv,这是总体可重定目标的。
3.memref方言
memref方言引入了memref数据类型,它是MLIR中n-D内存缓存的主要表示,也是基于内存的辅助操作的接口,以及管理缓存分配、重叠(memref视图)与访问的操作。与传统指针不同,memrefs是具有显式布局的多维缓存,允许将索引方案与底层存储解耦:memref<10×10×f32,steps:[1,10]>提供列主访问,同时具有行主存储。memref数据类型还提供了一个与外部C代码互操作的API,以便与库交互非常有用。
4.张量方言
张量方言对抽象的n-D张量类型进行运算,但不能在内存中的表示。在编译过程中,静态尺寸的足够小的张量可以直接放置在(向量)寄存器中,而较大或动态尺寸的张量由于缓存处理而被放入存储器中。张量值是不可变的,并且受到定义的约束。使用SSA语义,对张量的操作通常没有负荷。这允许经典的编译器转换,如视觉优化、常量子表达式与死代码消除,或循环不变代码运动,无缝地应用于张量运算,而不管其潜在的复杂性如何。由于张量值是不可变的,因此无法将其写入。相反,值插入操作会创建替换了值或其子集的新张量。
5.SCF方言
结构化控制流SCF方言提供表示循环与条件的操作(例如,没有提前退出的常规scf.fo与scf.while循环以及scf.if条件构造),并将它们嵌入MLIR的SSA+区域形式中。这是在比控制流图更高的抽象层次上构建的,SCF循环操作可以产生SSA值。
6.linalg方言
linalg方言提供了更高级别的计算原语,可以在张量上与memref容器上操作。
7.稀疏张量方言
稀疏张量方言提供了使稀疏张量类型成为MLIR编译器基础结构中的类型与转换,将高级线性化与低级操作桥接,以节省内存并避免执行冗余工作。
7.1.3 下层方言:生成LLVM IR与二进制
MLIR编译器流的简单可视化描述,如图7-2所示。
图7-2 MLIR编译器流的简单可视化描述:(顶部)仅限LLVM方言,(底部)LLVM与x86向量方言,后者包含特定硬件的内在操作。
图7-2(顶部)总结了工具流程。在转换过程的最后,MLIR生成多个编译路径所共有的低级方言。LLVM方言与LLVM IR非常相似,使用这种方言的MLIR模块,可以在移交给LLVM编译器以生成机器代码前被翻译成LLVM IR。这种方言重用内置的MLIR类型,如整数(i32)或浮点(f32)标量。
MLIR提供了一些低级的特定平台的方言:nvvm、rocdl、x86vector、arm_neon、arm_sve、amx等。这些方言部分镜像了LLVM IR内部函数的相应集合,这些函数本身通常映射到硬件指令。除了使这些指令成为一流的操作外,这些方言还定义了使用MLIR的扩展类型系统与其他功能的高级操作。例如,
arm_neon.2 d. sdot: vector <4 ×4× i8 >, vector <4 ×4× i8 > to vector <4×i32 >
操作自然地表达在MLIR多维向量类型上。在转换为LLVM IR前,它首先被下译到
arm_neon. intr. sdot: vector <16×i8 >, vector <16×i8 > to vector <4×i32 >
其对平铺的1-D向量进行操作以匹配LLVM的规则。
7.1.4 转换
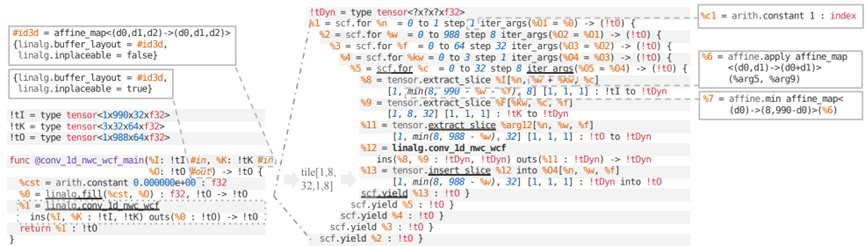
依据linalg.cov_1d_nwc_wcf操作,下译到平铺、填充与向量化形式,在转换IR时逐步规范IR,如图7-3所示。输入IR如图7-3(左)所示。
图7-3 张量上的卷积平铺引入了具有二次推理变量(伪IR)的循环。为了清晰起见,斜体部分被简化,并在标注中扩展。非核心部分指的是新概念:(左)对不可变张量的运算,(右)二次推理变量与张量切片。
这种抽象级对不可变的SSA值进行操作:从现有的张量值创建新的张量值。在随后的下译步骤中,内存位置仅作为函数边界处的注释出现,以指定这些张量将如何具体化到内存中。
对应于linalg.cov_1d_nwc_wcf的索引表示法,由在三维张量上操作的5-D矩形迭代域,用以下表达式给出:
![]()
(7 -1)
在式(7-1)中,迭代域隐含在操作描述中,并且迭代器遍历操作数的整个数据。这是由以下不等式给出的。
![]()
(7-2)
在式(7-2)中,
![]()
表示维数𝑑的第个维度
![]()
。这些量的推导遵循与张量相同的规则。在稠密情况下,可以通过傅立叶-莫兹金方法消去过程导出。
1.平铺
拼接操作引入了scf.for循环,通过子操作(tensor.extract_slice与tensor.insert_slic(5)来访问拼接数据,如图4(右)所示。操作的平铺形式本身就是对平铺子集linalg.cov_1d_nwc_wcf进行操作的。稠密子集的推导是通过每个张量的索引函数计算迭代域的图像获得。
选择了1×8×32×1×8的网格尺寸。虽然这些尺寸是静态的,但有些划分不是整体的,边界网格需要进行完整/部分网格分类。因此,不存在对每个循环迭代有效的单一静态张量类型;平铺张量类型!tDyn必须解耦到一个动态张量。访问网格数据切片的动态大小为%8、%9与%11。
这种张量平铺变换引入scf.for循环执行嵌套,每次迭代时产生全张量的迭代。每个tensor.insert_slice与scf.yield都会产生新值,缓存过程可阻止多余的分配与拷贝。
2.填充值与打包
应用平铺时,内容通常会变得更加动态,以考虑边界效果。这阻碍了需要静态的向量化。有多种缓解方案:
1)平铺可能会引起多级循环剥离(或版本控制),以在主循环中隔离静态的常量部分,然后清除边界循环。
清理循环仍然表现出动态行为,但它们总是可以按1平铺,并进一步减少到大小为1的维度,该维度可以以更细粒度的形式进行向量化。
2)一种替代方案是将动态网格填充到更大的已知静态尺寸。用于填充的值必须是消耗操作的中性值。
3)第三种选择是显式掩模的表示。
为了简洁起见,斜体部分被简化。罗马字体中的常量是属性,斜体是arith.constant运算结果。
即使在没有类型改变,无折叠填充也会在IR中持续存在,并且可以放置在快速缓存器中,尾部类型注释有时为了简洁而省略。当计算不需要足够的时间局部性时,剥离几乎总是更好的选择。一旦某个时间位置可用,填充所需的复制就可以摊销。一旦发生缓存,填充还用于对齐填充缓存中的内存访问。
如图7-4所示,示例中输入张量由3个循环填充提升。这引入了一个特定的网格循环嵌套来预计算填充网格,并将它们插入到类型为包含所有填充网格的压缩tensor<?x?x1x8x8xf32>。在原始网格循环嵌套中,填充被对压缩 tensor%12=tensor.extract_slice%PI的访问所取代。
图7-4 填充平铺操作以获得固定大小的张量(高亮显示),pseudo-IR。
3.向量化
如图7-5所示,在平铺与填充后,卷积操作数是静态成形的,并且处于良好的向量化状态,见图7-5(左)。在当前的IR中,只有两种类型的操作需要向量化:tensor.pad与linalg.cov1d_nwc_wcf。
tensor.pad的向量化是用一个简单的一次性模式实现的,该模式将其简化为一对vector.transfer_read与vector.ttransfer_write操作。有了这样的运算,tensor.pad的向量化相对来说是一个非常小且渐进的下译步骤。
图7-5(右)显示了操作vector.control正在运行。
线性操作向量化遵循向量引入的配置。对于每个操作数transfer_read,以向量形式执行计算,并通过vector.transfer_write将其提交给适当的张量或缓存。vector.transfer操作按照linalg操作的索引表达式进行索引。
每个线性操作都有一个表示计算的标量形式的体区域。体向量化取决于linalg.generic执行的索引类型:
图7-5对固定大小张量的运算可以直接向量化,伪IR。
为了简洁起见,斜体部分被简化,如图7-5所示。向量值是不可变的。它们可以从张量中读取与写入张量。
允许越界访问;读取复制标量操作数,写入被忽略。
1) 在点操作的最简单情况下(索引都是恒等式),每个操作都简单地写成点向量变体;
2) 低维张量操作数可以是向量,将其转换为高维向量;
3) 索引表达式中的置换是用vector.transpose操作处理的;
4) 缩小尺寸低于一级向量,多重缩小取决于对实体的进一步分析;
5) 通过某些维度展开并提取进一步缩减为vector.control或vector.fma的切片,可以特别处理如卷积类的滑动窗口模式。这种简单的策略在捕捉跳跃与增量卷积中提供了高性能。
在图7-5(右)的运行示例中,将展开与%kw循环相对应的尺寸。使用了不会进一步展开的网格尺寸1。注意%16 = vector.extract %15[0] : !vecK运算,这是大小为1的展开切片提取的退化形式。出现了特定的规范化与折叠模式,简化了vector.transfer操作链,并将独立于循环的指令移出循环(例如,. %8 = vector.transfer_read。循环%9 = scf.for与%12 = scf.for,两者都在不插入张量或从张量中提取的情况下产生向量值,这将保证缓存后不会往返内存。所有这些转换都是通过遵循SSA定义实现的。
4.缓存
缓存是将张量值具体化到内存(memref)中的过程。有必要使张量程序通过存储在内存中的数据源具体可执行。在当前的编译管道中,这是最后一步。
MLIR中的张量是不可变的。产生新张量值的运算(可能来自另一个输入张量)在概念上是一个全新的张量。与memrefs不同,这里没有更新/写入张量的概念。为了获得良好的性能,必须遵循以下规则:
1)分配尽可能少的内存;
2)复制尽可能少的内存。
缓存应尽可能重复使用并更新到位,否则当程序转换导致意外分配与复制时,可能会带来巨大的性能损失,如图7-6所示。
图7-6 左侧:输出张量参数,绑定操作结果,采用目标地址传递样式。右边:一个读后写冲突的例子。
写入后读取冲突。为每次内存写入分配一个新的缓存总是安全的,但会浪费内存并引入不必要的复制。另外,如果必须在稍后读取重写的内存位置上的原始数据,则重用缓存并将其写入到位可能会导致无效的缓存化。执行转换时,必须小心地保留依赖关系的程序语义。图7-6的右侧显示了一个潜在的写后读取(RaW)冲突,该冲突阻止了本地缓存。高效缓存与寄存器合并有关,寄存器合并是与消除寄存器到寄存器移动相关的寄存器分配子任务。
目标地址传递风格。目前提供的用于缓存的启发式算法,非常适合目标地址传递方式的操作。在这样的操作中,其中一个张量自变量与生成的张量绑定,用于原位缓存。这样的张量自变量被称为输出张量,见图7-6的左侧。输出张量类似于C++输出参数,这些参数作为非常量引用传递并返回计算结果。除了输出张量(自变量)与运算结果用作缓存约束,对函数语义没有可观察的影响;输出张量看起来仍然是不可变的。在缓存期间,当寻找将运算结果写入的缓存时,只考虑输出张量。
当用scf.fo(下译多维张量运算的自然目标)构成结构化运算时,其原理来源于第一性原理。由于scf.fo产生一个值,因此其嵌套区域必须产生完全定义的张量,而不是任意子集。由于嵌套运算通常应用于张量子集——通常是由线性平铺变换产生的——因此通常会注入一对匹配的extract_slice/insert_slice运算。这些相关的scf.yield操作自然会消耗张量自变量(即,不能有任何后续使用),这使它们成为本地缓存的理想候选者,如图7-7所示所示。
这种启发式设计似乎对在使用linalg方言时处理的IR类型很有效:
1)平铺产生了在平铺子集上迭代的外循环。管理这些子集的操作,如extract_slice、insert_slice,自然是目标地址传递样式。
2)填充、打包、向量化与其他转换,也会在全张量或子集上产生具有目标地址传递语义的操作。
3)linalg.generic本身被设计为目标地址Pass操作。这包括linalg.matmul与任何其他简化为linalg.generic的操作。
图7-7 缓存化将张量值分配给缓存,同时考虑图7-3中的函数级注释#in与#out。数据流被副本所取代,不必要的值在左边被划掉。可以分配临时缓存器以确保连续的访问模式。计算有效载荷方言,如linalg与vector,旨在支持张量与memref(缓存)容器。
可以将tensor.insert作为目标Pass风格的操作示例。运算的张量结果在缓存化框架中可能有一个或多个潜在重叠运算操作数。例如,示例中%0的唯一潜在重叠运算操作数是%A(图7-7,左侧),这意味着缓存化后:
1)buffer(%0) = buffer(%A)
2)或者:buffer(%0)是新分配的缓存。
选择缓存时不考虑其他操作数。对于张量结果没有潜在重叠操作数的运算,总是分配一个新的缓存。例如,tensor.generate总是在缓存后进行分配。
7.1.5向LLVM逐步下译多维向量运算
此时,IR已经达到了由包含多维向量的缓存循环与对这些向量的操作组成的抽象级别。这接近LLVM的C++向量范式,只是对多维向量进行操作,而LLVM只有一维向量。
简单状态下,多维vector.transfer操作低于多个一维vector.load与vector.store操作。当硬件支持时,可以下译到n-D DMA操作。复杂状态下,传输操作下译到广播、传输与屏蔽散射/聚集的组合。在不能确定向量转移在边界内的特定情况下,必须在完全转移与部分转移之间采用特定的分离,类似于网格级别的完全与部分网格分离,如图7-8所示。这在linalg.copy(%21,%22)操作环境的else块中,如图7-8(右)所示。
对n-D向量类型的广泛使用,有效地屏蔽了一种展开与阻塞的向量形式,这种形式在向量硬件上是有效的,不受可能干扰后期向量化的中间编译阶段的影响。在这一点上,这种形式已经准备好逐步下译到一维操作,几乎1-1映射到LLVM IR。
图7-8 向量方言可以逐步下译到对一维向量进行更简单的运算。图示为下译对外部产品的收缩,为简洁起见,斜体部分简化,重复部分省略。较低级别的向量运算需要恒定的索引,并且是通过展开外部维度来生成的。
如图7-9所示,从左侧的向量化矩阵乘积代码开始。该IR(主要)是可重定目标的,因为它使用的是通常与可用硬件指令不对应的更高级别的传输与合同操作。首先应用向量展开,如图7-9(a)所示。这种转换的目标有两个:
1)将向量运算分解为已知的目标很好支持的大小,例如映射到AMX指令;;
2)将2个大小的非幂运算优先处理为2个组合的幂运算,例如,将向量<12×f32>处理为3个向量<4×f32>,以避免次优后端代码生成。所得到的IR仍然是部分可重定目标的,因为转移与契约操作仍然存在,并且需要使用可用方案之一将其下译到更接近硬件的表示。
vector.extract_strided_slice与vector.insert_rided_stice将向量的切片提取并插入到更大的向量中。如果目标形状匹配,折叠图案可能导致插入与提取操作相互抵消。
更高级别的vector.transfer_read通常不能直接下译到加载指令,而是逐步处理:首先,如图7-9(b)所示,使用分步转换;然后,如图7-9 (c)所示,创建1-D加载与广播。根据配置的不同,转置可以通过LLVM的shuffle指令或使用专用的内部函数来实现。
vector.control可以下译到外积、内积或LLVM IR矩阵内部。在图7-9(d)中被下译到外积,以实现到图7-9(e)中SIMD融合的乘加指令的映射。逐步下译的每个阶段都伴随着折叠与视觉优化,这些优化减少了要处理的IR量,并实现了特定的转换。因此,完全下译的向量IR在向量<8×f32>上运行,例如由AVX2支持,并且非常紧凑。示例的结果代码有几十个操作,这些操作已准备好下译到LLVM方言,并进一步转换为LLVM IR。
图7-9 表示矩阵乘积的向量方言运算的渐进式下译:(a)目标形状为2×8×2的向量展开引入了向量切片操作;(b)转移置换被具体化为转置运算;(c)一维传递变为具有形状适应性的平面载荷;(d)收缩重写为外积(其他选项也是可能的),这反过来又下译到(e)融合的乘加指令。
7.2 单线程CPU实验
机器学习内核上评估代码生成框架。所有基准测试都测量单线程CPU性能,并与机器的峰值性能进行比较。
7.2.1引擎实验
MLIR为Python提供了一组绑定,支持通用的IR创建与操作。基础设施旨在促进多级元编程,并推动了这些绑定的设计。还提供了一种嵌入Python中的自定义特定域语言(DSL),称为OpDSL。OpDSL的目的是将API范式从构建编译器IR转变为以简洁、人性化与数学上令人信服的形式表达计算,这在张量理解方面取得了成功。OpDSL中的一种多模态矩阵乘法,代码如下:
//第7章/ linalg_matmul.py
@linalg_structured_op
def matmul(A=tensorDef(T1, S.M, S.K), B=tensorDef(T2, S.K, S.N), C=tensorDef(T3, S.M, S.N, output=True)):
C[D.m, D.n] += cast(T3, A[D.m, D.k]) * cast(T3, B[D.k, D.n])
该流程利用并扩展了用于JIT编译与执行的最小MLIR执行引擎。流处理的结构化数据对象在Python中开放为与Python缓存协议兼容的对象。因此,它们可以转换为NumPy数组,也可以从NumPy阵列转换,后者可以进一步转换为特定框架的数据类型。
此外,在Python中提供了一个测试与基准测试工具,以自动测量编译与运行时以及GFLOP等性能数据,用于计算内存流量。该工具还使用多种转换策略来集成编译与执行,代码如下:
//第7章/Tiling_Expert.py
# 编译专家可以通过将转换类相互链接或与专家链接来定义
SingleTilingExpert = Tile.then(Generalize).then(Vectorize).then(Bufferize).then(LowerVectors).then(LowerToLLVM)
DoubleTilingExpert = Tile.then(SingleTilingExpert)
TripleTilingExpert = Tile.then(DoubleTilingExpert)
# 编译专家可以通过其所包含的转换的选项的融合来参数化
concrete_double_tiling = DoubleTilingExpert(
sizes1=[32, 32], sizes2=[8, 4], pad2=True, vectorize_padding=True, contraction_下译='outer')
7.2.2推进转换
前面描述的转换在Python中作为可配置与可调用的转换对象提供。这些对象可以应用于MLIR模块,并对其执行定制转换。在后台,转换会产生一个自定义的过程管道,由定制转换过程与设置的选项,以及一些正确配置的启用/清理过程组成。然后在模块上运行传递管道。
这里列出了Python中当前可用的转换,见表7-1。某些变换与平铺结合使用。如前所述,多维子集应用于张量、向量、memrefs。最初在经典循环上引入的变换被推广到多维结构化运算,其明确目标是保持结构。转换可能不适用,直到通过平铺将一些循环具体化,作为显式与选择性地丢弃结构的某些部分的一种方式。这反过来又改进了编写模式的转换:匹配条件直到满足先决条件才触发。
例如,交换应用于目标结构化操作进行平铺而产生的循环。同样,剥离只发生在局部网格上。剥离与填充被用作一种手段,以确保主要操作变得固定形状,并且更容易接受向量化。
表7-1 Python中当前可用的转换(及其选项)。某些循环变换仅适用于平铺,并且必须与平铺相结合(例如,剥离或交换)。
|
转换
|
选择
|
|
网格
|
网格尺寸——网格尺寸阵列
interchange——平铺后循环的顺序
pad——是否填充局部网格
pack_paddings—阵列的不可移动填充
hoist_paddings——提升阵列填充的环路数量
peel--剥离部分网格的环
scalarize_dyn_dims—是否为不可向量化(动态)维度释放标量代码
|
|
向量化
|
vectorize_padding——是否对填充操作进行向量化
|
|
PipelineOneParentLoop
|
parent_loop_num —哪个父循环到管道
II —迭代间隔
read_latency —读取操作的延迟
|
|
UnrollOneParentLoop
|
parent_loop_num —-展开哪个父循环
unroll_amount —展开循环的迭代次数
|
|
UnrollOneVectorOp
|
source_shape —-要展平的向量运算的源形态
source_shape —将向量运算展开到的目标形态
|
|
Bufferize
|
无
|
|
Sparsify
|
无
|
|
LowerVectors
|
contraction_lower —如何下译向量收缩(外积/内积,LLVM矩阵内部)
multi_reduction_ lower —如何下译多维约简(内部或外部并行)
transpose_ lower —如何下译转换(元素、平面、向量变换、特定目标)
|
|
LowerToLLVM
|
无
|
表7-1中列出的转换利用附加信息与约束条件,锁定在IR的结构化单元上。例如,对于UnrollOneVectorOp的情况,结构化单元是vector.control,对其当前形状有特定限制,并在转换后提供目标形状。
7.2.3实验设置
实验在3.00GHz的Intel Xeon Gold 6154 CPU上运行。这是一款具有AVX512 fma指令与32KB L1D、32KB L1I、每个内核1MB L2缓存,以及由18个内核共享的统一25MB L3的处理器。单线程单精度计算峰值为192GFLOP/𝑠 (每个周期2次fma运算,16f32上各进行2次运算(mul+ad)。单核的理论L1带宽为384GB/𝑠 (假设每个周期有1个加载与1个存储指令,每个指令64B。在科学计算与LLVM基准测试的特权模式下,测量几乎是赤裸裸的,尤其是禁用turbo boost、地址空间随机化与运行的核心的SMT对。还运行在由单个核组成的特定屏蔽CPU指令集中,并将所有进程从执行的内核迁移出去。
用一个简单的连续拷贝基准进一步测量了峰值内存带宽/𝑠 ,通过微调发现,这个最大值出现在12.8KB的读缓存大小(即25.6KB的总缓存大小,或大约L1容量的80%)。考虑到该峰值带宽分析的大小与变换,在64B边界处进行分配以保证不存在高速缓存线分割。由于硬件每个周期可以发布2个负载与1个存储,还将测量带宽的目标缩放外推到给定场景的实际负载/存储组合(即,通过将峰值带宽机械缩放到使用复制基准测量的峰值带宽的50%)。根据基准,顶线是测量的复制带宽(例如,用于转置或缩减)或外推带宽(例如用于执行1次写入的多次读取的深度卷积)。
所有实验都由在基准系统上测量的单线程执行时间组成。进行了100次测量并绘制了中位数。黑色误差条显示了量化测量方差的25%与75%分位数。报告了由于强制缓存未命中与其他过热而放弃预热迭代后的稳态性能。这种开销与需要融合以保持L1热的大规模实验有关。将基准测试结果与参考实现进行比较,以确保正确性。
7.2.4基准测试
评估了在基础设施中针对一系列内核开发的策略的有效性,这些内核主导了机器学习工作负载的执行时间。所有内核都执行单个张量代数运算。结果突出了原始运算的性能,独立于多个运算中的融合与布局优化机会。
区分内存绑定内核与计算绑定内核。内存绑定内核移动与重新排序数据,以便匹配更密集的计算操作的访问模式。对以下内存绑定内核进行基准测试:
1)拷贝性能是一个重要的性能指标。Copy2D基准测试在存储连续数据的二维张量上运行。与平面一维缓存相比,这种设置使在定向平铺、向量化与展开方面具有更大的灵活性,但在其他方面是等效的。
2)移位是一种普遍存在的操作,有不同的形状与大小。Transpose2D基准实现了二维转置。它是高维转置运算的公约数,因为
![]()
转置可以被重写为在张量内的各个位置处的迭代
![]()
转转置。例如4-D
![]()
置换,可以重写为
![]()
的转置
![]()
。这总是可能的,同时保持输入与输出张量的最快变化维度连续。
3)还原是数据聚合操作,也是一个重要的算法主题。在这里,重点关注与矩阵向量乘积,或数据分析与神经网络中发生的类似操作的带宽限制减少。ColRed2D与RowRed2D基准分别将二维张量的行或列减少为一维张量。
计算绑定内核具有显著的重用性,并且表现出比内存带宽需求高得多的计算能力。因此,它们的执行时间受到计算吞吐量的限制,而不是内存带宽的限制。对以下计算绑定内核进行基准测试:
4)矩阵乘法在数值计算中无处不在。Matmul基准测试实现了纯矩阵乘法。
5)卷积(1-D与2-𝐷的变体)主导了许多机器学习模型的执行时间。专注于所谓的NHWC格式,但使用OpDSL方法生成其他格式是微不足道的。
最后,讨论了深度卷积在与流行的MobileNet模型相关的大小下的性能。Depthwiseconv2D是一个NHWC格式的内核,其计算与通信比具有挑战性。
对于每个基准测试,使用表1的转换手动推导出多达5种专家编译器策略。每种情况都会运行一些手动实验,以设计出良好的寄存器网格大小,从而使L1存储内核的性能较高。然后,固定网格大小,并在每种情况下从5个网格中选择性能最佳的策略。这类似于固定的专家驱动的启发式。系统的自动调谐与搜索空间探索是一个积极研究的领域,有望带来重大改进。
7.2.5内存带宽限制内核的性能
带宽绑定内核可能受到不同级别的内存层次结构的限制,这取决于问题的大小与访问模式。在不同尺度上运行带宽约束内核,并分析它们在所有三个缓存层次结构级别上的性能。在复制基准测试的特定情况下,对不同的2-D向量大小、加载/存储交错与针对每个尺度的循环展开进行小范围搜索。测量的带宽就变成了L1带宽测量值。
1.L1带宽
展示了在尺度适合L1缓存的情况下,所有带宽绑定内核所实现的内存带宽,如图7-10所示。观察到Copy2D内核的最高带宽,每个64B的数据恰好执行1个vector.load与1个vector.load。这个内核不执行任何计算,也不重新排列数据。尽管使用存储在一级缓存中的数据在一个紧密的循环中执行,但基准测试表明,偏移延迟需要足够大的尺度。开始看到200 GB/s区域中的L1带宽性能,仅在4KB左右的读取数据(总共8KB,即25%的L1容量)。200GB/s的L1带宽仅在8KB–14KB的读取数据范围内(总共16KB–28KB,即50-87%的L1容量)保持不变。在大约75%的L1缓存利用率下,最大带宽为289 GB/s。较大的尺度会获得较低的带宽,可能是由于冲突未命中。最后,在L1容量的80%左右,方差开始大幅增加。
图7-10 带宽约束内核的内存带宽尺度适合一级缓存。理论拷贝峰值带宽为384 GB/s(实测为289 GB/s)。转置性能受到xmm负载与ym变换的限制,需要做更多的工作才能获得良好的zmm性能。
Transpose2D在移动时重新排列数据。这会导致比Copy2D的简单1加载1存储模式更复杂的指令序列。实现了Copy2D的30-60%的带宽与高达109 GB/s的L1带宽,以获得最有利的大小。
ColRed2D与RowRed2D读取的数据(完整的二维张量)多于写入的数据(一维张量)。这对测试系统是有益的,该系统每个周期可以执行2次读取与1次写入,见表7-2。同时,执行计算的时间。特别地,RowRed2D沿着向量化维度执行昂贵的水平缩减。虽然ColRed2D实现了高达212 GB/s的高带宽,但RowRed2D的带宽仅高达99 GB/s。较低的性能对于缩减尺寸尤其明显,这是由于英特尔处理器上水平缩减的映射,以及跨越ymm与xmm边界的巨大成本。
表7-2 测量与推理的单核拷贝性能(G(2)/𝑠
|
基准
|
L1 @ 12.8KB
|
L2 @ 20%
|
L2 @ 40%
|
L2 @ 90%
|
L3 @ 40%
|
L3 @ 80%
|
DRAM
|
|
复制(1读+1写/(2)
|
289.5
|
89.3
|
83.9
|
54.8
|
25.7
|
17.2
|
12.2
|
|
外推(2次读取+1次写入/(2)
|
434.25
|
134
|
125.8
|
82.2
|
38.5
|
25.8
|
18.3
|
由此产生的性能并不比Transpose2D与ColRed2D相结合更好。更精细的调谐与更好的AVX-512模式有望在未来改善这种情况。
在数据移动期间重新排列数据或性能计算,会立即减少所实现的L1高速缓存带宽。
2.L2带宽
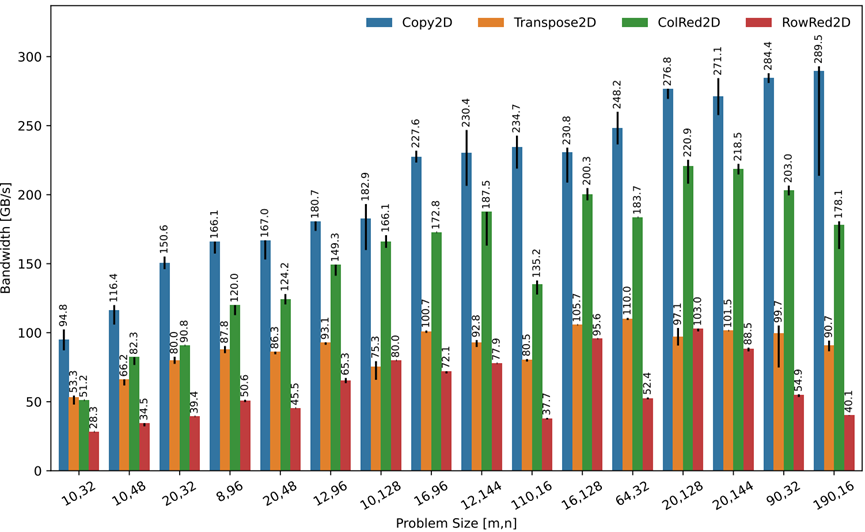
如图7-11所示,展示了适用于二级缓存的大小所实现的内存带宽。ColRed2D与RowRed2D由于其有利的读写效率而实现了最高的带宽,实现了高达125 GB/s的带宽。RowRed2D实现了类似的高带宽,但由于行中最后一个向量的缓慢减少,在向量维度较小的尺度方面也落后了。Copy2D与Transpose2D之间的差异不那么明显,因为重新排列数据的成本与较慢的数据移动部分重叠。
图7-11 带宽约束内核的内存带宽大小适合L2缓存。实测峰值拷贝带宽为83.9GB/𝑠 (每个字节1次读取与1次写入)。约减是一个好办法,因为它们在每次迭代中执行2次读取与一小部分写入。尽管有特定的计算,但放弃大多数写入仍然是一个胜利。
首先,要获得最佳转置版本,英特尔参考优化手册建议使用vblendps指令。向量方言在进入LLVM时,提供了专用的向量传输操作以及多种下译策略。由于使用LLVM IR,因此无法直接控制寄存器分配与指令选择。
为了弥补这种控制不足,特定硬件的向量方言(例如x86向量方言)提供对内部函数的访问,以匹配诸如_mm256_blend_ps之类的clang内部函数。不幸的是,一些clang内部参数(包括_mm256_blend_ps)没有真正的内部实现支持,也不提供对相应ISA的直接访问。相反,它们立即下译到通用LLVM shufflevector指令!LLVM依赖于视觉优化, 尤其是SelectionDAG;但这些包含很少的特定变换组合。在这种情况下,无法编译到所需的vblendps操作。相反,最初不得不接受一个纯粹的基于shuffle的实现。
为了避免这个挑战,还提供了一个InlineAsmOp与特定的基于asm的内部函数,用于对预期指令进行编码(例如,一个mm256BlendPsAsm下译帮助程序,它保证在想要的地址发出vblendps指令)。与LLVM为8×8转置生成的版本相比,这在小转置尺度上提供了30-40%的性能提升,该版本仅使用低于shufflevector的内部函数实现。
3.L3带宽
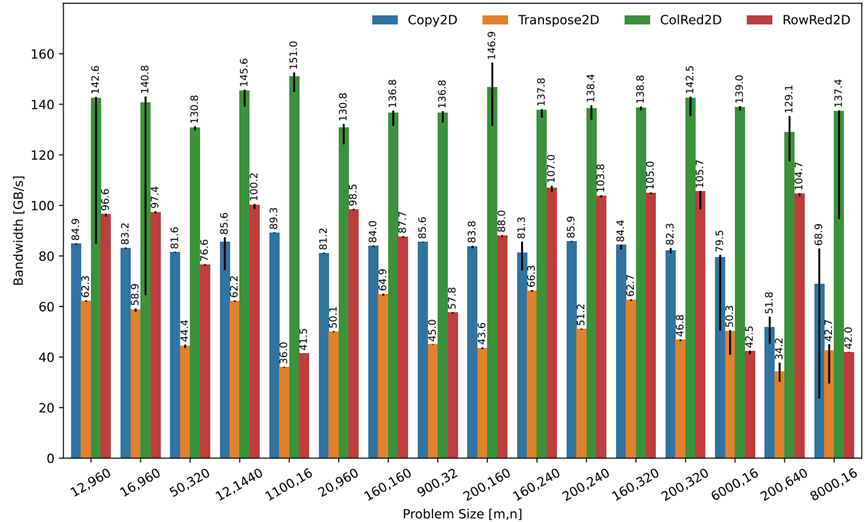
如图7-12所示,展示了适合三级缓存的问题大小所实现的内存带宽。除了Transpose2D外,所有基准测试都在26 GB/s的内存带宽下达到峰值。将这种性能差异归因于L3缓存延迟,该延迟对于转置访问模式来说是无法隐藏的。
图7-12 带宽绑定内核的内存带宽大小适合L3缓存。测量到的拷贝峰值为25.7 GB/s(L3@40%)。250×960×f32的缩减仍然适合L2,因为写入缓存要小得多(即250×f32用于行缩减,960×f32用于列缩减)。
4.转置模式改进
LLVM的视觉优化能够在转置的4×8平铺的非常特殊的情况下恢复模式。虽然没有使用avx512指令,因此可能比希望的慢2倍,但LLVM 4×8版本的性能迄今为止最好。总结了测量数据,见表7-3。
表7-3 载体的中位(p50)测量性能,变换下译策略(GB/s)。自然16×16原生AVX512与移动向量的下译性能,明显不如定制的8×8 AVX2变换vblendps与shufflevector。尽管使用了xmm负载,但4×8平铺与移动向量的性能明显更好。
|
大小
|
Tile8×8Shuffle
|
Tile16×16Shuffle
|
Tile8×8AVX2
|
Tile4×8Shuffle
|
|
16×16
|
24.1
|
22.5
|
41.8
|
55.3
|
|
32×32
|
29
|
27
|
64
|
95
|
基于这一理解,使用UnrollOneVectorOp进行了特定的实验,试图在强制xmm与ymm加载的同时,保持16×16向量的转置大小。此实验导致性能下降,可能是由于尚未规范化的移动向量。需要做更多的工作才能弄清真相。
随着设计出的更适合AVX512版本并更精细地调整网格大小与编解码器策略,性能还有未来改进的空间。预计一个更好的AVX512解决方案,可能会涉及之前的工作。目前,对于完全隔离的2-D转置操作,测量的效率在30%与55%之间,这必须放在附加的上下文中。复制内核为每个操作精确地执行1次64B加载与1次64B存储,但转置核要复杂得多。它们涉及16B与32B负载,但考虑到较小的负载与特定的变换指令,它们仍然达到相对较高的性能。
最后,需要考虑的另一个论点是,转换本身是相互关联的,它们通常与其他操作(例如matmul)组合,在这种情况下,它们的成本通常被摊销。
7.2.6计算约束核的性能
现在回顾一下矩阵乘法与卷积的性能。
1.矩阵乘法
在数值计算中,获得高的矩阵乘法吞吐量是至关重要的。在式(7-1)中,展示了测量纯矩阵乘法与转置变体的性能。
![]()
(7-1)
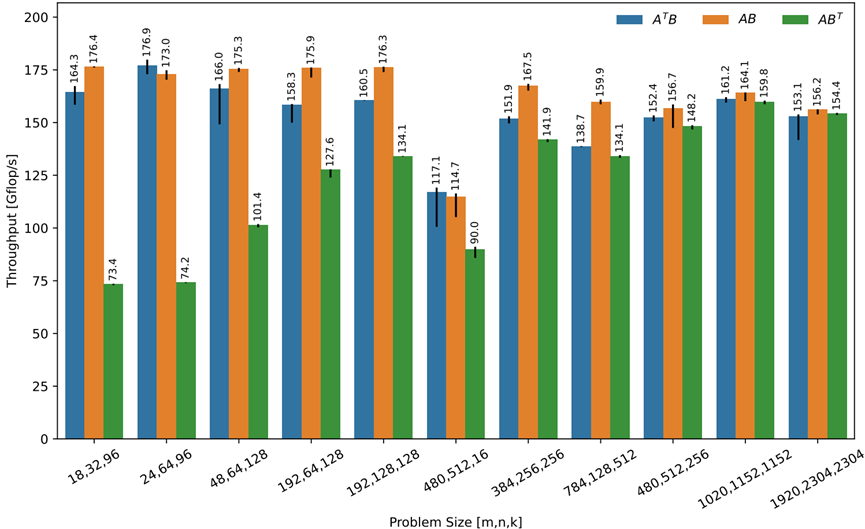
不同大小的矩阵乘法的性能,如图7-13所示。在AB核的情况下,达到了92%的效率,这表明编解码器方法接近峰值的算术强度核。值得注意的是,在低延迟状态的情况下,布局对性能有显著影响。特别是
![]()
由于沿着最快变化的存储器维度的布局(即
![]()
)缩减维度,这是与RowReduction2D类似的水平缩减问题。
图7-13 矩阵乘法计算不同存储布局与大小的吞吐量(5种最佳固定策略),理论峰值为
192GFLOP/𝑠。
在低延迟尺度下,转置的成本令人望而却步,性能也会受到影响。当达到更大的尺度时,转换变得有益,并且没有更多的性能差异。
较大的尺寸使用288×128×512的固定平铺,但没有特别调整。此外,还没有发出预取指令,也没有尝试通过计算来处理数据移动。
2.卷积
卷积将输入张量与遵循滑动窗口模式的多维内核进行折叠,根据卷积算子的输入图像与内核维度来配置卷积算子:
1)𝐻: 图像的高度,
2)𝑊: 图像的宽度,
3)𝑁: 图像的批号(仅输入与输出),
4)𝐶: 图像的输入通道,
5)𝐹: 图像的输出滤波器(仅内核),
其他参数是内核宽度
![]()
与
![]()
, 步长
![]()
与
![]()
, 与扩张
![]()
与。在式(7-2)中,展示了测量NHWC格式的1-D与2-D卷积的性能。
![]()
(7-2)
在这里步长(
![]()
与
![]()
) 与扩张(
![]()
与
![]()
) 参数控制了输入图像访问模式。
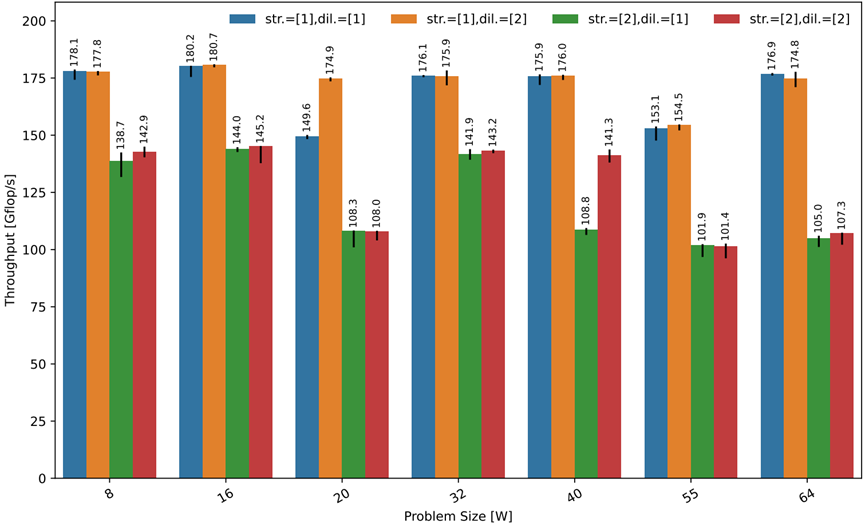
如图7-14所示,展示了一次平铺后1-D(左)与2-D(右)卷积的计算吞吐量。图中未显示的所有问题大小都是恒定的(对于1-D情况,
![]()
对于2-D情况
![]()
)。
图7-14 不同步长、扩张与问题大小的L1存储一维卷积(
![]()
固定到
![]()
),理论峰值为192 GFLOP/s。
当步长为1时,测量了1-D与2-D卷积的高性能,峰值约为理论硬件峰值的96%。观察到非单位步伐放缓。在数据大小非常小并且计算不能弥补访问模式效率的损失的1-D情况下,这种放缓更为明显。低效率在输入大小40以上开始消散,并且在2-D的情况下几乎消失。尺寸20与55不是良好向量大小的完美倍数,并且需要多维循环剥离(把例外的循环直接提取处理),从而导致较低的性能(在这种小的尺寸下填充不是有益的)。
由于这是一个具有多个参数的严格计算约束的内核,只关注向量化内核对于L1中的小尺寸的性能。得益于模块化与可组合方法,可以按照之前讨论的填充、包装与剥离策略,从较小的尺寸构建较大的尺寸。编译器实现了单个一维向量化策略,该策略表现出足够的算术强度,并在二维情况下重复使用。二维策略只需将𝐻与
![]()
维数乘以1,然后将其进一步折叠并规范化。将2-D情况减少到高强度向量化应用模式的1-D情况。


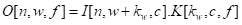
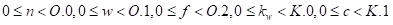
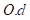






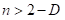
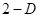

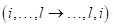

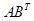
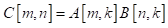
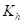
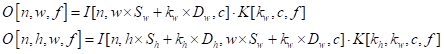

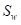
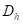
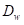
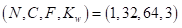
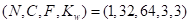
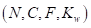
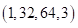
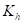



 浙公网安备 33010602011771号
浙公网安备 33010602011771号