一类欧拉函数相关的求和式推导
前言
来源:SGCollin
本文中的题与反演与卷积无关,题目顺序与难度无关。
关于欧拉函数
- 定义:\(\varphi(x)\) 表示 \([1,x]\)里的所有整数中,与\(x\)互质的数的个数
- 欧拉函数的两种常用求法
- 公式法,单点复杂度为\(\sqrt n\),常用于求少量函数值
inline int phi(int x){ int ans=x; for(int i=2;i*i<=x;i++){ if(x%i)continue; ans=ans*(i-1)/i; while(!(x%i))x/=i; } if(x>1){ans=ans*(x-1)/x;} return ans; }- 线性筛,复杂度线性,用于求一个不大的数域内全部的函数值
inline void Euler_phi(int n){ for(int i=2;i<=n;i++)phi[i]=i; for(int i=2;i<=n;i++){ if(phi[i]==i) for(int j=i;j<=n;j+=i) phi[j]=phi[j]*(i-1)/i; } }//好丑...
进入正题
SDOI 2012 Longge的问题
- 题面:求出\(\sum_{i=1}^{n}gcd(i,n)\)
- 数据范围:\(1\le n\le 2^{32}\)
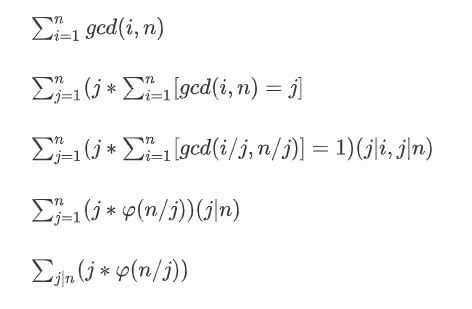
然后就可以切掉这个问题啦
不开ll见祖宗,中间过程变量也是要开ll的(2^32卡int就离谱)
inline ll phi(ll x){
ll ans=x;
for(ll i=2;i*i<=x;i++){//这边记得都要开ll啊
if(x%i)continue;
ans=ans/i*(i-1);
while(x%i==0)x/=i;
}
if(x>1){ans=ans/x*(x-1);}
return ans;
}
inline ll sol(ll x){
ll ans=0,i=1;
for(i=1;i*i<x;i++){
if(x%i==0)ans+=i*phi(x/i)+(x/i)*phi(i);
}
if(i*i==x)ans+=i*phi(i);
return ans;
}
ll n;
int main(){
read(n);
printf("%lld",sol(n));
return 0;
}
SDOI 2008 仪仗队
- 题面:给定一个N*N的方阵,一个人在(1,1),问他最多看到几个人
- 数据范围:\(1\le n \le40000\)
- 问题转化:\(gcd(λx,λy)=λgcd(x,y)>λ⋅1=λ>1\),此时会被遮住。即一个点 (x,y)(x,y) 能被看到,当且仅当\(gcd(x,y)=1\)
- 又因为对角线上只有一个点可以被看到,又因为矩形是对称的所以可以只考虑对角线下面的一半,因此我们求出\(\sum _{i=1}^{n-1}\varphi(i)\),画个图,很容易发现我们漏了一个点,所以最后的答案是\(2*(\sum_{i=1}^{n-1}\varphi(i)+1)+1\)
- 又因为n可能等于1所以要加特判
const int N=40005;
#define int long long
int n,phi[N+105],ans=0;
inline void Euler_phi(int n){
for(int i=2;i<=n;i++)phi[i]=i;
for(int i=2;i<=n;i++){
if(phi[i]==i){
for(int j=i;j<=n;j+=i)
phi[j]=phi[j]/i*(i-1);
}
}
}
signed main(){
scanf("%lld",&n);
if(n==1){
printf("0\n");
return 0;
}
Euler_phi(n-1);
for(int i=1;i<=n-1;i++)ans+=phi[i];
ans=(ans<<1)+3;
printf("%lld",ans);
return 0;
}
GCD
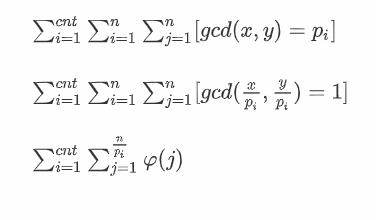
- 题面:给定正整数n,求\(1\le x,y \le n\)且\(gcd(x,y)\)为素数的数对(x,y)有多少对
- 数据范围\(1\le n \le 1e7\)
const int N=10000005;
int cnt,prime[N],phi[N+105];
ll sum[N];
bool is_prime[N];
inline void pre(int n){
memset(is_prime,1,sizeof is_prime);
phi[1]=1;
for(int i=2;i<=n;i++){
if(is_prime[i]){
prime[++cnt]=i;
phi[i]=i-1;
}
for(int j=1;j<=cnt&&1ll*i*prime[j]<=n;j++){
is_prime[i*prime[j]]=0;
if(i%prime[j]){
phi[i*prime[j]]=phi[i]*phi[prime[j]];
}
else {
phi[i*prime[j]]=phi[i]*prime[j];
break;
}
}
}
}
int n;ll ans=0;;
int main(){
scanf("%d",&n);
pre(n+105);
for(int i=1;i<=n;i++)sum[i]=sum[i-1]+phi[i];
for(int i=1;i<=cnt&&prime[i]<=n;i++){
ans+=(sum[n/prime[i]]<<1)-1;//因为i=j时重复了一个
}
printf("%lld",ans);
return 0;
}
写这道题最大的收获是知道了\(phi[1]=1\)
GCD SUM
- 题面:求\(\sum_{i=1}^{n}\sum_{j=1}^{n}gcd(i,j)\)
- 数据范围:\(n\le 1e5\)
- 和上一个题基本一致的思路,只是在累计完个数之后要
*i
const int N=1e5+5;
#define int long long
int phi[N+105];
long long sum[N];
inline void Eluer_phi(int n){
for(int i=1;i<=n;i++)phi[i]=i;
for(int i=2;i<=n;i++){
if(phi[i]==i)
for(int j=i;j<=n;j+=i)
phi[j]=phi[j]*(i-1)/i;
}
}
int n;
signed main(){
scanf("%d",&n);
Eluer_phi(n);
for(int i=1;i<=n;i++)sum[i]=sum[i-1]+phi[i];
long long ans=0;
for(int i=1;i<=n;i++)ans+=(sum[n/i]*2-1)*i;
printf("%lld",ans);
return 0;
}
GCD-Extreme(I)
- 题面:求\(\sum_{i=1}^{n}\sum_{j=i+1}^{n}gcd(i,j)\)
- 数据范围:\(1<n\le 1e5,T<=2e4\)
- 推了半天推不出来,结果看到了某个题解这么写:\(f(n)=gcd(1,n)+gcd(2,n)+gcd(3,n)+……gcd(n-1,n)\)
- 然后可以得到\(G(n)=f(2)+f(3)+……+f(4)\)
- 则,\(G(n)=G(n-1)+f(n)\)
- 由此观之,我们可以通过递推完成这个任务,但重点是如何快速求出\(f(n)=\sum_{i=1}^{n}gcd(i,n)\)
- \(\sum_{i=1}^{n}gcd(i,n)\)然后就可以化简为\(\sum_{i=1}^{n}\varphi(\frac{n}{i})(x|n)\)
const int N=2e5+5;
int phi[N+105];
inline void Euler_phi(int n){
for(int i=1;i<=n;i++)phi[i]=i;
for(int i=2;i<=n;i++){
if(phi[i]==i){
for(int j=i;j<=n;j+=i){
phi[j]=phi[j]/i*(i-1);
}
}
}
}
int n;
long long f[N],sum[N];
int main(){
Euler_phi(200005);
for(int i=1;i<=N;i++){
for(int j=i*2;j<=N;j+=i){//枚举
f[j]+=i*phi[j/i];
}
}
sum[2]=f[2];
for(int i=3;i<=N;i++)sum[i]=sum[i-1]+f[i];
while(1){
n=read();
if(!n)break;
printf("%lld\n",sum[n]);
}
return 0;
}
->对正解来讲是一道题
->双倍经验:SP3871 GCDEX - GCD Extreme
->三倍经验
(spoj前提是你能交上去)
update:2021-07-17 07:41:08 星期六。经一位降维打击的大佬帮助,成功注册了spoj账号可以提交题目了qwq
签到题
- 题面:给出l和r求\(\sum_{i=l}^{r}qiandao(i)\mod 666623333\),其中\(qiandao(x)\)为小于等于x的数中y与x不互质的数的个数
- 数据范围:\(1\le l\le r\le 10^{12},r-l\le 10^6\)
- 很容易发现题目实际上是求\(\sum_{i=l}^{r}i-\varphi(i)\)
- 但是如果直接暴枚的话一定会炸掉,所以我们回到原始计算时的方法(为了让数组移位),先没举\(\sqrt r\)的因数再进行计算就ok啦
#define int long long
long long l,r;
int phi[N+105];
int cnt=0,prime[N+8];
bool vis[N+8];
inline void get_prime(int n){
for(int i=2;i<=n;i++){
if(!vis[i])prime[++cnt]=i;
for(int j=1;j<=cnt;j++){
if(i*prime[j]>n)break;
vis[i*prime[j]]=1;
if(i%prime[j]==0)break;
}
}
}
int c[N];
signed main(){
scanf("%lld%lld",&l,&r);
get_prime(1000000);
for(long long i=l;i<=r;i++){
c[i-l]=i;
phi[i-l]=i;
}
for(int i=1;i<=cnt&&prime[i]*prime[i]<=r;i++){
int pre=prime[i],bgn=l;
if(l%pre){bgn=l/pre*pre+pre;}
for(long long j=bgn;j<=r;j+=pre){
phi[j-l]=phi[j-l]/pre*(pre-1);
while(c[j-l]%pre==0)c[j-l]/=pre;
}
}
long long ans=0;
for(long long i=l;i<=r;i++){
if(c[i-l]>1)phi[i-l]=phi[i-l]/c[i-l]*(c[i-l]-1);
ans=(ans+(i-phi[i-l])%mod)%mod;
}
printf("%lld",ans);
return 0;
}



 浙公网安备 33010602011771号
浙公网安备 33010602011771号