距离 解题报告

距离[2022人大附中特长生T2]解题报告

——by wtz233

题目描述

给出 \(n\) 个点的图，每对不同的点 \((i,j)\) 之间有无向边，地图记录着每对边的距离为\(w_{i,j}\)。任意两点 \(u\) 和 \(v\) 之间（\(u≠v\)）的最短距离记为\(\delta(u,v)\)

形式化地来说，在所有点序列\(a_1,a_2,...,a_k\)中，\(w_{u,a_1}+w_{a_i,a_2}+...+w_{a_k,v}\)的最小值即为\(\delta(u,v)\)，其中 \(k\) 可以是0，此时上式的值就是\(w_{u,v}\)，也就是说\(\delta(u,v) \le w_{u,v}\)

现已知所有的\(\delta(u,v)\)的值，以及\(w_{i,j}\)的最大值刚好等于 \(m\)，但不知道任何\(w_{i,j}\)的值。一张可能的地图，指的是一组合适的\(w_{i,j}\)，满足\(w_{i,j}\)均为非负整数，在此组\(w_{i,j}\)下，所有\(\delta(u,v)\)的值均为给定的值，并且\(w_{i,j}\)的最大值恰好等于m。两张可能的地图被视作不同的，当且仅当至少存在一个\(w_{i,j}\)的值不同。

给定 \(n,m\) 和所有的\(\delta(u,v)\)，请计算一共有多少张可能的地图，并输出结果对\(998244353\)取模的值。注意，如果不存在任何一张地图满足要求，输出0

输入格式

本题单个测试点内有多组数据。首先输入一个整数表示有多少组数据。对于每组数据：

第一行，两个用空格隔开的整数 \(n,m\)

接下来 \(n\) 行，每行 \(n\) 个整数，其中第i行的第j个整数为\(\delta(i,j)\)；保证所有输出的\(\delta(i,i)=0\)，你应当视此为仅仅用于让输入更加美观的占位符，而不需要关心\(\delta(i,i)\)的具体含义。

输出格式

对于每组数据，输出一行一个整数，表示该组测试数据的答案

样例 #1

样例输入 #1

3
3 5
0 3 4
3 0 1
4 1 0
4 5
0 3 1 1
3 0 2 4
1 2 0 2
1 4 2 0
5 6
0 1 0 1 1
1 0 1 0 0
0 1 0 1 1
1 0 1 0 0
1 0 1 0 0

样例输出 #1

1
18
405125

提示

对于所有数据，\(2 \le n \le 400, 0 \le m \le 10^9, 0 \le \delta(i,j) \le 10^9\)，所有 \(n\) 的和不超过800

测试点编号	每个测试点分值	\(n \le\)	\(m \le\)	特殊性质
1	16	4	5	对于\(i ≠ j\)，保证\(\delta(i,j)≠0\)
2	16	40	\(10^9\)	对于\(i ≠ j\)，保证\(\delta(i,j)≠0\)
3,4,5,6	4	400	\(10^9\)	对于\(i ≠ j\)，保证\(\delta(i,j)≠0\)
7	28	400	1	对于\(i ≠ j\)，保证\(\delta(i,j) = 0\)
8	8	40	\(10^9\)
9,10,11,12	4	400	\(10^9\)

题目分析

形式化题意：

给一张完全最短路图，让你求原图最大边权为 \(m\) 的方案数。

正解：

Part 1

我们发现题目中对我们的影响我们解题的要素太多，我们选择先简化问题，我们优先从特殊性质1入手。

我们考虑对于给出的 \({\forall} i ≠ j\)，\(\delta(i,j)≠0\)，那么我们显然可以根据floyd算法得知\(\delta(i,j) = \delta(i,k) + \delta(k,j)(k \neq i,k \neq j)\) 或 \(\delta(i,j) = w(i,j)\) 。那么对于第二情况 \(w(i,j)\) 的取值是唯一的。我们只需考虑第一种情况的取值，很显然只需 \(\delta(i,j) \leq w(i,j) \leq m\) 。如果在不考虑 \(\exists (i,j),w(i,j) = m\) 那么方案数就已经求完了。对于这样一个限制条件，在计数问题中，经典的就是补集转换。我们可以将 \(\exists (i,j),w(i,j) = m\) 转化为 \(w(i,j) \leq m\) 的方案数减去 \(w(i,j) < m\) 的方案数。

为了下面便于形式化的说明，我们将方案数记为 \(ans =\prod A - \prod B\)，其中 \(A\) 为 \(w(i,j) \leq m\) 的方案数，\(B\) 为 \(w(i,j) < m\) 的方案数。

所以

\(A = m - \delta(i,j) + 1 \quad if \quad \delta(i,j) = \delta(i,k) + \delta(k,j)~~(\delta(i,k)\neq 0,\delta(k,j)\neq0)\)

\(B = m - \delta(i,j) \quad\quad ~~~if \quad \delta(i,j) = \delta(i,k) + \delta(k,j)~~(\delta(i,k)\neq 0,\delta(k,j)\neq0)\)

到此我们subtask 1-3已经解决完毕，我们可以获得48pts，相信这在考场上已经是一个不低的分数了。

Part 2

接下来我们考虑0边的影响。

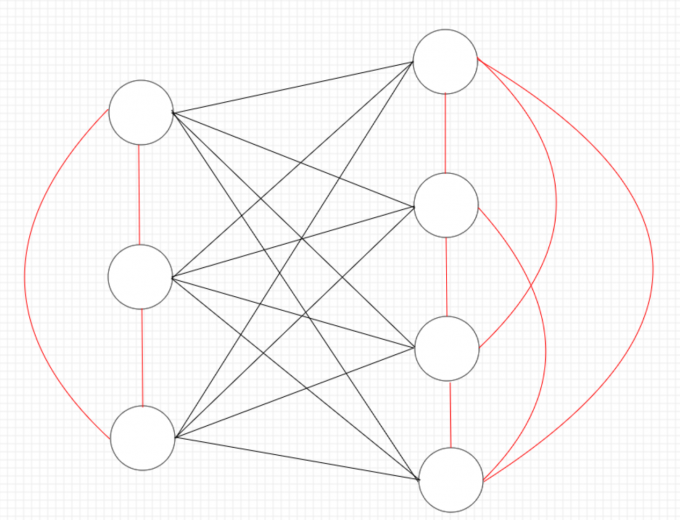
下面为一个示意的图 \(\delta\) 的子图 ，其中红色表示0边，黑色表示非0边。

我们在图 \(w\) 考虑一个点 \(i\) 的所有零边连出来的点构成一个集合，那么该集合的 \(\delta(i,j) = 0\)，即在图\(\delta\) 中构成一个零边完全图。那么图 \(\delta\) 有若干个0边完全图构成，而两两零边完全图间为完全二分图且边权相等，具体可见上图。这里不懂为什么边权相等的可以自己思考一下，读者自证不难。

对于该完全二分图部分的边权，我们考虑到至少要有一个边权为 \(\delta(i,j)\) 。

所以

\(A = (m - \delta(i,j) + 1) ^ {sum} - (m - \delta(i,j))^{sum}\)

$B = (m - \delta(i,j)) ^ {sum} - (m - \delta(i,j) - 1)^{sum} $

其中 \(sum\) 为完全二分图的边数。

Part 3

计算完非零边的贡献，我们接下来考虑零边的贡献。

我们所要计算的是图 \(w\) 最大边权\(\leq m\)，图 \(\delta\) 为零图，图 \(w\) 的方案数。

我们考虑设计dp

\(f(i)\) 表示当前子图点数为 \(i\)，图 $\delta $为零图，最大边权 \(\leq m\)，当前子图的方案数。

直接计算不好计算，那么我们同样考虑补集转化。

\(f(i) = (m + 1)^{\frac{i *(i - 1)}{2}} - \sum_{j = 1}^{j = i - 1}{f(j) * \mathrm{C}_{i - 1}^{j - 1} * m ^{j * (i - j)} * (m + 1) ^ {\frac{(i - j) * (i - j - 1)}{2}}}\);

同理我们也可以设计 \(g(i)\) 来表示当前子图点数为 \(i\)，图 \(\delta\) 为零图，最大边权 \(< m\)，当前子图的方案数。

所以

\(A = f(cnt),~~B = g(cnt)\)，\(cnt\) 为当前零边完全子图的点数。

综上，我们将上述三种情况结合到一起，即可完全解决这个问题。