已知填充(Padding)与步幅(Strides)，如何求输出尺寸？
本文基于李沐老师的《动手学深度学习》（中文版）5.2小节的内容，加了一点个人的理解。
假设输入形状为\(n_h\times n_w\)，卷积核窗口形状为\(k_h\times k_w\)。可以分为以下三种情况讨论，分别是：无填充且步幅为1，有填充且步幅为1，有填充步幅不为1。
1. 无填充且步幅为1时
输出形状将会是
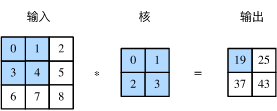
\begin{equation} ( n_h-k_h+1)\times(n_w-k_w+1) \end{equation}如何理解上式呢？（高和宽情况相同，只解释其一即可）。我们将\(n_w-k_w+1\)分为两部分\(n_w-k_w\)和\(1\)，分别用绿色和蓝色标注。绿色部分表示在“宽”这个方向上卷积核可以滑动的次数，当卷积核宽度为\(k_w\)且步幅为1时，滑动的次数刚好等于\(n_w-k_w\)，即图1中白色的列数（等于1，即表示卷积核后续只能滑动1次）。而蓝色部分可以表示该卷积核在开始位置即会输出一个值。红色部分与绿色部分相结合，刚好等于输出的“宽”，即\(n_w-k_w+1\)。
有填充且步幅为1时
按照上述的理解方式，很容易理解有填充时该如何求输出尺寸。如图2所示，假如我们在输入的“宽”方向上填充\(p_w\)列（图2中是左右侧各填充1列），那么绿色部分（即可滑动的次数）应该加上填充的列数，即\(n_w-k_w+p_w\)，而蓝色部分\(1\)不变。则输出尺寸为：
\begin{equation} (n_h-k_h+p_h+1)\times(n_w-k_w+p_w+1) \end{equation}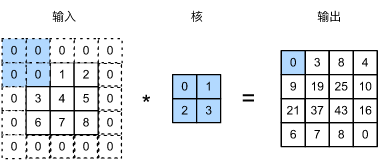
有填充且步幅不为1时
那更进一步，步幅不为1的情况呢？当“宽”上步幅为\(s_w\)时，卷积核可滑动的次数会发生相应的改变，即绿色部分变为：\(\lfloor(n_w-k_w+p_w)/s_w\rfloor\)，该式中的除\(s_w\)和向下取整很容易理解，不多做解释。蓝色部分还是为\(1\)不变，所以输出尺寸为：
\begin{equation} \lfloor(n_h-k_h+p_h+s_h)/s_h\rfloor\times\lfloor(n_w-k_w+p_w+s_w)/s_w\rfloor \end{equation} 当步幅为1时，式(3)即可退化为式(1)和式(2)