20231427田泽航第四周预习报告

1.AI对学习内容的总结

使用AI工具：DEEPSEEK
以下是对其内容的总结：

---

Head First C

第5章：讲解了C语言中的结构体（structs）、联合（unions）与位字段（bitfields）。结构体用于将多个不同类型的数据项组合为单一实体，联合实现在相同内存段中存放不同数据类型，位字段则用于精细调控结构体内各成员所占的位数。这些机制在加密算法实现中常被用于数据结构的封装与内存效率优化，例如定义非对称密钥对或处理原始二进制数据流。

《Windows C/C++加密解密实战》

第6章：讲解RSA算法的基本原理与实现。RSA作为一种非对称加密算法，其安全性建立在大整数分解的数学难题之上。主要内容涵盖素数选取方法、模运算规则、欧拉定理应用，以及公钥与私钥的生成流程和加解密过程。示例代码演示了如何基于小素数完成基础RSA操作，同时指出实际应用中需采用大素数及专门优化算法库以保障系统安全。

第8章：介绍椭圆曲线密码体制（ECC），内容包括椭圆曲线的数学原理、点加与倍点运算规则，以及有限域上ECC的具体实现。相较于RSA，ECC在实现相同安全强度时所需密钥长度更短，特别适用于计算资源受限的场景。

第13章：系统阐述SM2算法的数学基础，包括素域与二元扩域的数学定义、椭圆曲线参数的选取标准与验证方法。SM2作为中国官方推荐的椭圆曲线公钥密码算法，基于ECC框架设计，可广泛应用于数字签名、数据加密与密钥交换等场景。

第14章：重点解析SM2算法的工程实现，涵盖密钥生成、加密解密、数字签名与验证等核心流程，并提供基于MIRACL大数运算库的完整代码示例。本章特别强调了椭圆曲线参数验证与算法实现中的安全注意事项。

教材学习内容总结

2.对AI总结的反思与补充

AI总结的局限性：
1.AI的总结偏向概念层面，未能深入探讨实际编程所涉及的关键细节，例如动态内存的分配与释放、各类异常情况的错误处理机制、以及算法执行效率的优化策略等。

2.对于SM2算法，未详细列出其具体参数与标准曲线（如SM2标准曲线所定义的各项参数值），这可能导致在实际实现过程中难以确保算法的规范性与正确性。

3.在RSA相关内容中，未能充分阐述密钥长度与安全性级别的对应关系，也未强调在实际安全应用中必须使用大素数（例如2048位及以上）来生成密钥，以防范因位数不足导致的破解风险。

自己的补充：

1.结构体和联合的应用：在加密算法实现中，结构体常用于封装密钥数据类型（如分别定义公钥与私钥结构），联合则可用于实现同一内存区域存储多种格式的数据（如整数与字节数组共用内存空间），从而提升代码的灵活性与内存使用效率。

2.RSA实践要点：实际实现RSA算法时，应选用成熟的大整数库（如OpenSSL）处理大数运算，避免因自行实现引入安全风险。密钥生成过程中必须采用安全的随机素数，加密环节则应按照标准使用PKCS#1等填充模式以增强安全性。

3.ECC点运算优化：椭圆曲线密码中的点加与倍点运算涉及模逆与模乘等核心运算，其效率对算法性能至关重要。采用Jacobian坐标进行点表示可有效减少模逆操作次数，显著提升运算速度。

4.SM2实现细节：SM2算法采用特定的椭圆曲线参数（如标准曲线sm2p256v1），所有参数需严格遵循国家密码管理局标准。实现过程中必须验证输入点是否位于曲线上，并正确处理无穷远点情况。其签名机制在ECDSA基础上进行改进，例如采用国密杂凑算法SM3生成消息摘要。

3.学习思维导图

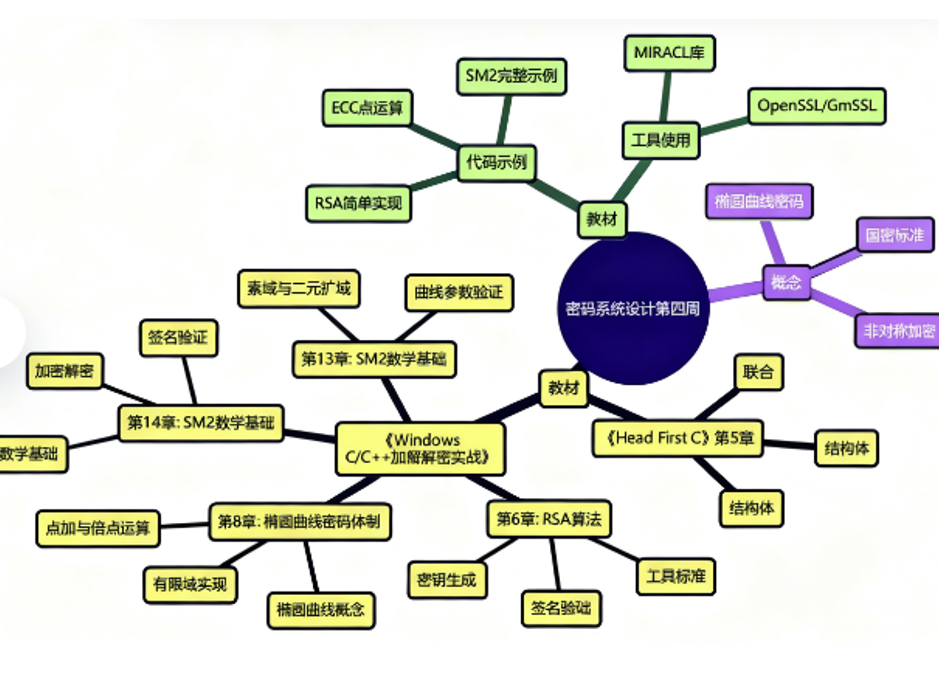
4.基于ai的学习

1. 针对“SM2数字签名算法”
   用户：我正在学习SM2数字签名算法，请你用苏格拉底式方法对我提问，一次一个问题。

AI：SM2数字签名与ECDSA的主要区别体现在哪个环节？

用户：主要体现在哈希算法和签名计算流程上，SM2采用SM3哈希算法并包含用户身份信息。

AI：SM2签名中的Z值是如何生成的？

用户：Z值是通过SM3哈希函数对用户身份、曲线参数和公钥等数据计算得到的预哈希值。

AI：在SM2签名过程中，如何确保随机数k的安全性？

用户：k必须采用密码学安全随机数生成器产生，且每次签名都需更新，否则可能导致私钥泄露。

AI：SM2签名验证时需要执行哪些关键检查？

用户：需要验证签名值(r,s)是否在有效范围内，并重新计算Z值进行签名验证计算。

AI：为什么SM2签名要包含用户身份信息？

用户：这是为了增强身份绑定特性，防止不同用户间签名混淆，提升协议安全性。

AI评价：您已掌握SM2签名的关键流程。

2. 针对RSA加密算法
   用户：我正在研究RSA加密算法的实现，请用苏格拉底方式引导我思考。

AI：RSA算法的安全性建立在什么数学难题之上？

用户：基于大整数分解的困难性，即将两个大质数的乘积分解回原质数在计算上不可行。

AI：在RSA密钥生成过程中，为什么需要选择足够大的素数？

用户：因为使用小素数会导致模数n容易被分解，从而破坏整个密码系统的安全性。

AI：公钥指数e的选择需要满足什么条件？

用户：e必须与φ(n)互质，且通常选择65537以平衡安全性和计算效率。

AI：加密过程中为什么要使用填充方案？

用户：为了防止低指数攻击和确保明文具有一定的随机性，PKCS#1填充还能提供消息格式验证。

AI：如果相同的明文使用相同的公钥加密，会产生什么安全问题？

用户：这会暴露明文信息的模式，攻击者可能通过分析重复的密文破解部分信息。

AI评价：你对RSA的核心概念掌握良好。建议实际调试密钥生成过程，特别注意边界条件和错误处理。推荐结合NIST标准中的密钥长度要求进行实践。

5.学习实践过程遇到的问题与解决方式

问题一：在实现RSA算法时，如何正确生成符合安全要求的大素数？
问题描述
在第6章学习RSA算法实现时，虽然理解了需要采用大素数，但在实际编码中难以有效生成符合密码学安全要求的随机大素数，也不清楚如何验证生成的素数是否合适。

解决方法：

使用成熟密码学库

采用OpenSSL库中的BN_generate_prime_ex()函数，该函数专门用于生成密码学安全的大素数

实现素性检测

结合Miller-Rabin素性测试进行多次检测，确保素数可靠性

设置适当的测试轮数（如64轮）平衡性能与安全性

遵循标准规范

参考NIST FIPS 186-4标准中对素数生成的要求

确保素数长度至少为2048位，且满足特定格式要求（如强素数）

问题二：在实现SM2算法时，如何正确处理椭圆曲线参数验证？
问题描述
学习第13-14章SM2算法时，虽然知道需要验证椭圆曲线参数，但不清楚具体要验证哪些内容，以及如何在实际代码中实现这些验证。

解决方法

严格遵循国密标准

使用GM/T 0003-2012标准规定的sm2p256v1曲线参数

验证曲线方程 是否成立

实现完整的参数验证流程

验证基点G的阶是否为素数n

检查$h = #E(F_p)/n$是否满足安全要求（h≤4）

确保基点G在曲线上且不为无穷远点

使用MIRACL库的验证功能

边界情况处理

特别处理无穷远点的情况

验证签名过程中生成的随机点是否在曲线上

实现输入参数的完整性检查