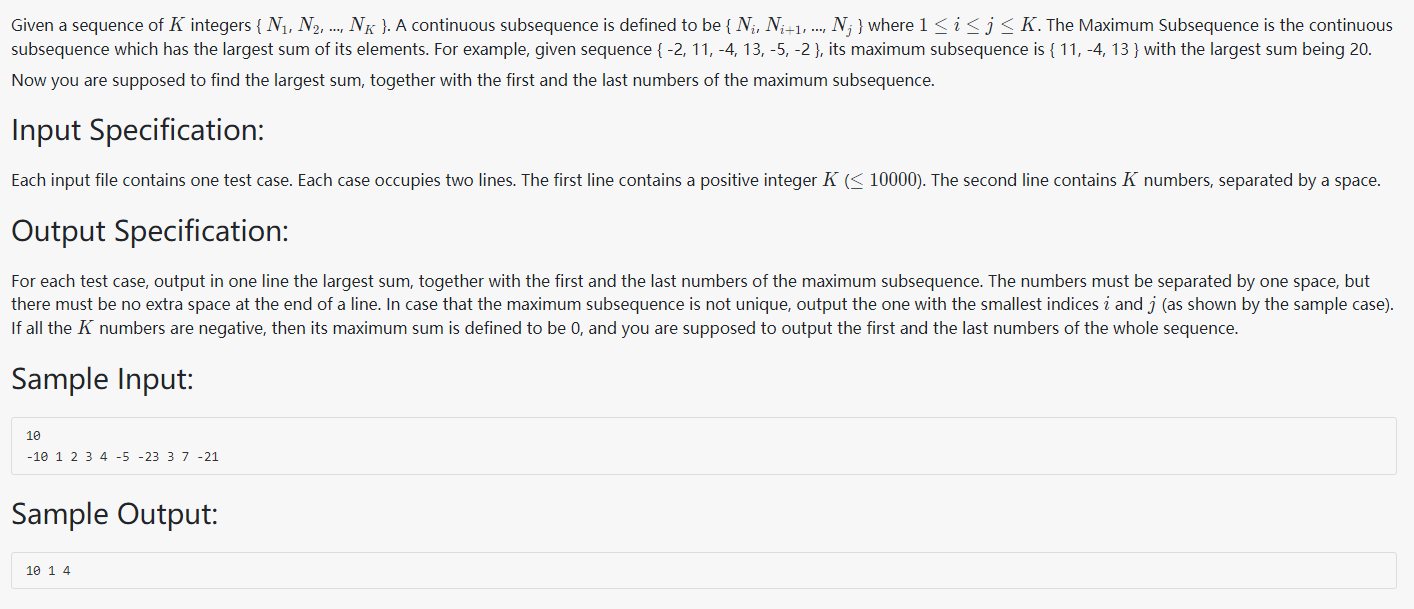
1007 Maximum Subsequence Sum (25分)

这题我说怎么这么熟悉，做过。乙级也有。我感觉这次我写的还是非常简洁的。哈哈。可能是因为做过，所以有一个比较简洁的思路。这题的测试点蛮刁钻（或者说严格），翻看以前的博客，以前发现了几个坑点，但还有东西可以挖掘，稀里糊涂的过了。这次可以详细的记录一下。

何时更新sum？合适更新max？（sum是序列之和，max是所求的最大连续子序列之和）

当sum小于零时，果断令sum=0，抛弃已经为负的序列和，因为任何数加上一个负数只能更小，从新的序列元素开始累加sum；当sum>max时，找到了当前最大的子序列之和，用此刻的sum更新max。

何时更新m,n?(m,n分别记录当前连续子序列有最大和的序列首元素和末元素的秩)

由m,n的定义可知，当max更新时，即可更新这两个变量。同时我在代码中设置了一个m的中间变量tempM,这个中间变量的作用是，每当sum为0之后，记录首个非负元素的秩，这个第一次很难想到为什么要设置这么一个变量，这也是我根据网上找到的测试点，结合我的代码思路来设置的。我出错的测试点有2，4，6.

第四个测试点，输入3 个元素 -1 0 -1时，应输出0 0 0。测试当最大和为0时能否正确输出。

第六个测试点，输入5 个元素1 2 3 0 0时，应输出6 1 3。测试题目给定的要求，“当连续的子序列最大和”不唯一时，输出秩i,j较小的一组。本题就是测试能否正确找到对应的j，即末尾有0，应该抛弃，输出6 1 3而不是6 1 0。

第二个测试点，蛮有意思的，有可能被人忽略的测试点。测试能否正确找到对应的i。其实有两个输入的情况（我之前就是忽略了第二种）：

其一，输入5个元素0 0 0 1 2 3,应输出6 0 3，就是说前面有0，应该保留。（完成这个要求，本测试点可能还不能通过，因为还有一下一种情况）

其二，输入6个元素2 3 -6 0 1 6,应输出7 0 6。我原来的代码输出了7 6 6。插一句话，我是怎么想到这一个奇妙的输入序列呢（没错，是我自己想出来的）。

我解决的方案是，当找到序列最大和max时，才更新m和n。我引入一个变量tempM。它是当sum重新为0时，找到的的一个非负元素的秩（是非负，而不仅仅是正数，因为前面的0要保留）。这是一个新的开始，认定任何新的子序列都有可能是“最大子序列”，用tempM记录这个新序列的首元素的位置，如果之后，这个子序列的和确实比max大，用tempM更新m。如果这个子序列依然没有之前的子序列大，我们也不必担心，因为之前的最大子序列的首元素的位置用m记录，我们没有改变它的值。这是我设置tempM的原因。

下面是代码啦。有人说这题用到了动态规划？不知道，没系统学过。emmm我本来打算好好学一学这种思想的，由于各种原因耽误了，不知不觉中就用了......找时间学一学。

#include<iostream>
using namespace std;
int main(){  
       int K;
       scanf("%d",&K);
       int data[K];
       for(int i=0;i<K;i++)
           scanf("%d",&data[i]);
           
       int sum=0;
       int max=-1,m=0,n=0,tempM=0;
    int label=0;
       for(int i=0;i<K;i++)
       {
           sum=sum+data[i];
           if(label==0)
                {  tempM=i; 
                   label=1;
                }
           if(sum>max)
            {
            max=sum;
            m=tempM;//更新m
            n=i;//更新n 
            }
           if(sum<0)
              {  sum=0;
                 label=0;
              }     
        } 
        
        if(max>=0)
             printf("%d %d %d",max,data[m],data[n]);
        else
        {
            printf("%d %d %d",0,data[0],data[K-1]);
        }
return 0;
}