栈的数学性质：n个不同元素入栈，出栈元素不同排列的个数的推导，卡特兰数（明安图数）的推导
栈的数学性质：n个不同元素入栈，出栈元素不同排列的个数的推导，卡特兰数（明安图数）的推导。
栈的数学性质：n个不同元素入栈，出栈元素不同排列的个数的推导，卡特兰数（明安图数）的推导
前言：重在记录，可能出错。
这部分内容借鉴了网络上的一些内容。如：什么是卡特兰数？和怎么理解出栈顺序有多少种？(递推式的构造)。
一、结论
先说结论，设n个不同元素入栈，出栈元素不同排列的个数为\({f \left( n \right) }\)，则\({f \left( n \right) }\)符合以下规律：
1. $ \color{red}{f \left( n \left) =\frac{{1}}{{n+1}}C\mathop{{}}\nolimits_{{\text{ }2n}}^{{\text{ }\text{ }n}}\right. \right. }$
2. \(\color{red}{f \left( n \left) ={\mathop{ \sum }\limits_{{i=1}}^{{n}}{f \left( i-1 \left) *f \left( n-i \right) \right. \right. }}\right. \right. }\)
3.\(\color{red}{f \left( n+1 \left) =\frac{{4n+2}}{{n+2}}f \left( n \right) \right. \right. }\)
二、推导
1.建立x,y平面直角坐标系。
假设一只小蚂蚁从原点(0,0)出发，将入栈看作向右移动一，出栈看作向上移动一。
当n个不同元素全部入栈、出栈后，有n次入栈和n次出栈，相当于小蚂蚁爬到(n,n)位置。
显而易得的，小蚂蚁共有\(\color{red}{C\text{ }\mathop{{}}\nolimits_{{2n}}^{{n}}}\)种不重复的前进路线（小蚂蚁共需移动2n次，选择其中的n次为向右移动一，则剩下的n次为向上移动一）。
分析，因为栈的特点是只允许在一端进行插入和删除，所以在执行出栈操作时，必须保证栈里存在元素，否则就会抛出栈空异常。即每一步操作，都需要保证此时出栈操作总数≤入栈操作总数。
反映到坐标系上，即小蚂蚁不能越过y=x线或者不能碰到y=x+1线。
显而易得的，对于会抛出异常的输出序列，当其首次抛出异常时，恰好首次出现入栈次数为m，出栈次数为m+1，剩余的入栈次数为n-m，出栈次数为n-m-1，后面的路线有\({C\text{ }\mathop{{}}\nolimits_{{2n-2m-1}}^{{n-m}}}\)种。
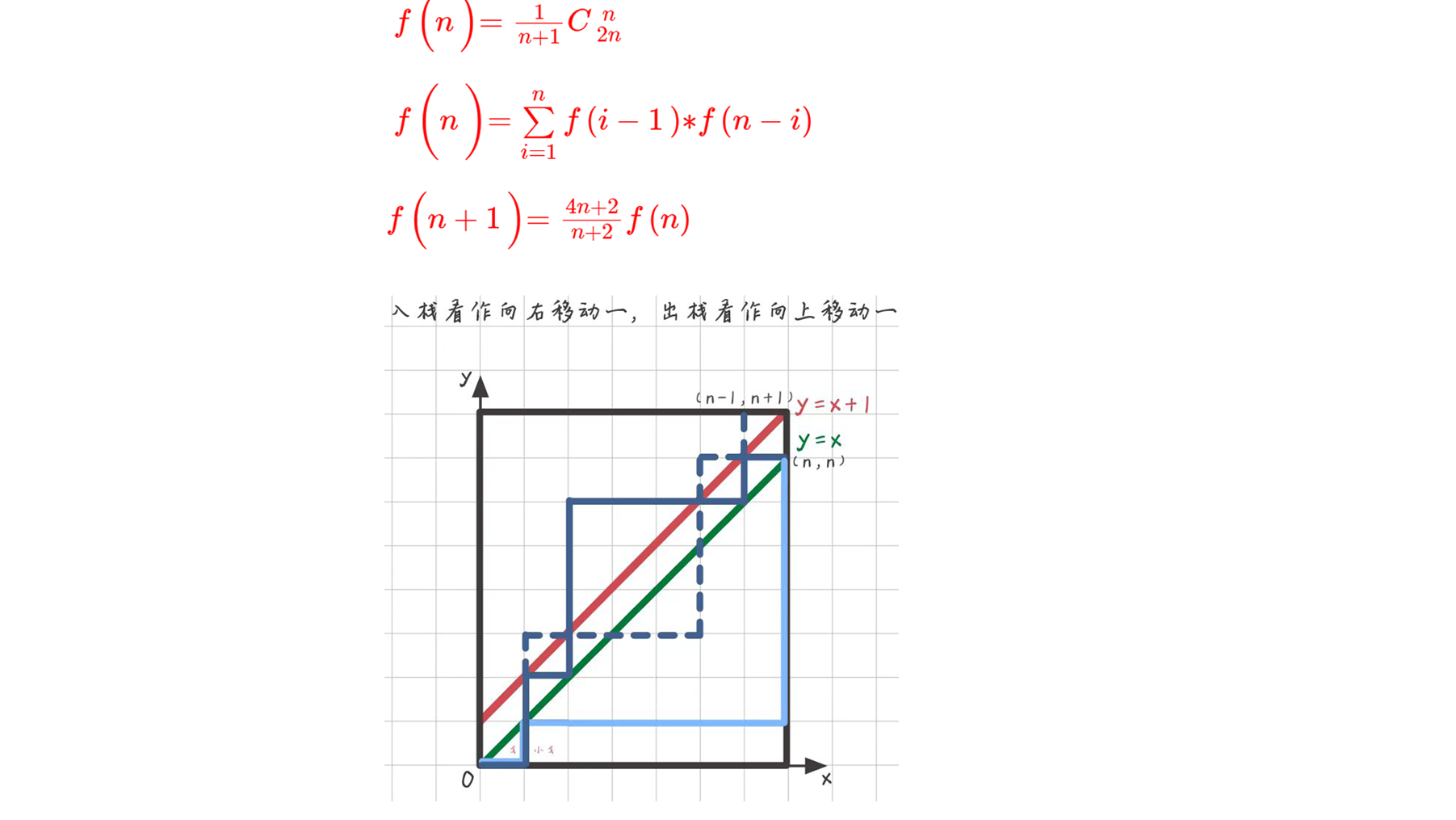
\({C\text{ }\mathop{{}}\nolimits_{{2n-2m-1}}^{{n-m}}}\)，这是在2n-2m-1次操作中，选取n-m次为入栈操作的意思，显而易得的，这个组合数也可以表示在2n-2m-1次操作中，选取n-m次为出栈操作的意思。将n-m次入栈向右移动一，换成n-m出栈向上移动一，反映到坐标系，即将小蚂蚁首次碰到y=x+1后的路线关于y=x+1作对称。如下图：
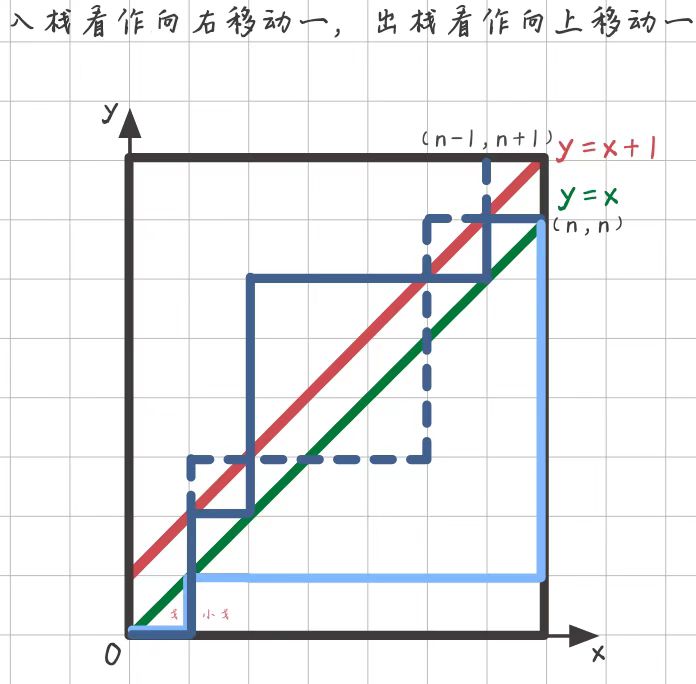
小蚂蚁从(0,0)碰到y=x+1到终点(n,n)就相当于从(0,0)到终点(n-1,n+1)。因此，小蚂蚁所有碰到y=x+1的到(n,n)的路线数就相当于到(n-1,n+1)的路线数，即\(\color{red}{C\text{ }\mathop{{}}\nolimits_{{2n}}^{{n-1}}}\)种。
小蚂蚁从(0,0)到终点(n,n)且不碰到y=x+1的路线有
\[\begin{array}{*{20}{l}}{C\text{ }\mathop{{}}\nolimits_{{2n}}^{{n}}\text{ }-\text{ }C\text{ }\mathop{{}}\nolimits_{{2n}}^{{n-1}}}\\{=\frac{{ \left( 2n \left) !\right. \right. }}{{n!n!}}\text{ }-\text{ }\frac{{ \left( 2n \left) !\right. \right. }}{{ \left( n-1 \left) ! \left( n+1 \left) !\right. \right. \right. \right. }}}\\{=\frac{{ \left( 2n \left) !\right. \right. }}{{n!n!}}\text{ }-\text{ }\frac{{n}}{{n+1}}\frac{{ \left( 2n \left) !\right. \right. }}{{ \left( n \left) ! \left( n \left) !\right. \right. \right. \right. }}}\\{= \left( 1-\frac{{n}}{{n+1}} \left) \frac{{ \left( 2n \left) !\right. \right. }}{{n!n!}}\right. \right. }\\{=\frac{{1}}{{n+1}}C\text{ }\mathop{{}}\nolimits_{{2n}}^{{n}}}\end{array}
\]
综上，设n个不同元素进栈，出栈元素不同排列的个数为\({f \left( n \right) }\)，则\(\color{red}{{f \left( n \right) }=\frac{{1}}{{n+1}}C\text{ }\mathop{{}}\nolimits_{{2n}}^{{n}}}\)。
2.假设n个不同元素为\({a\mathop{{}}\nolimits_{{1}}\text{ }a\mathop{{}}\nolimits_{{2}} \cdots a\mathop{{}}\nolimits_{{n}}}\)，考虑最后一个出栈的元素是谁，是\({a\mathop{{}}\nolimits_{{i}}}\)。
\({a\mathop{{}}\nolimits_{{i}}}\)最后一个出栈，说明\({a\mathop{{}}\nolimits_{{i}}}\)始终在栈底，即当到\({a\mathop{{}}\nolimits_{{i}}}\)的时候，\({a\mathop{{}}\nolimits_{{1}}\text{ }\text{ }a\mathop{{}}\nolimits_{{2}} \cdots a\mathop{{}}\nolimits_{{i-1}}}\)全部完成了正常的入栈、出栈，给\({a\mathop{{}}\nolimits_{{i}}}\)留了一个空栈，这样的序列有\({f \left( i-1 \right) }\)种；
\({a\mathop{{}}\nolimits_{{i}}}\)进入栈底后，不动，此时的栈相当于底厚了一点的“空栈”，等\({a\mathop{{}}\nolimits_{{i+1}}\text{ }\text{ }a\mathop{{}}\nolimits_{{i+2}} \cdots a\mathop{{}}\nolimits_{{n}}}\)全部先完成正常的入栈、出栈，序列有\({f \left( n-i \right) }\)种。总共有\({f \left( i-1 \left) *f \left( n-i \right) \right. \right. }\)种序列。
综上，i的取值为1~n的正整数，所以\(\color{red}{f \left( n \left) ={\mathop{ \sum }\limits_{{i=1}}^{{n}}{f \left( i-1 \left) *f \left( n-i \right) \right. \right. }}\right. \right. }\)
3.我们先算出当n=1,n=2,n=3,n=4,n=5时的\({f \left( n \right) }\)的值，再总结规律，\({f \left( 1 \left) =1,f \left( 2 \left) =2,f \left( 3 \left) =5,f \left( 4 \left) =14,f \left( 5 \left) =42\right. \right. \right. \right. \right. \right. \right. \right. \right. \right. }\)这怎么看规律？就用眼珠子瞪，很简单啊，知道答案，硬凑就行了。!^.^!
\[{\begin{array}{*{20}{l}}{\frac{{f \left( 2 \right) }}{{f \left( 1 \right) }}=\frac{{2}}{{1}},\frac{{f \left( 3 \right) }}{{f \left( 2 \right) }}=\frac{{5}}{{2}},\frac{{f \left( 4 \right) }}{{f \left( 3 \right) }}=\frac{{14}}{{5}},\frac{{f \left( 5 \right) }}{{f \left( 4 \right) }}=\frac{{42}}{{14}}}\\{\frac{{f \left( 2 \right) }}{{f \left( 1 \right) }}=\frac{{6}}{{3}},\frac{{f \left( 3 \right) }}{{f \left( 2 \right) }}=\frac{{10}}{{4}},\frac{{f \left( 4 \right) }}{{f \left( 3 \right) }}=\frac{{14}}{{5}},\frac{{f \left( 5 \right) }}{{f \left( 4 \right) }}=\frac{{18}}{{6}}}\\{\frac{{f \left( n+1 \right) }}{{f \left( n \right) }}=\frac{{6+4 \left( n-1 \right) }}{{n+2}}=\frac{{4n+2}}{{n+2}}}\\{f \left( n+1 \left) =\frac{{4n+2}}{{n+2}}f \left( n \right) \right. \right. }\end{array}}
\]
