线段树分治和平面分治
线段树分治
准确地说应该是按时间轴分治,线段树只是维护分治的工具
通常用于维护答案信息具有可加性(最优子结构),但没有可减性的题目,去掉删除操作
例题0
Luogu P5227 [AHOI2013]连通图
把每次删掉看作先删后加,想到要用并查集维护不能删,所以线段树分治
时间复杂度\(O(nlg^2 n)\)
WA了一次:正着回溯,应该是倒着(应以为戒了)
TLE了一次:size()-1导致0-1变成?
#include<bits/stdc++.h>
using namespace std;
const int N=2e5+5,M=8e5+5;
int n,m,E1[N],E2[N],sz[N],f[N],R[N],lst[N];
struct A{int x,y; };
vector<A>c[M];
void ins(int p,int l,int r,int x,int y,A k) {
if(l==x&&r==y) {
c[p].push_back(k);
return;
}
int mid=l+r>>1;
if(y<=mid) ins(p<<1,l,mid,x,y,k);
else if(x>mid) ins(p<<1|1,mid+1,r,x,y,k);
else {
ins(p<<1,l,mid,x,mid,k);
ins(p<<1|1,mid+1,r,mid+1,y,k);
}
}
inline int find(int x) {
while(x!=f[x]) x=f[x];
return x;
}
void dfs(int p,int l,int r) {
vector<A>tmp,V1,V2;
for(A t:c[p]) {
int u=find(t.x),v=find(t.y);
if(u!=v) {
if(R[u]>R[v]) {
tmp.push_back((A){v,f[v]});
V2.push_back((A){u,sz[u]});
f[v]=u,sz[u]+=sz[v];
} else if(R[u]==R[v]) {
tmp.push_back((A){v,f[v]});
V1.push_back((A){u,R[u]});
V2.push_back((A){u,sz[u]});
f[v]=u,R[u]++,sz[u]+=sz[v];
} else {
tmp.push_back((A){u,f[u]});
V2.push_back((A){v,sz[v]});
f[u]=v,sz[v]+=sz[u];
}
}
}
int u=find(1);
if(sz[u]==n) {
for(int i=l;i<=r;i++) puts("Connected");
if(tmp.size())
for(int i=(int)tmp.size()-1;i>=0;i--) {
f[tmp[i].x]=tmp[i].y;
}
if(V1.size())
for(int i=(int)V1.size()-1;i>=0;i--) {
R[V1[i].x]=V1[i].y;
}
if(V2.size())
for(int i=(int)V2.size()-1;i>=0;i--) {
sz[V2[i].x]=V2[i].y;
}
return;
}
if(l==r) {
puts("Disconnected");
if(tmp.size())
for(int i=(int)tmp.size()-1;i>=0;i--) {
f[tmp[i].x]=tmp[i].y;
}
if(V1.size())
for(int i=(int)V1.size()-1;i>=0;i--) {
R[V1[i].x]=V1[i].y;
}
if(V2.size())
for(int i=(int)V2.size()-1;i>=0;i--) {
sz[V2[i].x]=V2[i].y;
}
return;
}
int mid=l+r>>1;
dfs(p<<1,l,mid),dfs(p<<1|1,mid+1,r);
if(tmp.size())
for(int i=(int)tmp.size()-1;i>=0;i--) {
f[tmp[i].x]=tmp[i].y;
}
if(V1.size())
for(int i=(int)V1.size()-1;i>=0;i--) {
R[V1[i].x]=V1[i].y;
}
if(V2.size())
for(int i=(int)V2.size()-1;i>=0;i--) {
sz[V2[i].x]=V2[i].y;
}
}
int main() {
scanf("%d%d",&n,&m);
for(int i=1;i<=m;i++) {
scanf("%d%d",&E1[i],&E2[i]);
}
int K; scanf("%d",&K);
for(int i=1;i<=K;i++) {
int num; scanf("%d",&num);
for(int j=1;j<=num;j++) {
int t; scanf("%d",&t);
if(lst[t]+1<=i-1) ins(1,1,K,lst[t]+1,i-1,(A){E1[t],E2[t]});//,printf("%d %d %d\n",lst[t]+1,i-1,t);;
lst[t]=i;
}
}
for(int i=1;i<=m;i++) {
if(lst[i]<K) ins(1,1,K,lst[i]+1,K,(A){E1[i],E2[i]});//,printf("%d %d %d\n",lst[i]+1,K,i);
f[i]=i,sz[i]=1,R[i]=1;
}
dfs(1,1,K);
return 0;
}
例题1
也就是维护一个上凸包
凸包具有可加性,无可减性,所以可以线段树分治,每个节点储存凸包
那么将从根到对应点路径上的答案的最大值为该点的答案
如果直接做,需要\(O(nlg^2n)\) 的时间复杂度(凸包上需要二分)
能不能不二分呢?
由于答案查询的顺序没关系,所以可以像斜率优化一样,事先按\(-\frac{a}{b}\)从小到大排序,在凸包上暴力删除队尾,则显然时间复杂度和凸包大小相同,为\(O(nlgn)\)
WA了一次,在插入时忘记了即使点在线段树内无区间也要将其删去
理论上还会T一次:每次用vector存储凸包并且调用了c[p].size(),时间复杂度可能会爆
#include<bits/stdc++.h>
#define ll long long
using namespace std;
inline int rd() {
int ret=0;
char ch=getchar();
while(!isdigit(ch)) ch=getchar();
for(; isdigit(ch); ch=getchar()) ret=(ret<<1)+(ret<<3)+ch-'0';
return ret;
}
const int N=2e5+5,M=8e5+5;
int n,m,cnt,top,b[N];
ll ans[N];
struct Po {
int x,y;
} st[N],a[N];
struct A {
int x,y,id;
} Q[N];
vector<Po>c[M];
void ins(int p,int l,int r,int x,int y,Po k) {
if(l==x&&r==y) {
c[p].push_back(k);
return;
}
int mid=l+r>>1;
if(y<=mid) ins(p<<1,l,mid,x,y,k);
else if(x>mid) ins(p<<1|1,mid+1,r,x,y,k);
else {
ins(p<<1,l,mid,x,mid,k);
ins(p<<1|1,mid+1,r,mid+1,y,k);
}
}
inline bool cmp(Po i,Po j) {
return i.x<j.x||i.x==j.x&&i.y<j.y;
}
void dfs(int p,int l,int r) {
sort(c[p].begin(),c[p].end(),cmp);
top=0;
for(Po i:c[p]) {
while(top>1&&(ll)(i.y-st[top].y)*(st[top].x-st[top-1].x)>(ll)(st[top].y-st[top-1].y)*(i.x-st[top].x)) top--;
st[++top]=i;
}
c[p].clear();
for(int i=1; i<=top; i++) {
c[p].push_back(st[i]);
}
if(l==r) return;
int mid=l+r>>1;
dfs(p<<1,l,mid),dfs(p<<1|1,mid+1,r);
}
inline bool cmpA(A i,A j) {
return -(ll)i.x*j.y<-(ll)j.x*i.y;
}
ll ask(int p,int l,int r,int x,Po k) {
top=c[p].size();
while(top>1&&(ll)(c[p][top-1].y-c[p][top-2].y)*k.y<-(ll)k.x*(c[p][top-1].x-c[p][top-2].x)) {
top--;
c[p].pop_back();
}
ll ret=0;
if(top) ret=(ll)c[p][top-1].x*k.x+(ll)c[p][top-1].y*k.y;
if(l==r) return ret;
int mid=l+r>>1;
if(x<=mid) return max(ret,ask(p<<1,l,mid,x,k));
if(x>mid) return max(ret,ask(p<<1|1,mid+1,r,x,k));
}
int main() {
n=rd();
int m=0;
for(int i=1; i<=n; i++) {
int op=rd();
if(op==1) {
a[++m]=(Po) {rd(),rd()},b[m]=cnt+1;
} else if(op==2) {
int x=rd();
if(b[x]<=cnt) ins(1,1,n,b[x],cnt,a[x]);
b[x]=-1;
} else {
++cnt;
Q[cnt]=(A){rd(),rd(),cnt};
}
}
for(int i=1; i<=m; i++) {
if(b[i]!=-1) {
if(b[i]<=cnt) ins(1,1,n,b[i],cnt,a[i]);
}
}
dfs(1,1,n);
sort(Q+1,Q+cnt+1,cmpA);
for(int i=1; i<=cnt; i++) {
ans[Q[i].id]=ask(1,1,n,Q[i].id,(Po){Q[i].x,Q[i].y});
}
for(int i=1; i<=cnt; i++) {
printf("%lld\n",ans[i]);
}
return 0;
}
例题2
二分图\(<=>\)可以黑白染色
所以可以裂点,将每个点裂出黑色,白色两种状态,
然后类似2-set的思维不过是无向图,用并查集维护
如果一个点能从黑色推到白色说明失败,也就是新加的边的两边同色
由于用的是并查集,所以不能删除,只能按秩合并后回溯,时间复杂度\(O(nlg^2n)\)
RE了一次:忘记裂点,数组开小
WA了一次:在输出Yes时忘记回溯,记得每次return时都要清空
#include<bits/stdc++.h>
using namespace std;
const int N=2e5+5,M=4e5+5;
int n,m,K,f[N],d[N];
struct A{int u,v; };
vector<A>V1[M],V2[M],c[M];
void ins(int p,int l,int r,int x,int y,A k) {
if(l==x&&r==y) {
c[p].push_back(k);
return;
}
int mid=l+r>>1;
if(y<=mid) ins(p<<1,l,mid,x,y,k);
else if(x>mid) ins(p<<1|1,mid+1,r,x,y,k);
else {
ins(p<<1,l,mid,x,mid,k);
ins(p<<1|1,mid+1,r,mid+1,y,k);
}
}
inline int find(int x) {
for(;x!=f[x];x=f[x]);
return x;
}
void dfs(int p,int l,int r) {
for(A i:c[p]) {
int u=find(i.u),v=find(i.v);
if(u==v) {
for(int j=l;j<=r;j++) {
puts("No");
}
for(A j:V1[p]) f[j.u]=j.v;
for(A j:V2[p]) d[j.u]=j.v;
V1[p].clear(),V2[p].clear();
return;
}
u=find(i.u),v=find(i.v+n);
if(u!=v) {
if(d[u]<d[v]) {
V1[p].push_back((A){u,f[u]});
f[u]=v;
} else if(d[u]==d[v]) {
V1[p].push_back((A){u,f[u]});
V2[p].push_back((A){v,d[v]});
f[u]=v,d[v]++;
} else {
V1[p].push_back((A){v,f[v]});
f[v]=u;
}
}
u=find(i.u+n),v=find(i.v);
if(u!=v) {
if(d[u]<d[v]) {
V1[p].push_back((A){u,f[u]});
f[u]=v;
} else if(d[u]==d[v]) {
V1[p].push_back((A){u,f[u]});
V2[p].push_back((A){v,d[v]});
f[u]=v,d[v]=d[u]+1;
} else {
V1[p].push_back((A){v,f[v]});
f[v]=u;
}
}
}
if(l==r) {
puts("Yes");
for(A j:V1[p]) f[j.u]=j.v;
for(A j:V2[p]) d[j.u]=j.v;
V1[p].clear(),V2[p].clear();
return;
}
int mid=l+r>>1;
dfs(p<<1,l,mid),dfs(p<<1|1,mid+1,r);
for(A j:V1[p]) f[j.u]=j.v;
for(A j:V2[p]) d[j.u]=j.v;
V1[p].clear(),V2[p].clear();
}
int main() {
scanf("%d%d%d",&n,&m,&K);
for(int i=1;i<=n+n;i++) f[i]=i,d[i]=1;
for(int i=1;i<=m;i++) {
int u,v,l,r; scanf("%d%d%d%d",&u,&v,&l,&r);
if(l<r) ins(1,1,K,l+1,r,(A){u,v});
}
dfs(1,1,K);
return 0;
}
例题3
xor最大值,想到线性基,由异或的性质发现将所有环加入线性基求最大值即可
而每条边只需要出现在一个环里(异或的性质),所以建一棵树,将所有不在树上的边以环的形式加入
对这些环求线性基
线性基难以删除,所以就不删除,只回溯,用线段树维护,用bitset维护
RE了一次:忘记了可能没有询问,时间线段树内RE
WA了一次:回溯时忘记了可能会有重复的,需要从后往前回溯(也直接复制线性基)时间复杂度是\(O(n\frac{L^2}{w})\)
理论上还需要WA一次:在输出0时可能没有输出
#include<bits/stdc++.h>
using namespace std;
const int N=505,M=1005;
int n,m,q,fro[M];
char s[M],op[20];
namespace BCJ {
int f[N];
inline int find(int x) {
int r=x,u;
while(r!=f[r]) r=f[r];
while(x!=f[x]) {
u=x;x=f[x],f[u]=r;
}
return r;
}
inline void init() {
for(int i=1;i<=n;i++) f[i]=i;
}
}
const int len=1000;
bitset<len>a[N],b[M],tmp;
struct A{int v,w; };
vector<A>V[N];
struct B{int u,v,w; }jia[M];
vector<B>E,c[M<<2];
string u,v;
struct D{
bitset<len>a[len];
void ins() {
for(int i=0;i<len;i++) {
if(tmp[i]) {
if(a[i][i]) tmp^=a[i];
else {
a[i]=tmp;
for(int j=i+1;j<len;j++) {
if(a[i][j]) a[i]^=a[j];
}
for(int j=0;j<i;j++) {
if(a[j][i]) a[j]^=a[i];
}
return;
}
}
}
}
void ask() {
tmp.reset();
bool fl=0;
for(int i=0;i<len;i++) {
if(a[i][i]) tmp^=a[i];
if(tmp[i]) putchar('1'),fl=1;
else {
if(fl) putchar('0');
}
}
if(!fl) putchar('0');
puts("");
}
}Ans;
void dfs(int fa,int u) {
for(A v:V[u]) {
if(v.v!=fa) {
a[v.v]=a[u]^b[v.w];
dfs(u,v.v);
}
}
}
void ins(int p,int l,int r,int x,int y,B k) {
if(l==x&&r==y) {
c[p].push_back(k);
return;
}
int mid=l+r>>1;
if(y<=mid) ins(p<<1,l,mid,x,y,k);
else if(x>mid) ins(p<<1|1,mid+1,r,x,y,k);
else {
ins(p<<1,l,mid,x,mid,k);
ins(p<<1|1,mid+1,r,mid+1,y,k);
}
}
struct C{
int i; bitset<len>s;
};
void dgs(int p,int l,int r) {
D ans=Ans;
for(B i:c[p]) {
tmp=a[i.u]^a[i.v]^b[i.w];
for(int j=0;j<len;j++) {
if(tmp[j]) {
if(Ans.a[j][j]) tmp^=Ans.a[j];
else {
Ans.a[j]=tmp;
for(int k=j+1;k<len;k++) {
if(Ans.a[j][k]) Ans.a[j]^=Ans.a[k];
}
for(int k=0;k<j;k++) {
if(Ans.a[k][j]) {
Ans.a[k]^=Ans.a[j];
}
}
break;
}
}
}
}
if(l==r) {
Ans.ask();
Ans=ans;
return;
}
int mid=l+r>>1;
dgs(p<<1,l,mid),dgs(p<<1|1,mid+1,r);
Ans=ans;
}
int main() {
scanf("%d%d%d",&n,&m,&q);
BCJ::init();
for(int i=1;i<=m;i++) {
int u,v; scanf("%d%d%s",&u,&v,s);
int t=strlen(s);
for(int j=len-t;j<len;j++) {
b[i][j]=s[j-len+t]-'0';
}
if(BCJ::find(u)!=BCJ::find(v)) {
BCJ::f[BCJ::find(u)]=v;
V[u].push_back((A){v,i});
V[v].push_back((A){u,i});
} else {
E.push_back((B){u,v,i});
}
}
dfs(0,1);
for(B i:E) {
tmp=a[i.u]^a[i.v]^b[i.w];
Ans.ins();
}
Ans.ask(); int cnt=0,num=0;
for(int i=1;i<=q;i++) {
scanf("%s",op);
if(op[0]=='A') {
int u,v; scanf("%d%d%s",&u,&v,s);
int t=strlen(s); cnt++,num++;
b[num].reset();
for(int j=len-t;j<len;j++) {
b[num][j]=s[j-len+t]-'0';
}
jia[cnt]=(B){u,v,num},fro[cnt]=i;
} else if(op[1]=='h') {
int u; scanf("%d%s",&u,s);
ins(1,1,q,fro[u],i-1,jia[u]);
int t=strlen(s); fro[u]=i;
num++; jia[u].w=num;
b[num].reset();
for(int j=len-t;j<len;j++) {
b[num][j]=s[j-len+t]-'0';
}
} else {
int u; scanf("%d",&u);
ins(1,1,q,fro[u],i-1,jia[u]); fro[u]=-1;
}
}
for(int i=1;i<=cnt;i++) {
if(fro[i]!=-1) {
ins(1,1,q,fro[i],q,jia[i]);
}
}
if(q) dgs(1,1,q);
return 0;
}
例题4
显然y,z无用,只需要求\(Ans=Min((x-x_i)^2+c_i)\)
斜率优化,维护凸包
将空间和由其分化而得的空间连边,显然某个空间上发生的时间影响且只会影响其自述的空间,所以应用DFS序,不能删除,所以采用线段树分治,线段每次加点(红色表示删除)
WA了一次:删除时没有考虑清楚(没有花上面这张图)
RE了一次:没有想到删除可能并不能加凸包(没有花上面这张图)
TLE了一次:没想到每次算VEctor大小会TLE
#include<bits/stdc++.h>
#define ll long long
const double INF=1e18;
using namespace std;
inline ll rd() {
ll ret=0; char ch=getchar(); bool fh=0;
for(;!isdigit(ch);ch=getchar()) fh=(ch=='-');
for(;isdigit(ch);ch=getchar()) ret=(ret<<1)+(ret<<3)+ch-'0';
return fh?-ret:ret;
}
const int N=5e5+5;
int n,m,top[N<<2],dfn[N],sgn,id[N],fro[N];
bool op[N];
ll ans[N];
struct A{int x; ll y; }a[N],st[N];
struct B{int x,y,id; }Q[N];
vector<A>c[N<<2];
vector<int>V[N];
void ins(int p,int l,int r,int x,int y,A k) {
if(l==x&&r==y) {
c[p].push_back(k);
return;
}
int mid=l+r>>1;
if(y<=mid) ins(p<<1,l,mid,x,y,k);
else if(x>mid) ins(p<<1|1,mid+1,r,x,y,k);
else {
ins(p<<1,l,mid,x,mid,k);
ins(p<<1|1,mid+1,r,mid+1,y,k);
}
}
inline bool cmp(A i,A j) {
return i.x<j.x||i.x==j.x&&i.y>j.y;
}
inline double K(A x,A y) {
return (double)(y.y-x.y)/(y.x-x.x);
}
void dgs(int p,int l,int r) {
sort(c[p].begin(),c[p].end(),cmp);
top[p]=0;
for(A i:c[p]) {
while(top[p]&&st[top[p]].x==i.x) top[p]--;
while(top[p]>1&&K(st[top[p]],i)<=K(st[top[p]-1],st[top[p]])) top[p]--;
st[++top[p]]=i;
}
c[p].clear();
for(int i=1;i<=top[p];i++) c[p].push_back(st[i]);
if(l==r) return;
int mid=l+r>>1;
dgs(p<<1,l,mid),dgs(p<<1|1,mid+1,r);
}
void dfs(int u) {
dfn[u]=++sgn;
if(op[u]==0) fro[id[u]]=dfn[u];
else if(op[u]==1) {
if(fro[id[u]]<dfn[u]) ins(1,1,n,fro[id[u]],dfn[u]-1,a[id[u]]);
}
for(int v:V[u]) {
dfs(v);
}
if(!op[u]&&fro[id[u]]<=sgn) {
ins(1,1,n,fro[id[u]],sgn,a[id[u]]);
}
fro[id[u]]=sgn+1;
}
ll ask(int p,int l,int r,int x,int k) {
ll ret=INF;
while(top[p]>1&&K(c[p][top[p]-2],c[p][top[p]-1])>k) top[p]--;
if(top[p]) ret=c[p][top[p]-1].y-(ll)c[p][top[p]-1].x*k+(ll)k*k;
if(l==r) return ret;
int mid=l+r>>1;
if(x<=mid) return min(ret,ask(p<<1,l,mid,x,k));
return min(ret,ask(p<<1|1,mid+1,r,x,k));
}
inline bool cmpx(B i,B j) {
return i.x>j.x;
}
void write(ll x) {
if(x/10) write(x/10);
putchar(x%10+48);
}
int main() {
n=rd(),m=rd(),a[id[1]].y=rd();
for(int i=2;i<=n;i++) {
op[i]=rd(); int u=rd()+1; id[i]=rd();
if(op[i]==0) {
int x=rd(),y=rd(),z=rd(); ll co=rd();
a[id[i]]=(A){x*2,(ll)x*x+co};
}
V[u].push_back(i);
}
dfs(1);
dgs(1,1,n);
for(int i=1;i<=m;i++) {
Q[i].y=rd()+1,Q[i].x=rd(),Q[i].id=i;
}
sort(Q+1,Q+m+1,cmpx);
for(int i=1;i<=m;i++) {
ans[Q[i].id]=ask(1,1,n,dfn[Q[i].y],Q[i].x);
}
for(int i=1;i<=m;i++) write(ans[i]),puts("");
return 0;
}
例题5
异或和最大——线性基
最大割是需要枚举点集,求恰好有一个端点在这个点集上的边的集合
枚举的是点集,不是边集,所以思考如何把边权挪到点上,很简单,把两端点权异或上边权
所以就变成了求点权的最大值,线性基
#include<bits/stdc++.h>
using namespace std;
const int len=1000,N=505,M=4005;
int n,m,fro[N];
bitset<len>tmp,a[N];
vector<bitset<len> >c[M];
char s[M];
void ins(int p,int l,int r,int x,int y,int k) {
if(x>y) return;
if(l==x&&r==y) {
c[p].push_back(a[k]);
return;
}
int mid=l+r>>1;
if(y<=mid) ins(p<<1,l,mid,x,y,k);
else if(x>mid) ins(p<<1|1,mid+1,r,x,y,k);
else {
ins(p<<1,l,mid,x,mid,k);
ins(p<<1|1,mid+1,r,mid+1,y,k);
}
}
struct D{
bitset<len>a[len];
inline void ask() {
bool fl=0; tmp.reset();
for(int j=0;j<len;j++) {
if(a[j][j]) tmp^=a[j];
if(tmp[j]) putchar('1'),fl=1;
else if(fl) putchar('0');
}
if(!fl) putchar('0');
puts("");
}
}ans;
void dfs(int p,int l,int r) {
D Ans=ans
for(auto v:c[p]) {
for(int i=0;i<len;i++) {
if(v[i]) {
if(ans.a[i][i]) {
v=v^ans.a[i];
} else {
ans.a[i]=v;
for(int j=i+1;j<len;j++) {
if(ans.a[j][j]&&ans.a[i][j]) {
ans.a[i]^=ans.a[j];
}
}
for(int j=0;j<i;j++) {
if(ans.a[j][i]) {
ans.a[j]^=ans.a[i];
}
}
break;
}
}
}
}
if(l==r) {
ans.ask();
ans=Ans;
return;
}
int mid=l+r>>1;
dfs(p<<1,l,mid),dfs(p<<1|1,mid+1,r);
ans=Ans;
}
int main() {
int id; scanf("%d%d%d",&id,&n,&m);
for(int i=1;i<=m;i++) {
int u,v; scanf("%d%d%s",&u,&v,s);
if(u==v) continue;
int t=strlen(s); tmp.reset();
for(int j=len-t;j<len;j++) {
tmp[j]=s[j+t-len]-'0';
}
if(fro[u]) {
ins(1,1,m,fro[u],i-1,u);
}
a[u]=a[u]^tmp;
if(fro[v]) {
ins(1,1,m,fro[v],i-1,v);
}
a[v]=a[v]^tmp;
fro[u]=fro[v]=i;
}
for(int i=1;i<=n;i++) {
if(fro[i]) ins(1,1,m,fro[i],m,i);
}
dfs(1,1,m);
return 0;
}
平面分治
用途
解决最近点问题,等等
例题
忘了说明圆心必须在点上,也就是说这题等价于求最近点距离
可以用KD-tree,但这貌似可以分治
按\(x\)排序,每次将区间按照\(x\)均匀分成两半分别处理,再暴力求出左边和右边之间的最近点距离,显然会TLE
考虑优化,这左边和右边的最小答案为\(Ans\),则左边和右边可能更新答案的点距离中线的距离一定是\(<Ans\),这样稍稍快一点,但在点特别密集的时候还是会TLE
再优化
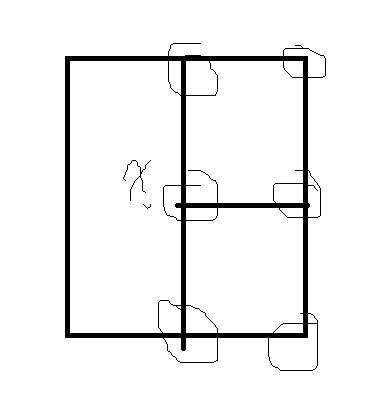
显然对于\(x\)而言的可能更新答案的最近点只能位于右边那两个\(Ans\times Ans\)矩阵,并且一次最多只有6个点(如图),所以每次枚举的最多只有6,所以时间复杂度只有\(O(nlgn)\)
考虑如何枚举:按\(y\)进行单调队列,\(y\)需要有序,采用归并排序
WA了1次,没考虑到归并排序后中线的值会变,需要局部变量
#include<bits/stdc++.h>
#define db double
const int INF=1e9;
using namespace std;
const int N=1e5+5;
int n,q[N];
struct A{db x,y; }a[N],b[N];
inline bool cmp(A i,A j) {
return i.x<j.x;
}
inline db dis(int i,int j) {
return sqrt((a[i].x-a[j].x)*(a[i].x-a[j].x)+(a[i].y-a[j].y)*(a[i].y-a[j].y));
}
db dfs(int l,int r) {
if(l==r) return INF;
int mid=l+r>>1; db d=a[mid].x;
db t1=dfs(l,mid),t2=dfs(mid+1,r),ret=min(t1,t2);
int cnt=0;
int L=1,R=0;
for(int i=l,ta=mid+1;i<=mid;i++) {
if(d-a[i].x<ret) {
while(L<=R&&a[q[L]].y<=a[i].y-ret) L++;
while(ta<=r&&a[ta].y<a[i].y+ret) {
if(a[ta].x-d<ret) q[++R]=ta;
ta++;
}
if(L<=R) {
for(int j=L;j<=R;j++) {
ret=min(ret,dis(q[j],i));
}
}
}
}
int i=l,j=mid+1,k=l;
for(;i<=mid&&j<=r;k++) {
if(a[i].y<a[j].y) b[k]=a[i],i++;
else b[k]=a[j],j++;
}
while(i<=mid) b[k]=a[i],i++,k++;
while(j<=r) b[k]=a[j],j++,k++;
for(i=l;i<=r;i++) a[i]=b[i];
return ret;
}
int main() {
scanf("%d",&n);
while(n) {
for(int i=1;i<=n;i++) {
scanf("%lf%lf",&a[i].x,&a[i].y);
}
sort(a+1,a+n+1,cmp);
printf("%.2lf\n",dfs(1,n)/2);
scanf("%d",&n);
}
return 0;
}
例题2
分治,难点在于求解中间部分
假设两边的答案为\(Ans\),枚举三角形在左边的1个点,则在右边有2个
则右边点(三个点距离加起来\(\leq Ans\))的范围为两个\(\frac{Ans}{2}\times \frac{Ans}{2}\)的正方形(简单几何)
和上题一样,显然这种点不会达到很多,所以暴力,时间复杂度还是\(O(nlgn)\)
#include<bits/stdc++.h>
#define db double
#define ll long long
const int INF=1e9;
using namespace std;
const int N=2e5+5;
int n,q[N];
struct A{int x,y; }a[N],b[N];
inline bool cmp(A i,A j) {
return i.x<j.x;
}
inline db dis(int i,int j) {
return sqrt((ll)(a[i].x-a[j].x)*(a[i].x-a[j].x)+(ll)(a[i].y-a[j].y)*(a[i].y-a[j].y));
}
db dfs(int l,int r) {
if(l==r) return INF;
int mid=l+r>>1,d=a[mid].x;
db t1=dfs(l,mid),t2=dfs(mid+1,r),ret=min(t1,t2);
int L=1,R=0;
for(int i=l,ta=mid+1;i<=mid;i++) {
if(d-a[i].x<ret/2) {
while(L<=R&&a[q[L]].y<=(db)a[i].y-(ret/2)) L++;
while(ta<=r&&a[ta].y<(db)a[i].y+(ret/2)) {
if(a[ta].x-d<ret/2) q[++R]=ta;
ta++;
}
if(L<=R) {
for(int j=L;j<=R;j++) {
for(int k=j+1;k<=R;k++) {
ret=min(ret,dis(q[j],i)+dis(q[j],q[k])+dis(q[k],i));
}
}
}
}
}
L=1,R=0;
for(int i=mid+1,ta=l;i<=r;i++) {
if(a[i].x-d<ret/2) {
while(L<=R&&b[q[L]].y<=(db)a[i].y-(ret/2)) L++;
while(ta<=mid&&a[ta].y<(db)a[i].y+(ret/2)) {
if(d-a[ta].x<ret/2) q[++R]=ta;
ta++;
}
if(L<=R) {
for(int j=L;j<=R;j++) {
for(int k=j+1;k<=R;k++) {
ret=min(ret,dis(q[j],i)+dis(q[j],q[k])+dis(q[k],i));
}
}
}
}
}
int i=l,j=mid+1,k=l;
for(;i<=mid&&j<=r;k++) {
if(a[i].y<a[j].y) b[k]=a[i],i++;
else b[k]=a[j],j++;
}
while(i<=mid) b[k]=a[i],i++,k++;
while(j<=r) b[k]=a[j],j++,k++;
for(i=l;i<=r;i++) a[i]=b[i];
return ret;
}
int main() {
scanf("%d",&n);
for(int i=1;i<=n;i++) {
scanf("%d%d",&a[i].x,&a[i].y);
}
sort(a+1,a+n+1,cmp);
printf("%.6lf\n",dfs(1,n));
return 0;
}

 线段树分治,平面分治,线性基
线段树分治,平面分治,线性基

 浙公网安备 33010602011771号
浙公网安备 33010602011771号