线性代数

线性代数

向量

向量的基本概念

• 向量通常用\(\vec{a}\)或a表示，或使用起始点和终点表示\(\overrightarrow{AB}\) = B - A。

• 向量的长度写作\(\lVert\vec{a}\rVert\)，单位向量表示为\(\hat{a}\) = \(\vec{a}\) / \(\lVert\vec{a}\rVert\)。

• 向量一般用列向量表示：
  $$A = \begin{pmatrix}x\y\end{pmatrix}$$

• 横向量表示为：
  $$A^T = ( x , y )$$

向量的点乘

• \(cos\theta = \dfrac{\vec{a} \cdot \vec{b}}{\lVert\vec{a}\rVert \lVert\vec{b}\rVert}\)

• 向量点乘适用的运算定律：

  交换律 a · b = b · a
  分配律 a · (b + c) = a · b + a · c
  结合律 (ka) · b = a · (kb) = k(a · b)

• 向量的矩阵表示：

  二维向量点乘矩阵表示法：
  
  三维向量点乘矩阵表示法：
  

• 可以根据点乘的结果判断两个向量的接近和远离，还可以判断前后，若两个同向单位向量逐渐远离，则点乘的结果由1变为-1。

向量的叉乘

• 两个向量的叉积（乘）的结果是一个向量，记作c = a x b
  

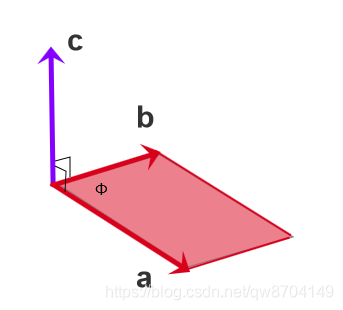
• a x b = -b x a

• \(\lVert\vec{a} * \vec{b}\rVert = \lVert\vec{a}\rVert \lVert\vec{b}\rVert sin\theta\)

• 向量叉乘适用的运算定律:

  分配律 a x (b + c) = a x b + a x c
  结合律 a x (kb) = k(a x b)

• 向量叉乘矩阵表示法:

  向量的叉乘可以写成一个向量对应的矩阵乘以另一个向量
  
  通过矩阵乘法规则推理得出下面结果

• 叉乘可以判断一个向量在另一个的左侧还是右侧

  向量 a 叉乘向量 b > 0, b 向量在 a 向量的左侧
  向量 a 叉乘向量 b < 0, b 向量在 a 向量的右侧

• 还可以判断一个点是否在三角形内部，若边向量分别与三角形顶点和判断点组成的向量叉乘后都判断在同一侧，则点在三角形内。

  

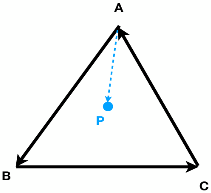
矩阵

矩阵的乘法

A*B的第n行第m列等于A的第n行与B的第m列各个数相乘后相加，如A*B第一行第四列的13等于A第一行的1乘B第四列的4，加上A第一行的3乘B第四列的3。

• 矩阵相乘适用的运算定律

  分配律 A(B + C) = AC + BC
  结合律 (AB)C = A(BC)

  不满足交换律，A*B != B*A。

单位矩阵

一个矩阵的对角线上(从左上角到右下角的对角线）的元素均为1，其余的元素都是0的矩阵称为单位矩阵

• 二维单位矩阵表示为
  
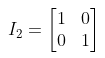
• 三维单位矩阵表示为
  

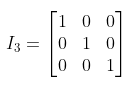
逆矩阵

定义：
若有矩阵 A 和矩阵 B，且 AB = BA = Ⅰ， Ⅰ为单位矩阵，则矩阵A和矩阵B互逆，称矩阵A可逆，矩阵B是矩阵A的逆矩阵

逆矩阵的一些性质：
一个矩阵乘以自身逆矩阵等于单位向量，则它的逆矩阵乘以自己也等于单位向量

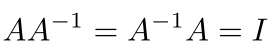
一个矩阵的逆矩阵再作逆运算结果是自己本身

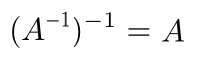
两个矩阵相乘再作逆运算等于后一个矩阵的逆矩阵乘以前一个矩阵的逆矩阵

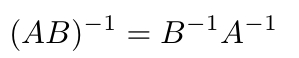
正交矩阵

定义：
若果有矩阵A，满足条件矩阵A乘以矩阵A的转置矩阵是一个单位矩阵，即满足下面的公式

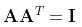
则矩阵A被称为正交矩阵，也就是正交矩阵的逆等于它的转置，可用于旋转矩阵中。

正交阵的一些性质

• 正交矩阵的转置等于它的逆矩阵
• 正交矩阵的每一行都是单位向量，且俩俩正交
• 正交矩阵的每每一列都是单位向量，且俩俩正交