MVP
MVP变换
把三维空间中的物体投影到二维平面上展示,需要经过MVP变换,MVP变换指的是:模型变换(model)、视图变换(view)、投影变换(projection)。模型变换指的是物体的缩放、平移、旋转等变换,视图变换 主要指如何确立相机位置, 投影变换,就是最后最重要的一步,把三维图形投影到二维平面
视图变换(View Transformation)
视图变换又称相机变换,主要学习如何确定一个相机。
确定相机需要三个因素,相机位置、视线方向、上方向
在图形学中相机默认是:相机放在原点,相机方向是-Z方向,上方向是Z轴
假设有一个相机,相机位置是 e,视线方向是 g,上方向是 t,现在需要把它的位置平移到原点位置,视线方向变为-Z,上方向变为Y
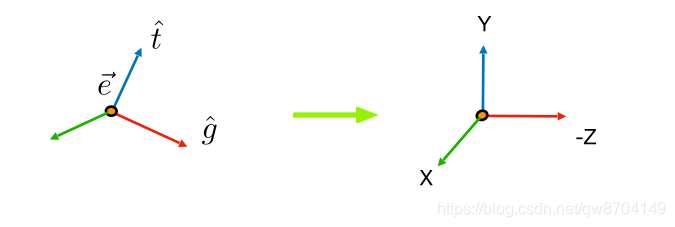
需要怎么做:
- 位置从e平移到坐标原点
- 视线方向从 g 旋转到-Z
- 上方向从 t 旋转到Y,这时g × t 也自动与X重合了
先平移后旋转的矩阵表达式:
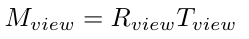
相机位置从e平移到坐标原点的平移矩阵如下:
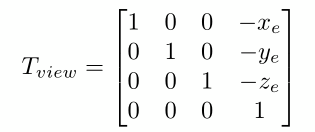
把相机的视线方向 g 旋转到与-Z重合,上方向 t 旋转到与Y重合,g × t 与X重合比较困难,但使用旋转的逆矩阵来表达从标准坐标旋转到相机位置比较简单。视图旋转矩阵的逆矩阵如下:
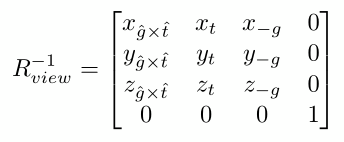
旋转矩阵是正交矩阵,一个正交矩阵的逆矩阵等于它的转置矩阵,那么只要把逆矩阵转置即可得到想要的视图旋转矩阵
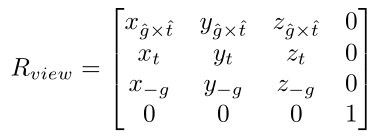
最后得到:
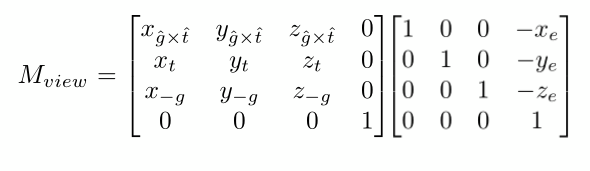
投影变换(Projection Transformation)
正交投影
正交投影会通过远近裁剪面、前后裁剪面、上下裁剪面六个面确定一个可视空间,在可视空间中的物体才能被映射到截面上,
正交投影矩阵推导
假设有一个大小为[l,r]×[b,t]×[f,n]的立方体,希望它的中心移到坐标原点,并把它变换成标准立方体([-1, 1]³), 这个过程需要两种变换,平移变换和缩放变换。
透视投影
透视投影会造成近大远小的效果,也是比较常用的投影方法。
正交投影矩阵推导
可分为两步:
-
先将远截面的四个顶点向内挤压。
可用相似三角形确定挤压比例:
挤压前和挤压后点坐标的矩阵表示:
由此可以推出挤压变换矩阵的部分参数,最后只剩z轴的变换的参数:
由近平面任意一个点在变换后坐标不变可以推出部分参数:
根据矩阵乘法反推,透视投影到正交投影的变换矩阵的第三行的第一列和第二列只能等于0,剩下的第三列和第四列命名为A和B
由此得到:
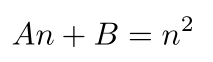
根据远截面上z值不发生变化得到,图中的矩阵表示远截面的中点,f表示中点的z值:
最后由两条式子可推出A和B:
从而完整得出视投影到正交投影的变换矩阵:
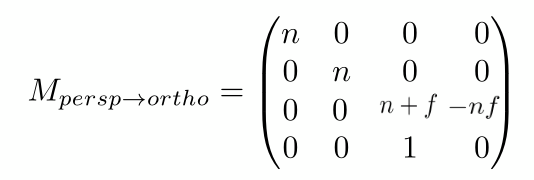
-
后将远截面正交投影到近平面上,也就是再进行一次正交投影。
完整的透视投影矩阵:
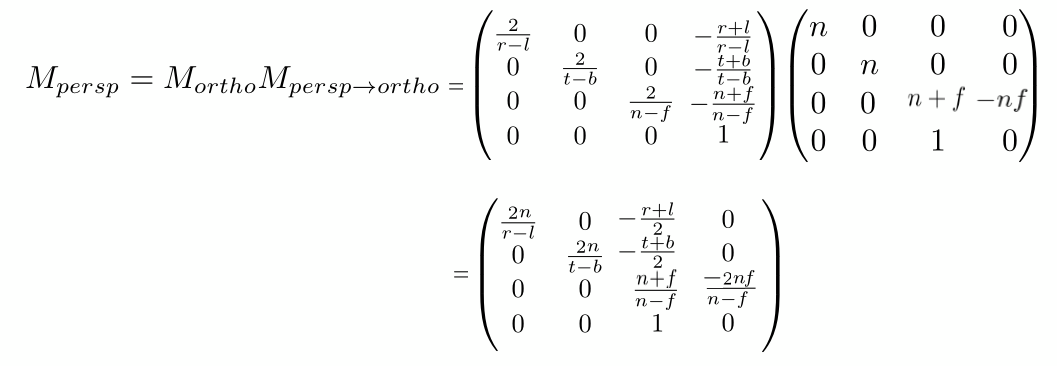



 浙公网安备 33010602011771号
浙公网安备 33010602011771号