向量
单位向量
a = (x, y, z)
len = math.sqrt(x2 + y2 + z2)
normalized = (x/len, y/len, z/len);
![]()
向量点乘
点乘的几何意义是可以用来表征或计算两个向量之间的夹角,以及在b向量在a向量方向上的投影,公式:
具体对应关系为:
a·b>0 方向基本相同,夹角在0°到90°之间
a·b=0 正交,相互垂直
a·b<0 方向基本相反,夹角在90°到180°之间
向量叉积(cross product)
- 向量积,也被称为叉积(即交叉乘积)、外积,是一种在向量空间中向量的二元运算。与点积不同,它的运算结果是一个伪向量而不是一个标量。并且两个向量的叉积与这两个向量都垂直。
- 向量叉积的坐标系表示
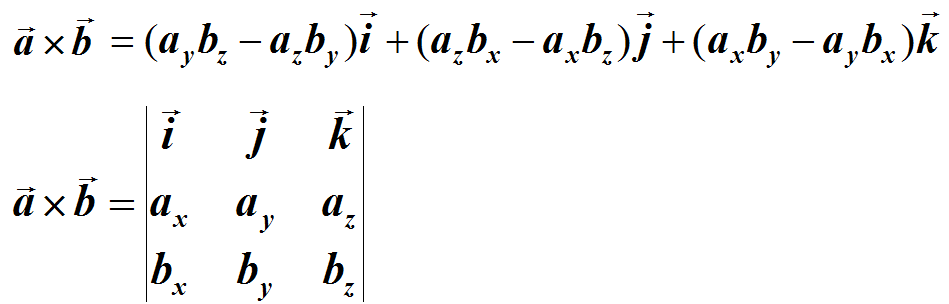
- 右手定则
若坐标系是满足右手定则的,当右手的四指从a以不超过180度的转角转向b时,竖起的大拇指指向是c的方向。由于向量的叉积由坐标系确定,所以其结果被称为伪向量。(unity3d中坐标系满足左手定则,所以使用左手判断)
- 公式
|c| = |a×b| = |a| |b|sin<a,b>


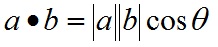

 浙公网安备 33010602011771号
浙公网安备 33010602011771号