TXNLP 09-17

上节课讲了一些算法的复杂度,都比较简单,我就没有单独截图。1 n n^2 nlogn logn。。。等等
其实一些排序问题也比较简单。还是给大家列举一下.
归并排序:

主定理定理。。吐血


算法复杂度相关的知识:函数渐进阶,记号 O、Ω、θ和 o;Master 定理。
先插一句,在算法复杂度分析中,log 通常表示以 2 为底的对数。
算法复杂度(算法复杂性)是用来衡量算法运行所需要的计算机资源(时间、空间)的量。通常我们利用渐进性态来描述算法的复杂度。

比如 T(n) = 2 * n ^ 2 + n log n + 3,那么显然它的渐进性态是 2 * n ^ 2,因为当 n→∞ 时,后两项的增长速度要慢的多,可以忽略掉。引入渐进性态是为了简化算法复杂度的表达式,只考虑其中的主要因素。当比较两个算法复杂度的时候,如果他们的渐进复杂度的阶不相同,那只需要比较彼此的阶(忽略常数系数)就可以了。
总之,分析算法复杂度的时候,并不用严格演算出一个具体的公式,而是只需要分析当问题规模充分大的时候,复杂度在渐进意义下的阶。记号 O、Ω、θ和 o 可以帮助我们了解函数渐进阶的大小。
假设有两个函数 f(n) 和 g(n),都是定义在正整数集上的正函数。上述四个记号的含义分别是:

可见,记号 O 给出了函数 f(n) 在渐进意义下的上界(但不一定是最小的),相反,记号Ω给出的是下界(不一定是最大的)。如果上界与下界相同,表示 f(n) 和 g(n) 在渐进意义下是同阶的(θ),亦即复杂度一样。
列举一些常见的函数之间的渐进阶的关系:

Fibonanci number (斐波那契数)
序列一次为 1,1,2,3,5,8,13,21,.... 问题: 怎么求出序列中第N个数?
T(n) = T(n-2) + T(n-1)
def fib(n):
# base case
if n < 3:
return 1
return fib(n-2)+fib(n-1)
print (fib(50))
斐波那契的时间复杂度:
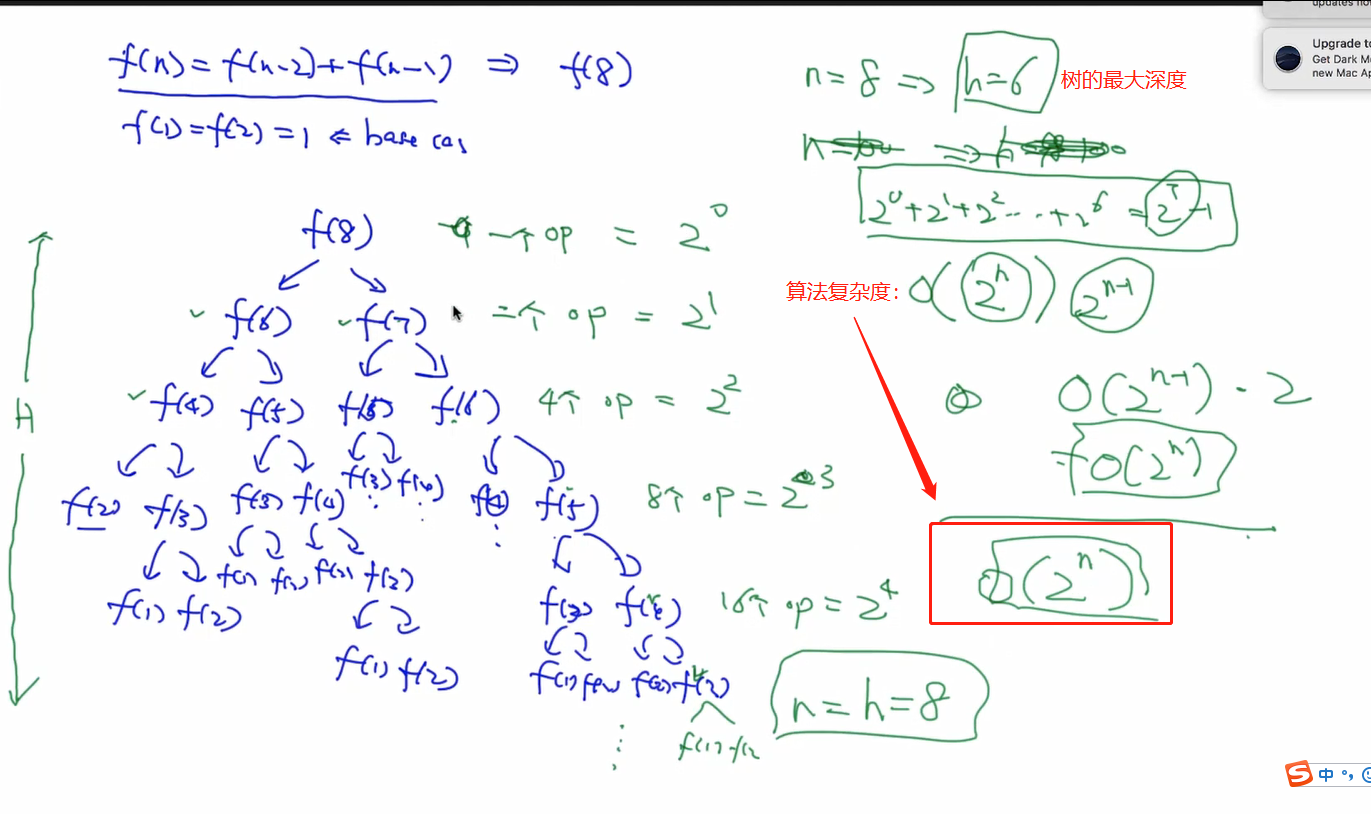
但是会发现计算了很多重复的例如f(3)等等。所以 后面会讲 DP 的算法可以存储中间的数据,不用重复计算。
斐波那契的空间复杂度:

动态规划:

# 时间复杂度? import numpy as np def fib(n): tmp = np.zeros(n) tmp[0] = 1 tmp[1] = 1 for i in range(2,n): tmp[i] = tmp[i-2]+tmp[i-1] return tmp[n-1] O(N) O(2^n) def fib(n): tmp = np.zeros(n) tmp[0] = 1 tmp[1] = 1 for i in range(2,n): tmp[i] = tmp[i-2]+tmp[i-1] return tmp[n-1] def fib(n): a,b=1,1 c =0 for i in range(2,n): c = a + b a = b b = c return c 思考题: 怎么在O(1)的时间复杂度下计算FIB(N)? 套公式 思考题: 这个公式怎么得来的? 提示: 转换成矩阵的连乘的形式, 矩阵连乘可以简化(MATRIX DECOMPOSION)
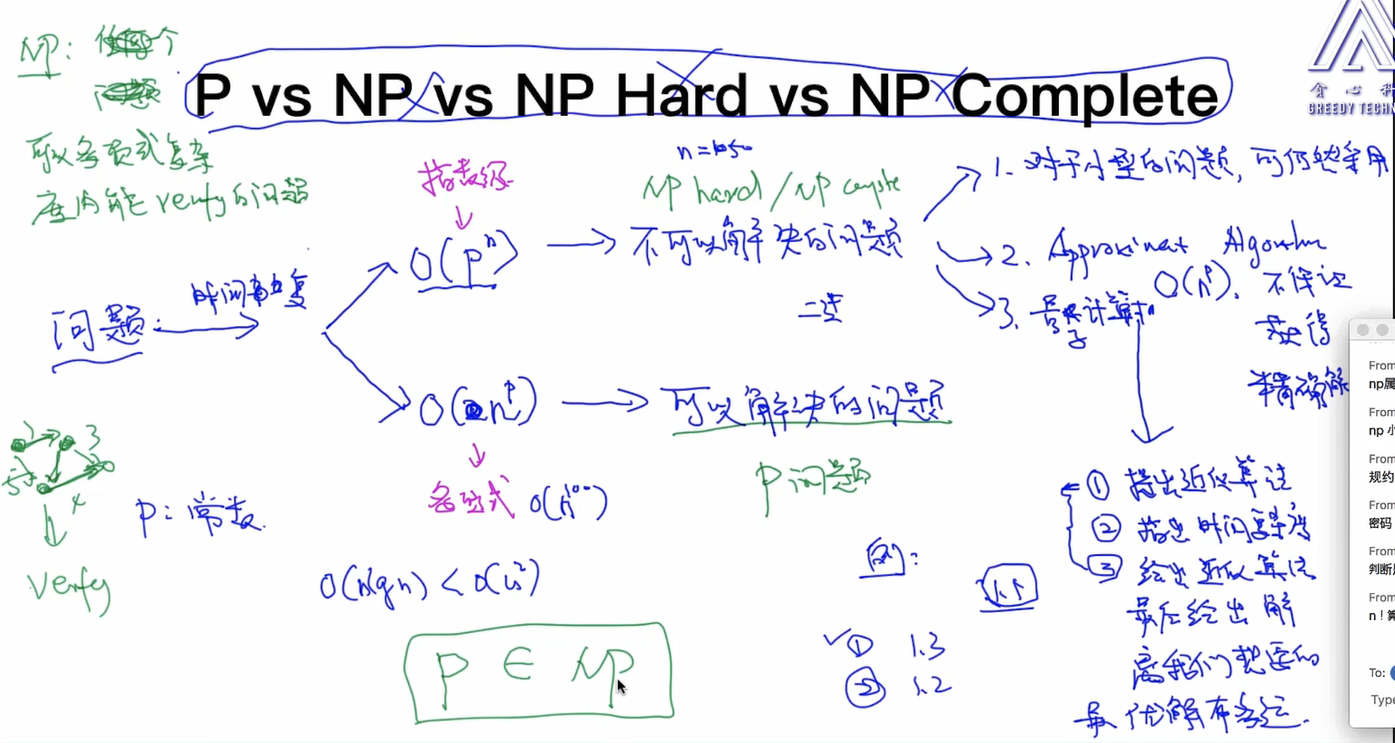
简单介绍一下:
P问题:
一个问题可以在多项式(O(n^k))的时间复杂度内解决。
NP问题:
一个问题的解可以在多项式的时间内被验证。
NP-hard问题:
任意np问题都可以在多项式时间内归约为该问题,但该问题本身不一定是NP问题。归约的意思是为了解决问题A,先将问题A归约为另一个问题B,解决问题B同时也间接解决了问题A。
NPC问题:
既是NP问题,也是NP-hard问题。
时间复杂度并不是表示一个程序解决问题需要花多少时间,而是当问题规模扩大后,程序需要的时间长度增长得有多快。也就是说,对于高速处理数据的计算机来说,处理某一个特定数据的效率不能衡量一个程序的好坏,而应该看当这个数据的规模变大到数百倍后,程序运行时间是否还是一样,或者也跟着慢了数百倍,或者变慢了数万倍。不管数据有多大,程序处理花的时间始终是那么多的,我们就说这个程序很好,具有O(1)的时间复杂度,也称常数级复杂度;数据规模变得有多大,花的时间也跟着变得有多长,这个程序的时间复杂度就是O(n),比如找n个数中的最大值;而像冒泡排序、插入排序等,数据扩大2倍,时间变慢4倍的,属于O(n^2)的复杂度。还有一些穷举类的算法,所需时间长度成几何阶数上涨,这就是O(a^n)的指数级复杂度,甚至O(n!)的阶乘级复杂度。不会存在O(2*n^2)的复杂度,因为前面的那个“2”是系数,根本不会影响到整个程序的时间增长。同样地,O (n^3+n^2)的复杂度也就是O(n^3)的复杂度。因此,我们会说,一个O(0.01*n^3)的程序的效率比O(100*n^2)的效率低,尽管在n很小的时候,前者优于后者,但后者时间随数据规模增长得慢,最终O(n^3)的复杂度将远远超过O(n^2)。我们也说,O(n^100)的复杂度小于O(1.01^n)的复杂度。
容易看出,前面的几类复杂度被分为两种级别,其中后者的复杂度无论如何都远远大于前者:一种是O(1),O(log(n)),O(n^a)等,我们把它叫做多项式级的复杂度,因为它的规模n出现在底数的位置;另一种是O(a^n)和O(n!)型复杂度,它是非多项式级的,其复杂度计算机往往不能承受。当我们在解决一个问题时,我们选择的算法通常都需要是多项式级的复杂度,非多项式级的复杂度需要的时间太多,往往会超时,除非是数据规模非常小。
P类问题的概念:如果一个问题可以找到一个能在多项式的时间里解决它的算法,那么这个问题就属于P问题。
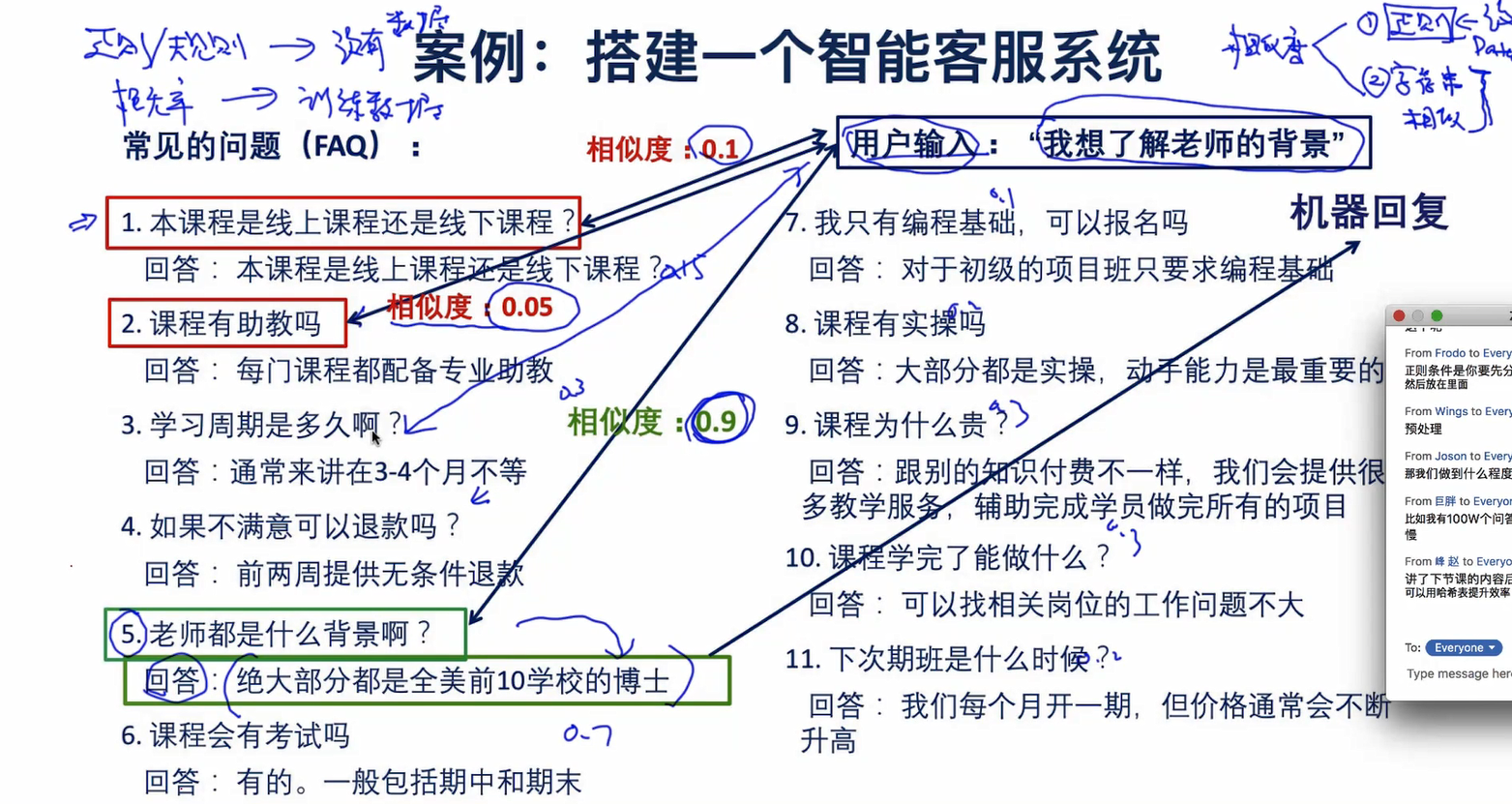
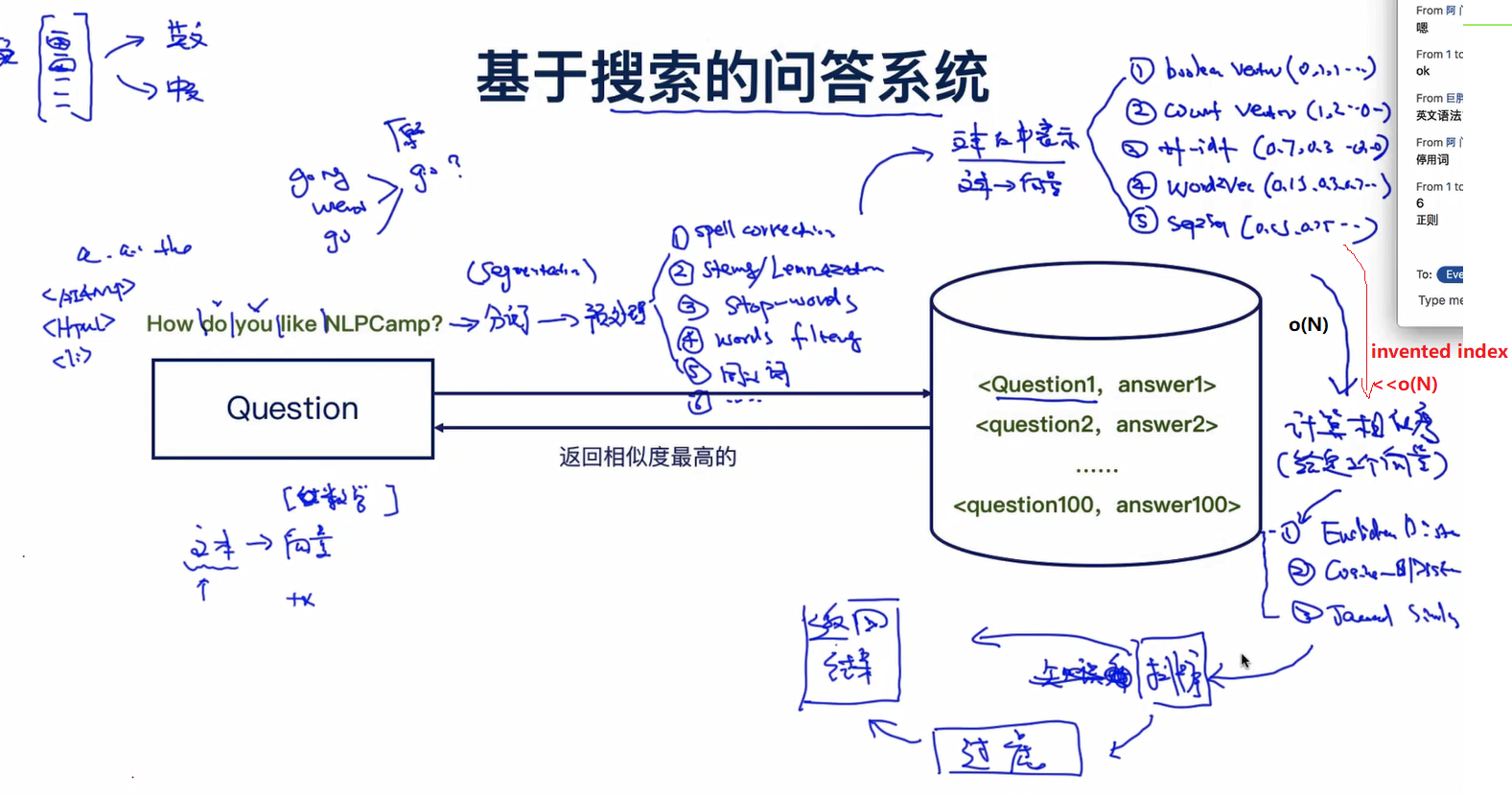




 浙公网安备 33010602011771号
浙公网安备 33010602011771号