计算几何
快考NOIP了我在这怼计算几何属于是脑子有点问题,随手记一下板子啥的得了,到时候有啥题目慢慢选上来
基础东西
(默认会向量求夹角,点积,叉积等东西)
向量类
(叉积用/只是习惯,懒得写cross了)
下文叙述为了方便也把/当向量积,*当数量积
1 struct point { 2 double x,y; 3 friend point operator - (const point &p1, const point &p2) { 4 return (point) {p1.x - p2.x, p1.y - p2.y}; 5 } 6 friend point operator + (const point &p1, const point &p2) { 7 return (point) {p1.x + p2.x, p1.y + p2.y}; 8 } 9 friend double operator * (const point &p1, const point &p2 { 10 return p1.x * p2.x + p1.y * p2.y; 11 } 12 friend double operator / (const point &p1, const point &p2) {// 叉积 13 return p1.x * p2.y - p2.x * p1.y; 14 } 15 }
精度处理
有的时候计算几何被卡精度了会十分难受,sgn是符号函数。
1 const double eps = 1e-8; 2 int sgn(double x) {return (x > eps) - (x < -eps);}
求两点之间的距离
勾股定理就好,但是这玩意不知道为啥就是容易写错。
1 double dist(point p1, point p2) { 2 return sqrt((p1.x - p2.x) * (p1.x - p2.x) + (p1.y - p2.y) * (p1.y - p2.y)); 3 }
也可以换种写法,不知道能不能更简洁。
1 double dist(point p1, point p2) { 2 point p = p1 - p2; 3 return sqrt(p * p); 4 }
判断点与直线的关系
用直线上一点到P的向量和直线的方向向量叉乘的正负来判定,顺指针(前一个向量转到后一个向量)负逆时针正。
1 int point_line(point x, point p1, point p2) {// p1 p2代表直线上两点 返回-1则点在直线上方 否则在下方 2 if(p1.x > p2.x) swap(p1, p2); 3 return sgn((x - p1) / (p2 - p1)); 4 }
判断两线段相交
需要通过快速排斥实验和跨立实验。
快速排斥实验简单来说就是确定两个最小长方形,包围住两个线段,如果这两个长方形都不相交那么两个线段一定不相交。实际上取线段横纵坐标的min/max来实现即可。
跨立实验就是通过叉积,判定两个点分别在这条线段所在直线的两侧。
由于只是所在直线,不代表线段无限延伸,所以要结合快速排斥实验判断。
同时也要注意某些题目是不是判断直线和线段相交。
1 bool intersect(point p1, point p2, point p3, point p4) {// p1p2 p3p4是两条线段 2 if(max(p1.x, p2.x) < min(p3.x, p4.x) || max(p3.x, p4.x) < max(p1.x, p2.x)) return 0; 3 if(max(p1.y, p2.y) < min(p3.y, p4.y) || max(p3.y, p4.y) < max(p1.y, p2.y)) return 0;// 快速排斥实验 4 double pro1 = (p4 - p1) / (p2 - p1); 5 double pro2 = (p3 - p1) / (p2 - p1); 6 return sgn(pro1) * sgn(pro2) <= 0;// 跨立实验 7 }
多边形面积
(遇到题再补代码)
最简单的想法是三角剖分后把面积加起来,但是太麻烦了。
其实直接求$\frac{1}{2} \sum_{i = 1}^{n} p_{i} / p_{i mod n + 1}$就好了。
随便找个多边形,画个图,向量积有正有负,这么转一圈就把多出来的部分抵消了。
极角排序
把所有点按与x轴的夹角大小排序,用叉积看正负即可(之前写的代码不是很严谨,理论上来说这里要用sgn判0)。
除了求凸包外还有一些神奇的作用,便于算贡献啥的。
bool cmp(const point &p1, const point &p2) {// 极角排序 记得与pt[1]距离为第二关键字 double mul = (p1 - pt[1]) * (p2 - p1); if(mul == 0) { point temp1 = p1 - pt[1], temp2 = p2 - pt[1]; return temp1 * temp1 < temp2 * temp2; } return mul > 0; }
这里的pt[1]是要极角排序的点中y最小的那个(有相同取x最小),同时要注意以距离为第二关键字,因为共线了有可能出现计算乱序的情况。
向量旋转
就是个公式。
1 point rotate(point p1, double a) {// 向量 逆时针 旋转a 弧度 2 return (point) {p1.x * cos(a) - p1.y * sin(a), p1.x * sin(a) + p1.y * cos(a); 3 }
凸包
能包含平面上所有给出点的最小周长的凸多边形叫凸包。
模板
graham法求凸包。andrew不会,咕了。
极角排序首先,拿个栈存当前已计算的凸包中的点,设栈中最后两个点p2,p1(前提是要有两个点,没有直接加入即可),新来的点p,如果(p1 - p2) * (p - p1) >= 0,那么代表当前凸包的切线还是在沿逆时针方向转动(或者没转)的。
否则可能就来了个比较远的点,需要一直弹栈弹到这个向量积>=0为止(或者说点不够了)。
时间复杂度$O(nlogn)$,瓶颈在极角排序。
1 sta[++top] = pt[1]; 2 sort(pt + 2, pt + n + 1, cmp); 3 for(int i = 2; i <= n; ++i) { 4 while((sta[top] - sta[top - 1]) * (pt[i] - sta[top]) <= 0 && top >= 2) --top; 5 sta[++top] = pt[i]; 6 } 7 sta[++top] = pt[1];
(简洁)
cmp是极角排序,pt[1]是初始点,取点规则如极角排序那里所述,就是找个y最小,y相同x最小的点。
最后加入pt[1]是方便计算,有的题目不能多加入,比如闵可夫斯基和。
叉积那里是<=0还是<0也要讨论,如果是<0那么就意味着要保留凸包上所有点而不是只保留关键点(拐角处)。
模板题在这,求二维凸包的周长。
SHOI2012 信用卡凸包
首先看subtask和样例明显是要我们思考没有圆弧(r=0)咋做。
就是把所有圆心整起来跑二维凸包模板求周长就好了,需要向量旋转公式。
考虑加上圆弧咋做,研究样例3。
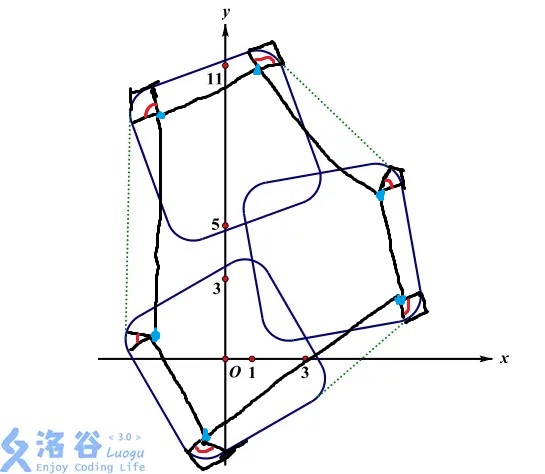
(图乱画的)
首先所有蓝色点表示弧圆心,黑色线要么是圆心到圆弧的辅助线半径,要么是所有圆心凸包上的线。
首先不看圆弧,拿圆心跑凸包,求出来那些黑色线(不是半径)长度之和。
我们发现剩下的圆弧就是所有红色标出来的圆心角所对圆弧之和(不是废话吗。。。)。
但是别急,这样做有什么好处呢?
我们感性理解一下,就是垂直于同一边的黑色辅助线是平行的,我们假想有一条边,在圆心凸包和实际凸包之间转,绕过所有红色标出圆心角,能感觉到这条边正好转了一周也就是三百六十度!
也就是答案=圆心凸包周长+$2 \pi r$。
具体怎么证明呢?
把切点按真实凸包线方向延长形成一系列交点,这些交点形成一个更大的凸多边形(如图所示)。
切线和半径成角90度,所以所有圆心角之和+凸多边形内角和=凸多边形角数量*180
设凸多边形n条边也即n个角,由于我们知道凸多边形内角和=(n-2)*180
把凸多边形内角和减过去,得圆心角之和=360,得证。
平面最近点对
分治法懒得介绍了,网上一抓一大把,我们来介绍性价比最高的“人类智慧”算法。本质上是一种乱搞,但是正确率高得离谱(可以直接认为100%正确率),代码、思想简易。
参考洛谷上的最高赞题解,这个是改进版的人类智慧法,原本只按x排序。
“我们充分发扬人类智慧:将所有点全部绕原点旋转同一个角度,然后按 x*y 排序。根据数学直觉,在随机旋转后,答案中的两个点在数组中肯定不会离得太远,所以我们只取每个点向前的 50 个点来计算答案。”
由于随机旋转的存在,出题人想卡你只能把ctime库给删了然后对着随机数种子卡,也就是说根本没法卡这个做法。
排序+一个循环+计算距离,就不用贴代码了吧。。。
旋转卡壳
(旋转卡壳有16种读音,你知道吗?)
模板
平面最近点对你会了,那你现在会平面最远点对吗?
(当然这个题是可以人类智慧乱搞过去的。。。)
首先用反证法可以证明,最远点对一定在凸包上。
然后我们就要引入一种线性的算法——旋转卡壳。
就是枚举凸包上的点对同时维护一些点,来求解一些(具体我还归纳不出来)题目。
这些凸包上点对往往有优美性质,能做到线性复杂度枚举。
我们枚举凸包一条边和一个点,同时维护到这条边的最远点,发现边逆时针转的同时这个点一定也是在逆时针转的。
点和我们枚举的边构成三角形同底,比较距离用叉积算面积就好了。
注意这里为了方便枚举是要把st[1]再加入栈中的,而且计算的最远点到了数组最后一项必须要切换回第一项,不然这个最远点就不更新了。
1 if(top == 3) printf("%d", dist(sta[1], sta[2])); 2 else { 3 for(int i = 1, j = 3; i < top; ++i) { 4 while(tri(sta[i], sta[i + 1], sta[j]) < tri(sta[i], sta[i + 1], sta[j + 1])) { 5 ++j; 6 if(j == top + 1) j = 1; 7 } 8 ans = max(ans, max(dist(sta[i], sta[j]), dist(sta[i + 1], sta[j]))); 9 } 10 printf("%d", ans); 11 }
HNOI2007 最小矩形覆盖
题目链接 求出能覆盖所有给出点的最小面积的矩形。
一般这种什么最远点对,最小覆盖,最大面积就是旋转卡壳了。
首先我们知道,覆盖所有点等价于覆盖掉凸包上所有的点,可以想象用一个最小的矩形“卡”住凸包,由此想到旋转卡壳。
首先我们枚举边,要覆盖所有点自然而然要维护距离这条边最远的点j(这里只是给凸包上的点编个号方便讨论,不然每次都打下标要累死人了)。只维护最远的点还不够,为了卡住所有点,还要维护“最左”的点l和”最右”的点r。
这个“最左”,“最右”怎么体现呢?这是一个关键的问题。
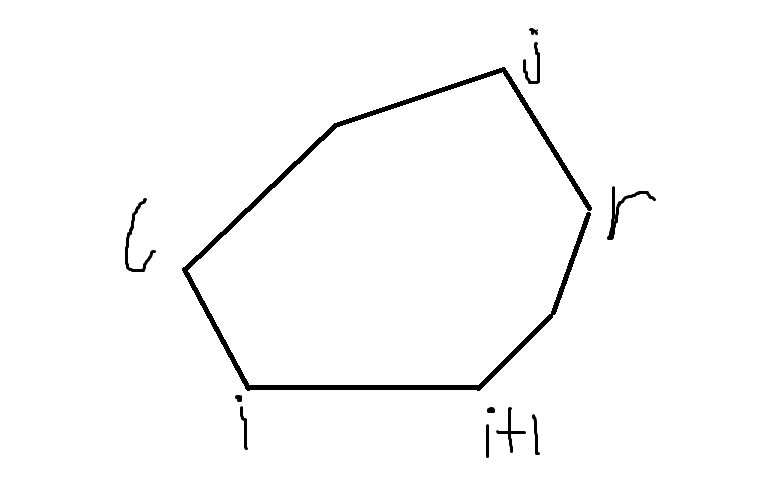
假设给出了i我们通过瞪大眼观察的办法就很容易瞪出来l是哪个,r是哪个,依据是什么呢?
假如我们加上坐标轴:
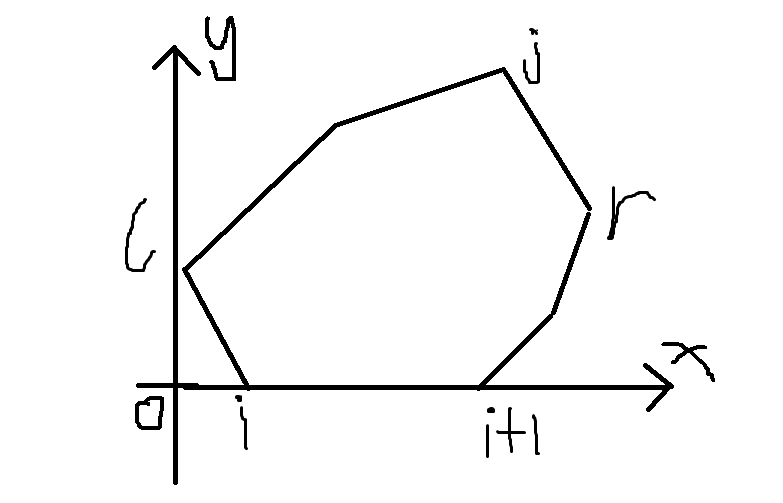
我们就有了一个合理的依据:x坐标最大的是r,x坐标最小的是l。
当然,现在$\overrightarrow{p_{i}p_{i+1}}$是在x轴上的,也就是水平的,假如它是斜的要怎么办呢?
这就不难想到投影了。
根据高中数学有$\vec{a}$在$\vec{b}$上的投影长度(其实带正负 表示投影向量方向)为$|\vec{a}|cos<\vec{a}, \vec{b}> = \frac{\vec{a} * \vec{b}}{|\vec{b}|}$,而本题目中讨论的投影都是投在$\overrightarrow{p_{i}p_{i+1}}$上的,也就是分母都是一样的正数,比大小的时候直接消掉了,只用比点积的大小。
r是满足$\overrightarrow{p_{i}p_{r}} * \overrightarrow{p_{i}p_{i+1}}$最大的那个点,l是满足$\overrightarrow{p_{i}p_{l}} * \overrightarrow{p_{i}p_{i+1}}$最小的那个点,l和r是可以和i或者i+1号点重合的。
j的维护办法跟上一题一样,r的话我们就比较一下r+1和r按上面式子整出来的点积大小,r+1更大就++r,l同理。
r的初值我们可以设置为2,但是l的初始值不好找,就按上面图的例子来说,l初始值设置为2的话他就卡在那里动不了了,后面的点怎么投影都要大一点。
怎么办呢?直觉上我们要把l的初始值设置为一个较中间的值,“中间”又不好把控。但是r已经走到了投影最大的位置,也就是说,r再往前走投影就会变小,这不就正好符合l初始值的要求吗?所以,我们把l的初始值设置为第一次找到的r就可以了。
这道题要把具体的点算出来,接下来就是烦人的高中数学环节了(虽然理论上来说高中数学没有叉积),拿出草稿纸推一推,不是难事。
设$p_{i} / p_{i+1} / p_{l} / p_{j} / p_{r}$分别为A、B、C、D、E,原点为O,方便讨论。
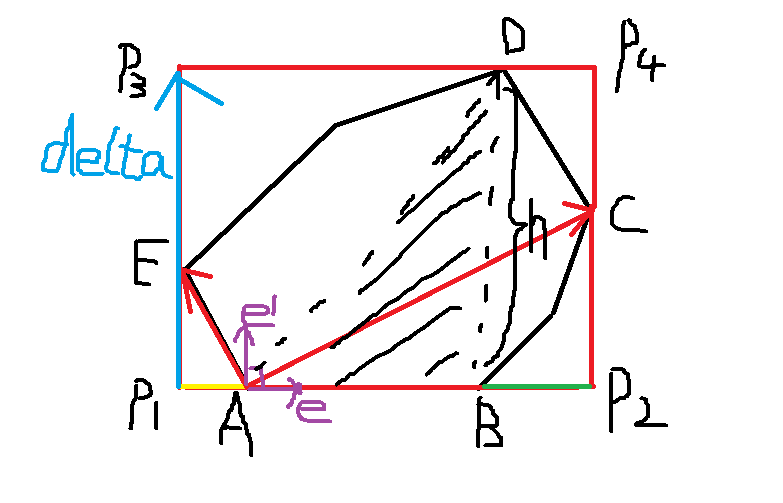
首先算出AB的长度len,$\overrightarrow{AB}$方向上的单位向量$\vec{e} = \frac{\overrightarrow{AB}}{len}$。
用$\overrightarrow{AE}$和$\overrightarrow{BC}$(图里面画错了)在$\overrightarrow{AB}$上投影,就可以算出$\overrightarrow{P_{1}A}$,$\overrightarrow{BP_{2}}$,长度分别对应黄色线段和绿色线段,注意这里把向量算出来,方便定位,可以直接用之前算出来的len。这样就得到了$P_{1}$,$P_{2}$的坐标
然后就是把矩形的高算出来,黑色斜线部分面积的两倍就是$\overrightarrow{AB} × \overrightarrow{AD}$(凸包枚举保证了逆时针,取绝对值也可以)。因此$h = \frac{\overrightarrow{AB} × \overrightarrow{AD}}{len}$。
$\vec{e}$逆时针旋转90度(符合凸包枚举顺序)得到向量$\vec{e'}$,便于定方向,设$\vec{e} = (x, y)$,则$\vec{e'} = (-y, x)$,旋转公式(甚至不需要,解一下点积为0模长相同就出来了)搞一搞就出来了。向量$\vec{\delta} = h\vec{e'}$,$\overrightarrow{OP_{3}} = \overrightarrow{OP_{1}} + \vec{\delta}$ , $P_{4}$同理。这样就得到了四个点坐标。
最后$\overrightarrow{P_{1}P_{2}} × \overrightarrow{P_{1}P_{3}}$即可得到矩形面积。答案输出嫌麻烦就直接极角排序一波就好了(其实没必要,排序方式跟graham求凸包一样的)。
1 void rotating_calipers() { 2 for(int i = 1, l = 2, r = 2, j = 3; i < top; ++i) { 3 while(pro1(sta[i], sta[i + 1], sta[j + 1]) >= pro1(sta[i], sta[i + 1], sta[j])) { 4 ++j; 5 if(j == top) j = 1; 6 } 7 while(pro2(sta[i], sta[i + 1], sta[r + 1]) >= pro2(sta[i], sta[i + 1], sta[r])) { 8 ++r; 9 if(r == top) r = 1; 10 } 11 if(i == 1) l = r;// 注意 12 while(pro2(sta[i], sta[i + 1], sta[l + 1]) <= pro2(sta[i], sta[i + 1], sta[l])) { 13 ++l; 14 if(l == top) l = 1; 15 } 16 point np1, np2, np3, np4; 17 point A = sta[i], B = sta[i + 1], C = sta[r], D = sta[j], E = sta[l]; 18 double len = sqrt((B - A) * (B - A)); 19 point e = (B - A) * (1 / len); 20 point f = e * ((A - E) * (B - A) / len); 21 point g = e * ((C - B) * (B - A) / len); 22 np1 = A - f; np2 = B + g; 23 double h = pro1(A, B, D) / len; 24 point _e = (point) {-e.y, e.x}; 25 point delta = _e * h; 26 np3 = np1 + delta; 27 np4 = np2 + delta; 28 if(pro1(np1, np2, np3) < S) { 29 S = pro1(np1, np2, np3); 30 p1 = np1, p2 = np2, p3 = np3, p4 = np4; 31 } 32 } 33 }
积分
模板
看到第一个函数你想这玩意不是可以积的吗,要啥自适应辛普森积分?
第二个显然就没啥办法了,这时候自适应辛普森积分就有用处了。
同时,这种用计算机算定积分近似值的办法可以推广到很多抽象的,无法具体用数学语言描述的函数,但是只要它能单点求值,被积的区间上连续,那么这个定积分的近似值就能求。
我们现在有一台计算机。你要算一个函数的积分。你的第一个想法是什么?
肯定是用定积分的定义暴力算啊!
但是画小矩形这种办法吧,他又慢,精度又低,有没有什么更好的办法呢?
还真有,一般被积的都是曲线,我们找个我们熟悉的,最简单的曲线去拟合它,也就是抛物线,把积分区间划分成一小段一小段,每一段当成二次函数来积分。
对于一个二次函数$f(x) = ax^{2} + bx + c$,有$\int^{r}_{l}f(x)dx = \frac{(r-l)(f(l) + 4f(\frac{l+r}{2}) + f(r))}{6}$(辛普森公式),因此函数只要能做到单点求值就可以近似地进行定积分。
但是还有个问题,这个划分的段数到底要怎么定?多了会TLE,少了精度不够会WA掉。
于是自适应辛普森法就出来了。具体地,我们递归地计算积分,对$[l, \frac{l+r}{2}]$,$[\frac{l+r}{2},r]$分别用辛普森公式算出他们的积分值al,ar,在此之前我们要对$[l, r]$用辛普森公式算出其积分值nans,如果al+ar和nans相差小于精度要求,那就可以返回值了,否则递归地计算$[l, \frac{l+r}{2}]$,$[\frac{l+r}{2},r]$的积分值并加起来。需要注意的是,如果一开始精度误差要求eps,递归时要将其除以2。
代码如下:
1 double f(double x) {// 这是被积函数 2 return ......; 3 } 4 double simpson(double l, double r) { 5 double mid = (l + r) / 2; 6 return (f(l) + 4 * f(mid) + f(r)) * (r - l) / 6; 7 } 8 double jifen(double l, double r, double neps, double nans) { 9 double mid = (l + r) / 2; 10 double al = simpson(l, mid), ar = simpson(mid, r); 11 if(fabs(al + ar - nans) < eps) return al + ar; 12 return jifen(l, mid, neps / 2, al) + jifen(mid, r, neps / 2, ar); 13 } 14 // 主函数调用jifen(l, r, eps, simpson(l, r))即可得到答案
模板1就水过去了。
由于我学高数的时候摸鱼去了,不会反常积分的审敛,所以模板2参考题解了,a<0积分发散,否则收敛。这里有个要注意的点就是反常积分的收敛性不能用函数的单点极限来判断。
经过测试上界取14,eps取1e-7就够了。
圆的面积并
题目链接 (原BZOJ2178,但是BZOJ已死)
我们f(x0)表示在x=x0直线处,所有圆和这条直线交线长度,圆的面积并就可以看做这个函数的积分,这个玩意显然是可以用区间合并来单点求的。
但是,完了吗?
需要注意的是我们要求函数连续,但是这个东西不一定连续,如果我们最开始5个点(计算[l, r], [l, mid], [mid, r])的单点求值都踩空了,那就完蛋了,积出来就是0。
所以我们还要在横坐标上做一次区间合并,一段一段地积分。
但是,还有高手?
考虑如下数据:
4 -3 0 1 -1 0 1 1 0 1 3 0 1
你会发现这玩意最开始单点求值也都踩空了。
怎么办呢?随机旋转一下所有圆心就好了。
贴一下f(x)计算的代码,其他和板子没啥区别,就多了个旋转,x轴上区间合并(与计算f(x)差不多的)。
1 struct segment { 2 double l,r; 3 friend bool operator < (const segment &s1, const segment &s2) { 4 return s1.l < s2.l; 5 } 6 }xs[1005],ys[1005],xs2[1005],ys2[1005]; 7 int n,xtop,ytop; 8 double x[1005],y[1005],r[1005],theta,ans; 9 double f(double xi) { 10 double ret = 0; 11 ytop = 0; 12 for(int i = 1; i <= n; ++i) { 13 if(sgn(fabs(xi - x[i]) - r[i]) == 1) continue; 14 double len = sqrt(r[i] * r[i] - (xi - x[i]) * (xi - x[i])); 15 ys[++ytop] = (segment) {y[i] - len, y[i] + len}; 16 } 17 sort(ys + 1, ys + ytop + 1); 18 int temp = ytop; 19 ytop = 0; 20 for(int i = 1; i <= temp; ++i) { 21 if(sgn(ys[i].l - ys2[ytop].r) == 1) ys2[++ytop] = ys[i]; 22 else ys2[ytop].r = max(ys2[ytop].r, ys[i].r); 23 } 24 for(int i = 1; i <= ytop; ++i) ret += ys2[i].r - ys2[i].l; 25 return ret; 26 }
扫描线
这里不建议观看,依托答辩。
模板
题目链接 求矩形的面积并。
有了上面的圆的面积并的做法,我们应该能意识到这个东西跟区间合并密切相关。但是,矩形挺规整的,又不是啥曲线,有什么上积分的必要吗?
所以我们就有了扫描线算法。
更多时候扫描线是一种数据结构题的做法,我的理解就是通过排序维护某一维度的偏序关系,这里不介绍了,典题见SDOI2009 HH的项链。
我们把矩形拆成俩竖线,记为入线和出线,把所有竖线按x坐标值排序,两条竖线之间面积贡献就是x坐标差乘上区间合并后区间总长。
同时需要动态地维护区间合并,支持插入线段,删除线段,查询区间合并总长。
既然是区间合并,那自然就能想到线段树维护,这个东西是显然具有结合律的。
xy很大,需要离散化。还有一个边界,就是线段树上修改的时候,右边界要取y离散化的值减1,从连续线段映射到离散会有这么一个转化,画画图就理解了。
1 sort(xian + 1, xian + (n << 1 | 1));//从左到右扫 2 // 离散化 3 sort(yv + 1, yv + (n << 1 | 1)); 4 limit = unique(yv + 1, yv + (n << 1 | 1)) - yv - 1; 5 build(1, 1, limit - 1); 6 for(int i = 1; i <= limit; ++i) lsh[yv[i]] = i; 7 for(int i = 1; i <= (n << 1); ++i) { 8 ans += t[1].len * (xian[i].x - xian[i - 1].x);// 统计答案 前面的是区间合并的总长 后面的是竖线之间的横坐标之差 9 change(1, lsh[xian[i].y1], lsh[xian[i].y2] - 1, xian[i].type);// 线段树更新区间合并 type = 1是入线 type = -1是出线 10 }
(扫描线没啥代码的原因主要是我之前写的代码依托答辩,就不贴了)
IOI1998 矩形周长picture
题目链接 求矩形的周长并。
比面积并麻烦一点,我们要分别计算横线、竖线的贡献。
竖线的贡献可以用更新前后区间合并的总长的差来计算,很好理解,竖线产生贡献不是哪里多了一块就是哪里少了一块。
横线的贡献就是2 * 。
注意线段树到叶子结点更新的问题,不判边界就要开16倍空间。
还有一个需要注意的是,处理的时候要按横坐标相同,先处理出线再处理入线的方式进行。
窗口的星星
要转化一下,每个星星对应一个区域,矩形右上角在这个区域内星星才能产生贡献。由于在边界上不算,我们不妨把矩形长宽都缩短0.5,区域就是(x,y)到(x + w - 1, y + h - 1)。
我们采用扫描线,现在就是转化成合并的区间(扫描线扫到的目前位置)上哪个点的值最大,区间加,用线段树也可以简单维护。
NOI2023 方格染色
题目保证最多只有5次斜线染色操作,明示做法:斜线暴力随便搞,其他转化为矩形面积并进行扫描线。
这题主要是斜线有点难搞。其实要计算的东西本质是斜线的并集对答案的贡献,不难想到容斥原理。
同时我们需要把斜线跟所有横竖线求一下交点,把交点的x坐标拿出来排序去重,然后减掉去重后的点数量,才是当前枚举的斜线的集合的贡献。
代码(容斥部分):
1 for(short st = 1; st <= (1 << k) - 1; ++st) { 2 int nx1 = 0, ny1 = 0, nx2 = 0, ny2 = 0; 3 for(short i = 1; i <= 5; ++i) { 4 if(!(st >> (i - 1) & 1)) continue; 5 if(!nx1) { 6 nx1 = x1s[bh[i]]; 7 ny1 = y1s[bh[i]]; 8 nx2 = x2s[bh[i]]; 9 ny2 = y2s[bh[i]]; 10 } 11 else {// 这是斜线求并集 比一般的区间合并麻烦点 12 if(ny1 - nx1 != y1s[bh[i]] - x1s[bh[i]]) { 13 nx1 = 0; 14 break; 15 } 16 if(nx2 < x1s[bh[i]]) { 17 nx1 = 0; 18 break; 19 } 20 if(nx1 > x2s[bh[i]]) { 21 nx1 = 0; 22 break; 23 } 24 nx1 = max(nx1, x1s[bh[i]]); 25 ny1 = max(ny1, y1s[bh[i]]); 26 nx2 = min(nx2, x2s[bh[i]]); 27 ny2 = min(ny2, y2s[bh[i]]); 28 } 29 } 30 if(nx1) {// 奇容偶斥一样的 31 if(popcnt(st) & 1) ans += nx2 - nx1 + 1; 32 else ans -= nx2 - nx1 + 1; 33 top = 0; 34 for(int i = 1; i <= q; ++i) { 35 if(ts[i] == 3) continue; 36 if(ts[i] == 1 && y1s[i] >= ny1 && y1s[i] <= ny2) {// 跟横线求交 37 int jx = y1s[i] - ny1 + nx1; 38 if(jx >= x1s[i] && jx <= x2s[i]) yys[++top] = jx - nx1 + ny1; 39 } 40 if(ts[i] == 2 && x1s[i] >= nx1 && x1s[i] <= nx2) {// 跟竖线求交 41 int jy = x1s[i] - nx1 + ny1; 42 if(jy >= y1s[i] && jy <= y2s[i]) yys[++top] = jy; 43 } 44 } 45 sort(yys + 1, yys + top + 1); 46 top = unique(yys + 1, yys + top + 1) - yys - 1; 47 if(popcnt(st) & 1) ans -= top;// 最后减掉才是真正贡献 48 else ans += top; 49 } 50 }
最小圆覆盖
模板
引理:若点 $p$ 不在集合 $S$ 最小覆盖圆内,则点 $p$ 一定在集合 $S \bigcup {p}$ 的最小覆盖圆上。
然后我们就有一个暴力的办法:
枚举点,如果当前点在最小覆盖圆内,跳过,否则该点一定在圆上,再回头找在圆上的两个点。
固定一个点后,从头开始往后找第一个不在圆上的点 $q$,把当前圆心设为 $p$ 和 $q$ 中点,继续找下一个点。
固定两个点后,从头开始往后找第一个不在圆上的点 $r$,求解$p$,$q$,$r$ 的外接圆圆心作为目前圆心。
可以用概率证明(不太会)随机数据情况下这样做时间复杂度 $O(n)$,数据不随机就 $random_shuffle$ 一下就行了,因为这里主要是看顺序随不随机。
求解外接圆就草稿纸上列方程然后消元即可。
1 struct point { 2 double x,y; 3 }p[100005],O; 4 void random_shuffle_(point *a, int len) { 5 for(int i = 1; i <= len; ++i) swap(a[rnd() % len + 1], a[rnd() % len + 1]); 6 } 7 bool incircle(point p1) { 8 return (p1.x - O.x) * (p1.x - O.x) + (p1.y - O.y) * (p1.y - O.y) <= r + eps; 9 } 10 void wjy(point p1, point p2, point p3) {// 外接圆,解方程 11 double a1 = p2.x - p1.x, a2 = p3.x - p1.x; 12 double b1 = p2.y - p1.y, b2 = p3.y - p1.y; 13 double c1 = (p2.x * p2.x - p1.x * p1.x + p2.y * p2.y - p1.y * p1.y) / 2; 14 double c2 = (p3.x * p3.x - p1.x * p1.x + p3.y * p3.y - p1.y * p1.y) / 2; 15 O.x = (b2 * c1 - b1 * c2) / (b2 * a1 - b1 * a2); 16 O.y = (a2 * c1 - a1 * c2) / (a2 * b1 - a1 * b2); 17 r = (O.x - p1.x) * (O.x - p1.x) + (O.y - p1.y) * (O.y - p1.y); 18 } 19 void work() { 20 O.x = 0; O.y = 0; r = 0; 21 for(int i = 1; i <= n; ++i) { 22 if(incircle(p[i])) continue; 23 O = p[i]; r = 0; 24 for(int j = 1; j <= i - 1; ++j) { 25 if(incircle(p[j])) continue; 26 O = (point) {(p[i].x + p[j].x) / 2, (p[i].y + p[j].y) / 2}; 27 r = (p[i].x - p[j].x) * (p[i].x - p[j].x) + (p[i].y - p[j].y) * (p[i].y - p[j].y); 28 r = r / 4; 29 for(int k = 1; k <= j - 1; ++k) { 30 if(incircle(p[k])) continue; 31 wjy(p[i], p[j], p[k]); 32 } 33 } 34 } 35 }
[SHOI2014] 信号增幅仪
求最小椭圆覆盖,椭圆还是斜的。
考虑转化到新的坐标系 $x'oy$ 里面做,我们把旋转和拉伸的影响全部消除就好了。
也就是把所有点顺时针旋转 $a°$ 后横坐标都乘以 $\frac{1}{p}$ 之后做最小圆覆盖就行了。
半平面交
摆






 浙公网安备 33010602011771号
浙公网安备 33010602011771号