对两个独立且均匀分布的随机变量进行三角函数运算

1. 前提

假设变量\(\alpha\)，\(\beta\)彼此独立，且均匀分布于\([0,2\pi]\)内，已知联合分布\(f(\alpha,\beta)\)满足

\[ f(\alpha,\beta) = \left\{ \begin{aligned} &\frac{1}{4\pi^2} \quad && \alpha\in[0,2\pi],\beta\in[0,2\pi],\\ &0 && \text{otherwise}. \end{aligned} \right. \]

现在给定以下，

\[\begin{aligned} M(\underbrace{\cos(\frac{\alpha+\beta}{2})}_{\text{Term 1}}\cos(\frac{\alpha-\beta}{2}),\underbrace{\sin(\frac{\alpha+\beta}{2})}_{\text{Term 2}}\underbrace{\cos(\frac{\alpha-\beta}{2}))}_{\text{Term 3}}. \end{aligned} \]

求对应元素的概率分布函数（PDF）及累计分布函数（CDF）。

2. 准备

假设 \(z_1 = \frac{\alpha+\beta}{2}\), 我们可以获得对应的雅各比矩阵 \(J_1\) 形如

\[ \begin{aligned} &0 \leq && t_1= \alpha &&\leq 2\pi,\\ &0 \leq && t_2= 2Z - \alpha &&\leq 2\pi, \end{aligned} \]

源于\(J_1 = \begin{vmatrix} \frac{\partial t_1}{\partial \alpha}&\frac{\partial t_1}{\partial z_1}\\ \frac{\partial t_2}{\partial \alpha}&\frac{\partial t_2}{\partial z_1} \end{vmatrix} = \begin{vmatrix} 1&0\\-1&2 \end{vmatrix}\) 且 \(|J_1| = 2\)。 并且推导 \(z_1\) 的PDF为

\[ \begin{aligned} f_{Z_1}(z_1) =\left\{ \begin{aligned} &\int_{0}^{2z_1} \frac{2}{4\pi^2}d \alpha= \frac{z_1}{\pi^2} &&z_1\in[0,\pi),\\ &\int_{2z_1 - 2\pi}^{2\pi} \frac{2}{4\pi^2}d \alpha= \frac{2\pi - z_1}{\pi^2} &&z_1\in[\pi,2\pi],\\ & 0 && \text{otherwise}. \end{aligned} \right. \end{aligned} \]

由此可得 \(z_1\)的PDF,

\[ \begin{aligned} F(z_1) =\left\{ \begin{aligned} & 0 &&z_1\in(-\infty,0),\\ &\frac{z_1^2}{2\pi^2} &&z_1\in[0,\pi),\\ &\frac{2z_1}{\pi}-\frac{z^2_1}{2\pi^2}-1 &&z_1\in[\pi,2\pi],\\ & 1 &&z_1\in(2\pi,\infty).\\ \end{aligned} \right. \end{aligned} \]

3. Term 1

3.1 解析解

定义 \(u = U = \cos(z_1)\), 且 \(z_1 = \arccos (u), u\in[-1,1]\)，可得

\[\frac{d z_1}{d u}=-\frac{1}{\sqrt{1-u^2}}. \]

对应\(u\)的CDF可得

\[ \begin{aligned} F(u) &= P\{ U\leq u \} = P\{\cos(z_1)\leq u\}\\ &= P\{\arccos(u)\leq z_1 \leq 2\pi-\arccos(u)\}\\ &= \frac{2(2\pi - \arccos(u))}{\pi}-\frac{(2\pi - \arccos(u))^2}{2\pi^2}\\ &\quad -1-\frac{(\arccos(u))^2}{2\pi^2}\\ &= \frac{\pi^2-(\arccos(u))^2}{\pi^2}. \end{aligned} \]

由此对应\(u\)的PDF可得

\[ \begin{aligned} f_{U}(u) =\left\{ \begin{aligned} & \frac{2 \arccos(u)}{\pi^2 \sqrt{1-u^2}} &&u\in[-1,1]\\ &0 && \text{otherwise}. \end{aligned} \right. \end{aligned} \]

对应\(u\)的期望可得

\[ \begin{aligned} \mathbf{E}[u] =\mathbf{E}[\cos(\frac{\alpha+\beta}{2})]= \int_{-1}^1 u f_U(u) du = -0.4053. \end{aligned} \]

3.2 Matlab代码验证

%% U = u = cos((a+b)/2) simulation
figure(1);clf; hold on;
% number = 5000000;
number = 10000;
for i = 1 : number
    a = unifrnd(0, 2 * pi);
    b = unifrnd(0, 2 * pi);
    c(i) = cos((a+b)/2);
end
cdfplot(c)
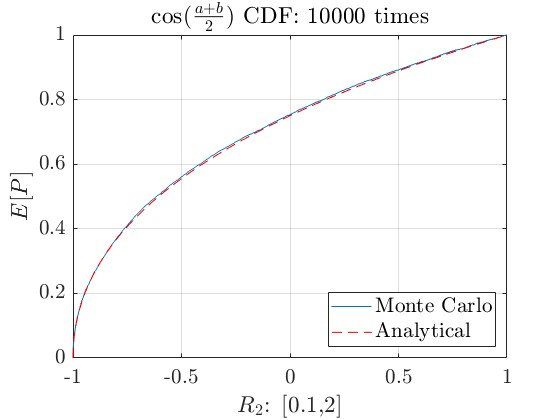
str1 = ['$\cos(\frac{a+b}{2})$ CDF:' num2str(number) ' times'];
title(str1,'interpreter','latex','FontSize',16);

% CDF of Analytical U
fplot(@(x) 1-(acos(x))^2/pi^2,[-1 1],'r--')
str1 = ['$\cos(\frac{a+b}{2})$ CDF:' num2str(number) ' times'];
title(str1,'interpreter','latex','FontSize',16);

4. Term 2

4.1 解析解

定义 \(v = V = \sin(z_1)\), 且 \(z_1 = \arcsin (u), v\in[-1,1]\)，可得

\[\frac{d z_1}{d v}=\frac{1}{\sqrt{1-v^2}}. \]

对应\(v\)的CDF可得

\[ \begin{aligned} F(v) &= P\{ V\leq v \} = P\{\sin(z_1)\leq v\}\\ &= P\{z_1\leq \arcsin(v)\\ &=\left\{ \begin{aligned} & 0 &&\quad \,z_1\in(-\infty,0),\\ & P\{z_1\leq \arcsin(v)\}+&&\\ & \quad P\{z_1\geq \pi - \arcsin(v)\} &&\quad \, z_1\in[0,\pi],\\ & P\{\pi - \arcsin(v) \leq z_1 \leq &&\\ & \quad 2\pi+\arcsin(v)\} &&\quad \,z_1\in[\pi,2\pi],\\ & 1 &&\quad \, z_1\in(2\pi,\infty).\\ \end{aligned} \right.\\ &=\left\{ \begin{aligned} & 0 &&v\in(-\infty,-1),\\ & \frac{\pi^2+2\pi \arcsin(v)}{2\pi^2} &&v\in[-1,1],\\ & 1 &&v\in(1,\infty).\\ \end{aligned} \right. \end{aligned} \]

由此对应\(v\)的PDF可得

\[ \begin{aligned} f_{V}(v) =\left\{ \begin{aligned} & \frac{1}{\pi \sqrt{1-v^2}} &&v\in[-1,1],\\ &0 && \text{otherwise}. \end{aligned} \right. \end{aligned} \]

对应\(v\)的期望可得

\[ \begin{aligned} \mathbf{E}[v] =\mathbf{E}[\sin(\frac{\alpha+\beta}{2})] = \int_{-1}^1 v f_V(v) dv = 0. \end{aligned} \]

4.2 Matlab代码验证

%% V = v = sin((a+b)/2) simulation
figure(3);clf; hold on;
for i = 1 : number
    a = unifrnd(0, 2 * pi);
    b = unifrnd(0, 2 * pi);
    d(i) = sin((a+b)/2);
end
cdfplot(d)
str1 = ['$\sin(\frac{a+b}{2})$ CDF:' num2str(number) ' times'];
title(str1,'interpreter','latex','FontSize',16);

% CDF of Analytical V
fplot(@(x) (pi^2+2*pi*asin(x))/(2*pi^2),[-1 1],'g--')
str1 = ['$\sin(\frac{a+b}{2})$ CDF:' num2str(number) ' times'];
title(str1,'interpreter','latex','FontSize',16);

5. Term 3

5.1 解析解

假设 \(z_2 = \frac{\alpha-\beta}{2}\), \(w = W = \cos(z_2)\)和\(\beta = \alpha - 2z_2\)，我们可以获得对应的雅各比矩阵 \(J_2\) 形如

\[ \begin{aligned} &0 \leq && t_3= \alpha &&\leq 2\pi,\\ &0 \leq && t_4= \alpha - 2z_2 &&\leq 2\pi, \end{aligned} \]

且 \(J_2 = \begin{vmatrix} \frac{\partial t_3}{\partial \alpha}&\frac{\partial t_3}{\partial z_1}\\ \frac{\partial t_4}{\partial \alpha}&\frac{\partial t_4}{\partial z_1} \end{vmatrix} = \begin{vmatrix} 1&0\\1&-2 \end{vmatrix}\) and \(|J_2| = 2\). 由此可得\(z_2\)的PDF为

\[ \begin{aligned} f_{Z_2}(z_2) =\left\{ \begin{aligned} &\int_{0}^{2z_2+2\pi} \frac{2}{4\pi^2}d \alpha = \frac{\pi+z_2}{\pi^2} &&z_2\in[-\pi,0),\\ &\int_{2z_2 }^{2\pi} \frac{2}{4\pi^2} d \alpha = \frac{\pi-z_2}{\pi^2}&&z_2\in[0,\pi],\\ & 0 && \text{otherwise}. \end{aligned} \right. \end{aligned} \]

可得\(z_2\)的CDF为

\[ \begin{aligned} F(z_2) =\left\{ \begin{aligned} & 0 &&z_2\in(-\infty,-\pi),\\ &\frac{2\pi z_2+z^2_2}{2\pi^2} &&z_2\in[-\pi,0),\\ &\frac{2\pi z_2-z^2_2}{2\pi^2} &&z_2\in[0,\pi],\\ & 1 &&z_2\in(\pi,\infty).\\ \end{aligned} \right. \end{aligned} \]

定义 \(w = W = \cos(z_2)\), 且 \(z_2 = \arccos (w), w\in[-1,1]\)，可得

\[\frac{d z_2}{d w}=-\frac{1}{\sqrt{1-w^2}}. \]

由此对应\(w\)的CDF可得

\[ \begin{aligned} F(w) &= P\{ W\leq w \} = P\{\cos(z_2)\leq w\}\\ &= P\{z_2\leq -\arccos(w)\}+ P\{z_2\geq \arccos(w)\}\\ &= 1 - P\{-\arccos(w)\leq z_2 \leq \arccos(w) \}\\ &= 1 - \frac{2\arccos(w)}{\pi}+\frac{(\arccos(w))^2}{\pi^2}. \end{aligned} \]

由此对应\(w\)的PDF可得

\[ \begin{aligned} f_{W}(w) =\left\{ \begin{aligned} & \frac{2}{\pi \sqrt{1-w^2}}- \frac{2\arccos(w)}{\pi^2\sqrt{1-w^2}} &&w\in[-1,1]\\ &0 && \text{otherwise}. \end{aligned} \right. \end{aligned} \]

对应\(w\)的期望可得

\[ \begin{aligned} \mathbf{E}[w] =\mathbf{E}[\cos(\frac{\alpha-\beta}{2})]= \int_{-1}^1 w f_W(w) dw = 0.4053. \end{aligned} \]

5.2 Matlab代码验证

figure(5);clf;hold on;
for i = 1 : number
    a = unifrnd(0, 2 * pi);
    b = unifrnd(0, 2 * pi);
    e(i) = cos((a-b)/2);
end
cdfplot(e)
str1 = ['$\cos(\frac{a-b}{2})$ CDF:' num2str(number) ' times'];
title(str1,'interpreter','latex','FontSize',16);


% CDF of Analytical W
fplot(@(x) (pi-acos(x))^2/(1*pi^2),[-1 1],'g--')
str1 = ['$\cos(\frac{a-b}{2})$ CDF:' num2str(number) ' times'];
title(str1,'interpreter','latex','FontSize',16);