数据结构之排序算法
一、分类
1.1 内部排序
一、插入排序
1.直接插入排序
2.折半插入排序
3.希尔排序
二、交换类排序
1.冒泡排序
2.快速排序
三、选择类排序
1.简单选择排序
2.堆排序
四、归并排序
二路归并排序
1.2 外部排序
归并排序
二、各排序详解
直接插入排序
public static void insertionSort(int[] a) {
int tmp;
for (int i = 1; i < a.length; i++) {
for (int j = i; j > 0; j--) {
if (a[j] < a[j - 1]) {
tmp = a[j - 1];
a[j - 1] = a[j];
a[j] = tmp;
}
}
}
}
折半插入排序
寻找插入的位置采用折半查找法
希尔排序
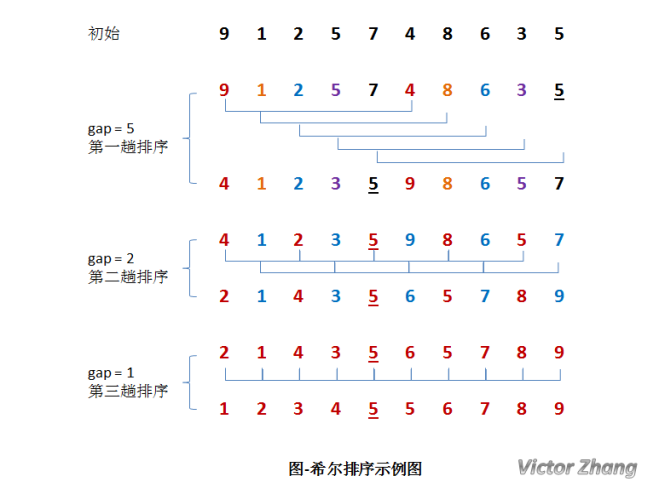
希尔(Shell)排序又称为缩小增量排序,它是一种插入排序。它是直接插入排序算法的一种威力加强版。
把记录按步长 gap 分组,对每组记录采用直接插入排序方法进行排序。随着步长逐渐减小,所分成的组包含的记录越来越多,当步长的值减小到 1 时,整个数据合成为一组,构成一组有序记录,则完成排序。gap1 = N / 2 ,gapk = gap(k-1) / 2
冒泡排序
public static void bubbleSort(int[] a) {
int flag;
int temp;
for (int i = a.length-1; i > 0; --i) {
flag = 0;
for (int j = 1; j <= i; ++j) {
if (a[j] < a[j - 1]) {
temp = a[j];
a[j] = a[j - 1];
a[j - 1] = temp;
flag = 1;
}
}
if(flag == 0)
return;
}
}
快速排序
public static void partition(int []array,int lo,int hi){
//固定的切分方式
int key=array[lo];
while(lo<hi){
while(array[hi]>=key&&hi>lo){
hi--;
}
array[lo]=array[hi];
while(array[lo]<=key&&hi>lo){
lo++;
}
array[hi]=array[lo];
}
array[hi]=key;
partition(int []array,lo, hi-1);
partition(int []array, lo, hi+1);
}
简单选择排序
public void selectionSort(int[] list) {
// 需要遍历获得最小值的次数
// 要注意一点,当要排序 N 个数,已经经过 N-1 次遍历后,已经是有序数列
for (int i = 0; i < list.length - 1; i++) {
int temp = 0;
int index = i; // 用来保存最小值得索引
// 寻找第i个小的数值
for (int j = i + 1; j < list.length; j++) {
if (list[index] > list[j]) {
index = j;
}
temp = list[index];
list[index] = list[i];
list[i] = temp;
printAll(list);
}
}
堆排序
① 先将初始文件R[1..n]建成一个大根堆,此堆为初始的无序区
② 再将关键字最大的记录R[1](即堆顶)和无序区的最后一个记录R[n]交换,由此得到新的无序区R[1..n-1]和有序区R[n],且满足R[1..n-1].keys≤R[n].key
③由于交换后新的根R[1]可能违反堆性质,故应将当前无序区R[1..n-1]调整为堆。然后再次将R[1..n-1]中关键字最大的记录R[1]和该区间的最后一个记录R[n-1]交换,由此得到新的无序区R[1..n-2]和有序区R[n-1..n],且仍满足关系R[1..n-2].keys≤R[n-1..n].keys,同样要将R[1..n-2]调整为堆。
……
直到无序区只有一个元素为止。
public class HeapSort {
/**
* 构建大顶堆 数组下标从1开始
*/
public static void adjustHeap(int[] a, int i, int len) {
int temp, j;
temp = a[i];
for (j = 2 * i; j <= len; j *= 2) {// 沿关键字较大的孩子结点向下筛选
if (j < len && a[j] < a[j + 1])
++j; // j为关键字中较大记录的下标
if (temp >= a[j])
break;
a[i] = a[j];
i = j;
}
a[i] = temp;
}
public static void heapSort(int[] a) {
int i;
for (i = a.length / 2; i > 0; i--) {// 构建一个大顶堆
adjustHeap(a, i, a.length);
}
for (i = a.length; i > 1; i--) {// 将堆顶记录和当前未经排序子序列的最后一个记录交换
int temp = a[1];
a[1] = a[i];
a[i] = temp;
adjustHeap(a, 1, i - 1);// 将a中前i-1个记录重新调整为大顶堆
}
}
public static void main(String[] args) {
int a[] = { 51, 46, 20, 18, 65, 97, 82, 30, 77, 50 };
heapSort(a);
System.out.println(Arrays.toString(a));
}
}
二路归并排序(内部)

K路归并排序(外部)
外部排序指的是大文件的排序,即待排序的记录存储在外存储器上,待排序的文件无法一次装入内存,需要在内存和外部存储器之间进行多次数据交换,以达到排序整个文件的目的。外部排序最常用的算法是多路归并排序,即将原文件分解成多个能够一次性装入内存的部分,分别把每一部分调入内存完成排序。然后,对已经排序的子文件进行归并排序。
过程 :
1.初始归并段生成
将文件分段输入内存并排序,排序完的文件称归并段,将其写入外存,这样就形成了许多初始归并段。
置换-选择排序
文件输入记录,当填满缓冲区后,选择最小记录输出,空缺位置由下个输入记录取代,输出记录即为初始归并段的一部分。(新填充的记录如果不能成为当前归并段的一部分,也就是说比当前归并段最大记录小,那么等待下一个归并段提供选择)
2.最佳归并树建立
二路归并即用哈夫曼树,I/O次数 = 带权路径长度*2。
三、复杂度与稳定性
3.1 时间复杂度
平均情况
快速排序、希尔排序、堆排序、归并排序 O(log2n)
其他的为O(n平方)
最坏情况
快排为O(n平方),越无序越好
其他和平均情况一样
最好情况
有序的情况下,直接插入排序和冒泡排序为O(n)
3.2 空间复杂度
快排为O(log2n)
归并排序为O(n)
3.3 稳定性
快速排序、希尔排序、简单选择排序、堆排序为不稳定的
其余为稳定的



 浙公网安备 33010602011771号
浙公网安备 33010602011771号