课堂作业第三阶段

题目:返回一个二维整数数组中最大子数组的和。

如：

 

 

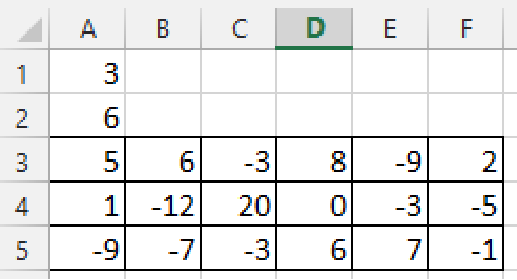
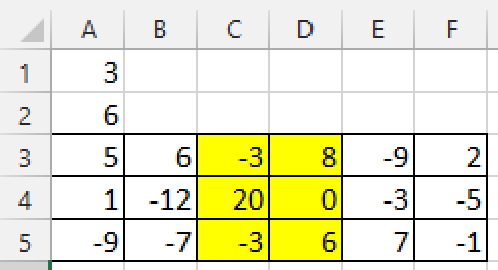
输出：28

本题的思路：我的思路是因为题目要求求出最大子矩阵，那么矩阵的确定可由左上角的坐标和右下角的坐标确定，因此，可以循环遍历，从（0，0）开始遍历

   左上角   右下角

（0，0）（0，0）

（0，0）（0，1）

（0，0）（0，2）

（0，0）（0，3）

（0，0）（0，4）

............

分别求出每一中情况的和，在求最大值。

我是用C++实现的：

代码是：

#include<iostream>
#include<algorithm>
#include<math.h>
#include<vector>
using namespace std;

int n, m;
/*
struct cell {

int sum;
int num[2][2];

}cell[10010];
*/
void DoMax(int num[][100], int n, int m);//主要操作函数

int Mysum(int num[][100], int x, int y);//用于求出子矩阵的和

vector<int> MAX;

int main() {

cin >> n >> m;
int num[20][100];
for (int i = 0; i < n; i++) {

for (int j = 0; j < m; j++) {

cin >> num[i][j];

}

}

DoMax(num, n, m);
//cout << result;

}

int Mysum(int num[][100], int x1, int y1, int x2, int y2) {

int sum = 0;

for (int i = x1; i <= x2; i++) {

for (int j = y1; j <= y2; j++) {

sum += num[i][j];

}

}

return sum;

}

void DoMax(int num[][100], int n, int m) {

int myMax = num[0][0];

for (int i = 0; i < n; i++) {

for (int j = 0; j < m; j++) {

for (int k = i; k < n; k++) {

for (int l = j; l < m; l++) {

int temp = Mysum(num, i, j, k, l);
myMax = max(myMax, temp);
cout << "(" << i << j << k << l << ")" << temp << endl;
MAX.push_back(temp);
}

}

}

}

//sort(MAX.begin(), MAX.end());

cout << myMax;

}

结果截图：

 

 

 

 

 

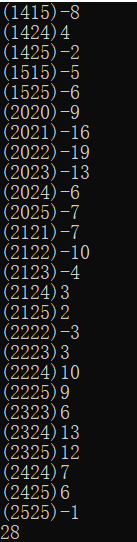
 在整个解题的过程中，我也想过很多办法，但是目前实现的就是这个方法，这个方法的时间复杂度还是很高的，在接下来的几天会继续优化。