输出激活函数与损失函数的理论知识

前文介绍

在深度学习中，输入值和矩阵的运算是线性的，而多个线性函数的组合仍然是线性函数，对于多个隐藏层的神经网络，如果每一层都是线性函数，那么这些层在做的就只是进行线性计算，最终效果和一个隐藏层相当！那这样的模型的表达能力就非常有限 。

实际上大多数情况下输入数据和输出数据的关系都是非线性的。所以我们通常会用非线性函数对每一层进行激活，大大增加模型可以表达的内容（模型的表达效率和层数有关）。这里通俗讲一下就是说：用激活函数可以更形象的表达他们之间的关系

这时就需要在每一层的后面加上激活函数，为模型提供非线性，使得模型可以表达的形式更多，同时也可以更改模型的输出值，使模型可以实现回归或者分类的功能。这里我们只介绍激活函数sigmoid、softmax。

一、sigmoid函数

　　输入值与权重矩阵进行计算得到的输出值范围很大，为了实现分类任务，需要使用激活函数sigmoid 把这些值压缩到0-1之间，表示某个分类的概率，通常用于二分类。sigmoid 的函数表达式如下：

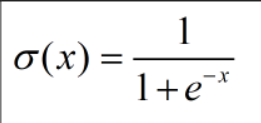
 对应的曲线：

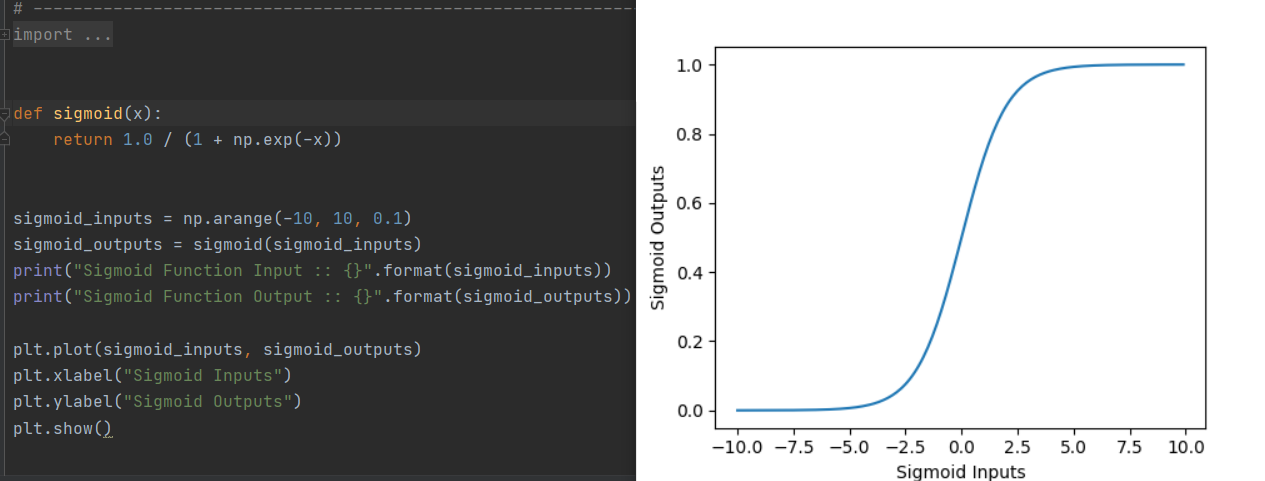
二、softmax函数 

在二分类任务中，输出层使用的激活函数为 sigmoid，而对于多分类的情况，就需要用到softmax 激活函数给每个类都分配一个概率。

多分类的情况下，神经网络的输出是一个长度为类别数量的向量，比如输出是(1,1,2)，为了计算概率，可以将其中的每个除以三者之和，得到 (0.25, 0.25, 0.5)。

但是这样存在一个问题，比如像 (1,1,-2) 这种存在负数的情况，这种方法就不行了。解决办法是先对每个元素进行指数操作，全部转换为正数，然后再用刚才的方法得到每个类别的概率。

softmax 函数将每个单元的输出压缩到 0 和 1 之间，是标准化输出，输出之和等于 1。softmax 函数的输出等于分类概率分布，显示了任何类别为真的概率。softmax 公式如下：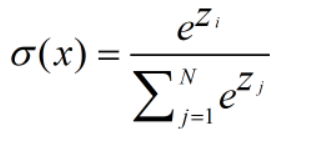

图像为：

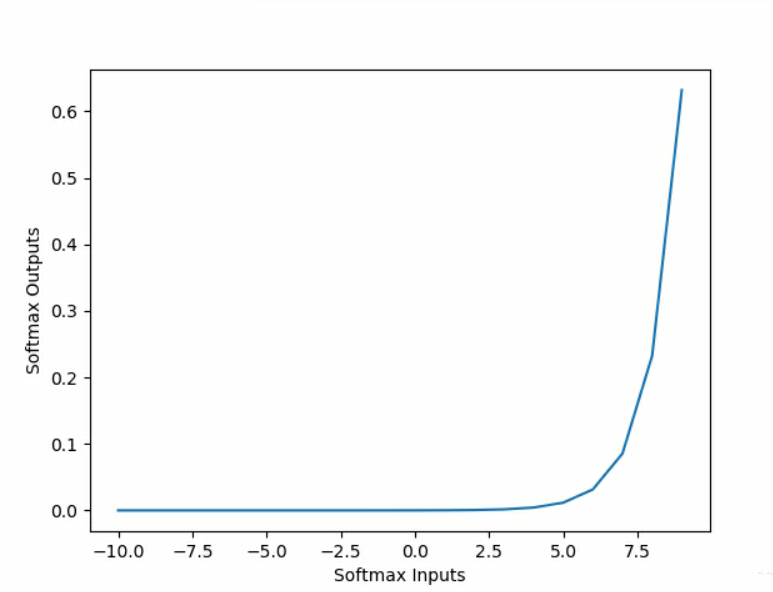
用更形象的例子表示为下图：

 

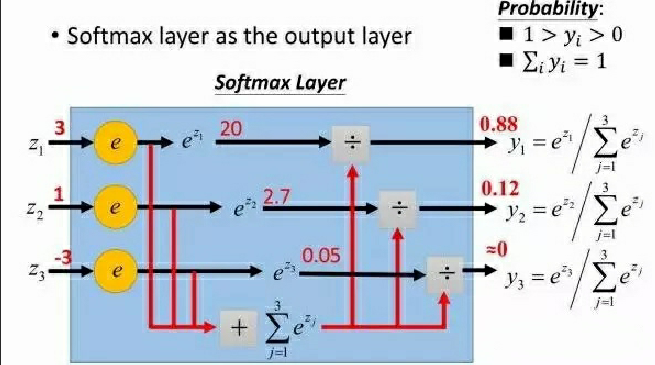
• softmax求导（详情请见此页）

三、损失函数

• 似然函数

　　对于这个函数：  输入有两个：x表示某一个具体的数据；  表示模型的参数

如果  是已知确定的，  是变量，这个函数叫做概率函数(probability function)，它描述对于不同的样本点  ，其出现概率是多少。

如果  是已知确定的，  是变量，这个函数叫做似然函数(likelihood function), 它描述对于不同的模型参数，出现  这个样本点的概率是多少。

这有点像“一菜两吃”的意思。其实这样的形式我们以前也不是没遇到过。例如，  , 即x的y次方。如果x是已知确定的(例如x=2)，这就是  , 这是指数函数。 如果y是已知确定的(例如y=2)，这就是  ，这是二次函数。同一个数学形式，从不同的变量角度观察，可以有不同的名字。

• 对数损失函数

　　对数损失函数的基本思想是极大似然估计，极大似然估计简单来说，就是一个事件已经发生了，那么就认为这事件发生的概率应该是最大的。似然函数就是这个概率，我们要做的就是基于现有数据确定参数从而最大化似然函数。

 　　在进行似然函数最大化时，会对多个事件的概率进行连续乘法。连续乘法中很多个小数相乘的结果非常接近0，而且任意数字发生变化，对最终结果的影响都很大。为了避免这两种情况，可以使用对数转换将连续乘法转换为连续加法。对数函数是单调递增函数，转换后不会改变似然函数最优值的位置。

 　　再加个负号，从而可以将求解最大似然函数转换为求解最小损失函数。二分类问题的对数损失函数如下：、

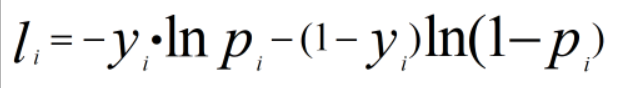
第一项表示预测正样本得到的损失，第二项表示预测负样本得到的损失。

其中 y表示实际情况下事件是否发生（0或1），p表示事件发生的概率，也就是我们通过深度学习得到的预测概率。

对于单个数据样本，会有如下两种情况（二分类中由sigmoid函数得到概率p）：

• 当y=1时，损失函数为 -ln(p)，如果想要损失函数尽可能的小，那么概率p就要尽可能接近1。
• 当y=0时，损失函数为 -ln(1-p)，如果想要损失函数尽可能的小，那么概率p就要尽可能接近0。

上面只是单个事件对应的损失，如果有m个独立事件，则损失函数公式如下：

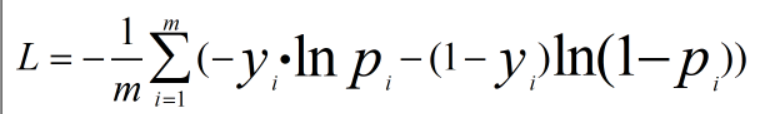
 通过一个例子来理解上面的公式。假设有三个独立事件，1表示事件发生，现在三个事件发生情况为(1,1,0)，通过深度学习得到三个事件发生的概率为(0.8, 0.7, 0.1)，使用上面的公式计算损失值为0.69，损失值很小，说明这组概率正确的可能性很大；同样的这组概率，三个事件发生情况为(0,0,1)，计算得到的损失值5.12，损失值很大，说明这组概率正确的可能性很小。

• 交叉熵损失函数

　　 上面的对数损失函数是针对二分类的，对于多分类问题，需要使用交叉熵损失函数，对数损失函数也被称为二分类的交叉熵损失函数。多类别中每个类别都对应一个概率，所以k个类别的交叉熵损失函数公式如下：

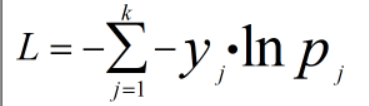
　　多分类中每个类的概率就需要用 softmax激活函数得到，而二分类中的概率是用sigmoid激活函数得到的。现在得到了多分类的损失函数，接下来就可以使用梯度下降算法来优化网络参数使得损失函数最小化。这里引用地址

　　其中sigmoid函数和softmax函数都是计算概率P的将其压缩在一定的范围值内；下面用一个例子来说明：

　　假设一个动物照片的数据集中有5种动物，且每张照片中只有一只动物，每张照片的标签都是one-hot编码。：只有一位为1其他都为0的独立站位；

　　第一张照片是狗的概率为100%，是其他的动物的概率是0；第二张照片是狐狸的概率是100%，是其他动物的概率是0，其余照片同理；因此可以计算下，每张照片的熵都为0。换句话说，以one-hot编码作为标签的每张照片都有100%的确定度，不像别的描述概率的方式：狗的概率为90%，猫的概率为10%。

　　假设有两个机器学习模型对第一张照片分别作出了预测：Q1和Q2,而第一张照片的真实标签为[1,0,0,0,0]。这里的真实标签其实就是“Y”；

两个模型预测效果如何呢，可以分别计算下交叉熵：

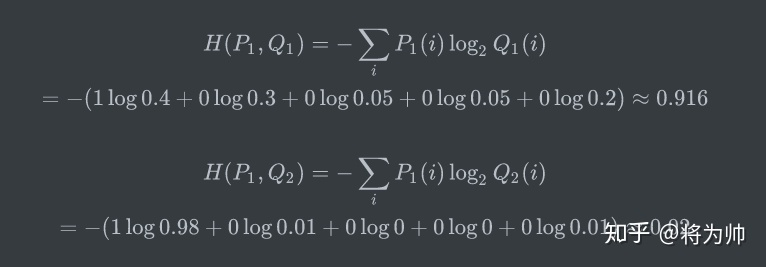交叉熵对比了模型的预测结果和数据的真实标签，随着预测越来越准确，交叉熵的值越来越小，如果预测完全正确，交叉熵的值就为0。因此，训练分类模型时，可以使用交叉熵作为损失函数。

注意！！：这里面的log本文都以e为底的对数

• 二分类交叉熵函数（其实就是上面的对数损失函数）

 　　其中P(cat)=1-P(dog)也可以表示为：

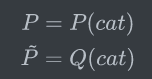
 二分类的交叉熵可以写作如下形式，看起来就熟悉多了。

 四、代码实现交叉熵函数

• soft函数的代码理解

 　　　　假设拥有三个输出节点的输出值为  为[2, 3, 5]。首先尝试不使用指数函数  ，接下来使用指数函数的（本知识链接）

Softmax函数计算。

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　#这里使用TensorFlow深度学习框架

import tensorflow as tf     　　　　　　　　　　　　

print(tf.__version__) # 2.0.0
a = tf.constant([2, 3, 5], dtype = tf.float32)
b1 = a / tf.reduce_sum(a) # 不使用指数----reduce_sum计算2+3+5=10
print(b1) # tf.Tensor([0.2 0.3 0.5], shape=(3,), dtype=float32)

b2 = tf.nn.softmax(a) # 使用指数的Softmax  这里就是运用上面softmax的公式计算的了
print(b2) # tf.Tensor([0.04201007 0.11419519 0.8437947 ], shape=(3,), dtype=float32)

　　结果还是挺明显的，经过使用指数形式的Softmax函数能够将差距大的数值距离拉的更大。

　 优点：在深度学习中通常使用反向传播求解梯度进而使用梯度下降进行参数更新的过程，而指数函数在求导的时候比较方便。比如  （详情请看链接内部）

下面来演示softmax函数计算P，然后用交叉熵损失函数

　　TensorFlow提供的统一函数式接口为：

import tensorflow as tf

print(tf.__version__) # 2.0.0
tf.keras.losses.categorical_crossentropy(y_true, y_pred, from_logits = False)

其中y_true代表了One-hot编码后的真实标签，y_pred表示网络的实际预测值：

• 当from_logits设置为True时，y_pred表示未经Softmax函数的输出值；
• 当from_logits设置为False时，y_pred表示为经过Softmax函数后的输出值；

为了在计算Softmax函数时候数值的稳定，一般将from_logits设置为True，此时tf.keras.losses.categorical_crossentropy将在内部进行Softmax的计算，所以在不需要在输出节点上添加Softmax激活函数。代码如下：

1、　　import tensorflow as tf
2、
3、　　print(tf.__version__)
4、　　z = tf.random.normal([2, 4]) # 构造2个样本的4类别输出的输出值
5、　　y = tf.constant([1, 3]) # 两个样本的真是样本标签是1和3
6、　　y_true = tf.one_hot(y, depth = 4) # 构造onehot编码
7、　　print（z）
8、　　# 输出层未经过Softmax激活函数,因此讲from_logits设置为True
9、　　loss1 = tf.keras.losses.categorical_crossentropy(y_true, z, from_logits = True)
10、　　loss1 = tf.reduce_mean(loss1)
11、　　print(loss1) 
12、　　
13、　　y_pred = tf.nn.softmax(z) 
14、　　print（y_pred）　# 输出层经过Softmax激活函数,因此讲from_logits设置为True
15、　　loss2 = tf.keras.losses.categorical_crossentropy(y_true, y_pred, from_logits = False)
16、　　loss2 = tf.reduce_mean(loss2)
17、　　print(loss2) 

这里为了方便讲解其中的代码函数什么意思我特意加了行号，这里只讲解难理解的一些代码行：

第4行是随机产生4个数值的2个样本预测值这里指的是公式中的P其实就是概率

第5行是2个样本的真实的标签也就是公式中的Y但是本代码运用了one-hot编码编码为第6行的输出值tf.Tensor([[0. 1. 0. 0.]，[0. 0. 0. 1.]], shape=(2, 4), dtype=float32)

第6行depth：其实就是输出的位数这里是4就是 [0.1.0.0]这个

第9行其实就是计算这个交叉熵函数了，这里将from_logits设置为True，此时tf.keras.losses.categorical_crossentropy将在内部进行Softmax的计算；内部的计算log是以e为底的对数这里我的输出值为：tf.Tensor(1.2350414, shape=(), dtype=float32)；这是这两个样本点的均值；具体计算由from_logits为Flase时解释；

第13行我们需要进行softmax函数将其概率P压缩到[0-1];这里就是因为第15行设为了Flase

由于第7行输出的一开始的随机值为①；经过softmax函数之后值变为了②（此时都变成了[0-1区间的随机概率了]）　

　　tf.Tensor(
　　[[-0.81390625  1.5490774  -0.4153358  -0.209876  ]
　　[-0.05958632 -0.28316626 -0.24799897 -1.0956372 ]], shape=(2, 4), dtype=float32)
②
　　tf.Tensor(
　　[[0.06692647 0.7109331  0.09969995 0.12244047]
　　[0.33525804 0.2680894  0.2776851  0.11896741]], shape=(2, 4), dtype=float32)

这里先写一下标签真实的one-hot编码　　tf.Tensor([[0. 1. 0. 0.]，[0. 0. 0. 1.]], shape=(2, 4), dtype=float32)

最后一步讲解15行的运算：

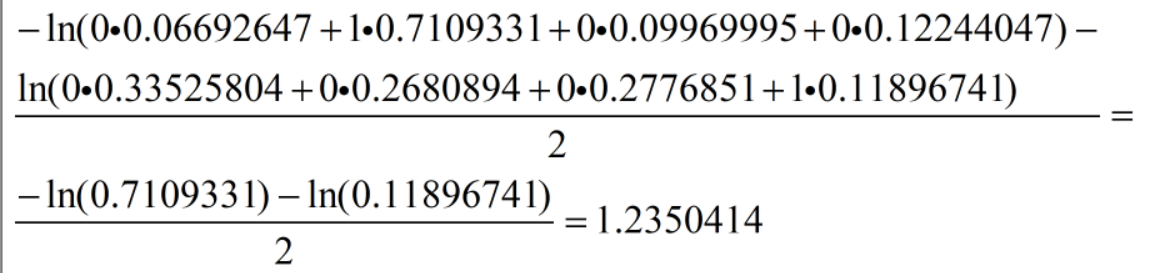
所以最后第17行输出的为：

tf.Tensor(1.2350414, shape=(), dtype=float32)