实验3 函数应用编程

实验1

#define _CRT_SECURE_NO_WARNINGS
#include<stdio.h>
#include<stdlib.h>

#include <stdio.h>
#include <stdlib.h>
#include <time.h>
#include <windows.h>
#define N 80
void print_text(int line, int col, char text[]); // 函数声明
void print_spaces(int n); // 函数声明
void print_blank_lines(int n); // 函数声明
int main() {
int line, col, i;
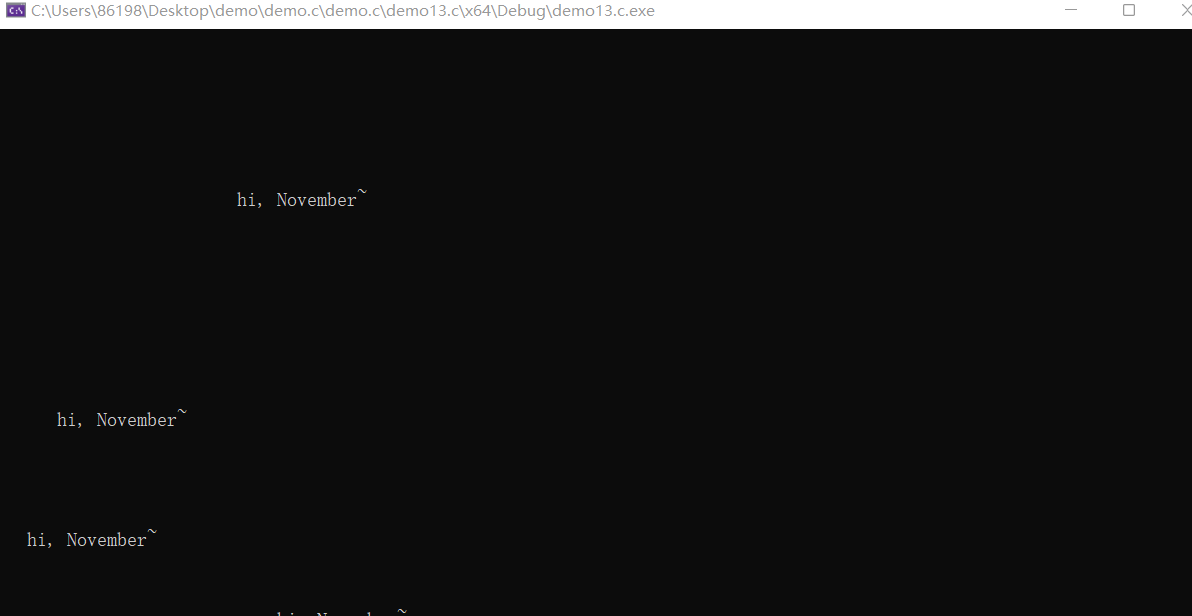
char text[N] = "hi, November~";
srand(time(0)); // 以当前系统时间作为随机种子
for (i = 1; i <= 10; ++i) {
line = rand() % 25;
col = rand() % 80;
print_text(line, col, text);
Sleep(1000); // 暂停1000ms
}
return 0;
}
// 打印n个空格
void print_spaces(int n) {


int i;
for (i = 1; i <= n; ++i)
printf(" ");
}
// 打印n行空白行
void print_blank_lines(int n) {
int i;
for (i = 1; i <= n; ++i)
printf("\n");
}
// 在第line行第col列打印一段文本
void print_text(int line, int col, char text[]) {
print_blank_lines(line - 1); // 打印(line-1)行空行
print_spaces(col - 1); // 打印(col-1)列空格
printf("%s", text); // 在第line行、col列输出text中字符串
}

 

 

 

 

 

 

实验2

task2.1

#define _CRT_SECURE_NO_WARNINGS

// 利用局部static变量的特性，计算阶乘
#include <stdio.h>
long long fac(int n); // 函数声明
int main() {
int i, n;
printf("Enter n: ");
scanf("%d", &n);
for (i = 1; i <= n; ++i)
printf("%d! = %lld\n", i, fac(i));
return 0;
}

// 函数定义
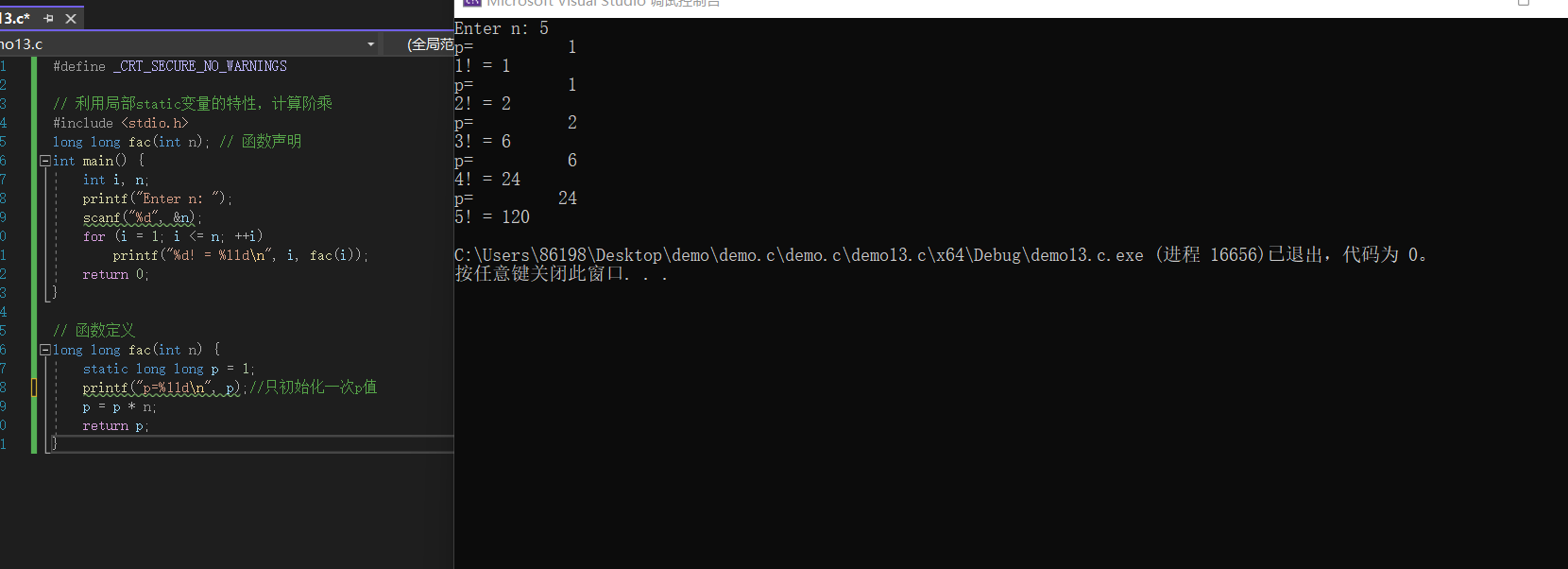
long long fac(int n) {
static long long p = 1; //只初始化一次p的值

printf("p=%11d\n", p);
p = p * n;
return p;
}

 

 

 

task2.2

#define _CRT_SECURE_NO_WARNINGS

// 练习：局部static变量特性
#include <stdio.h>
int func(int, int); // 函数声明
int main() {
int k = 4, m = 1, p1, p2;
p1 = func(k, m); // 函数调用
p2 = func(k, m); // 函数调用
printf("%d, %d\n", p1, p2);
return 0;
}
// 函数定义
int func(int a, int b) {
static int m = 0, i = 2;
i += m + 1;
m = i + a + b;
return m;
}

 

 

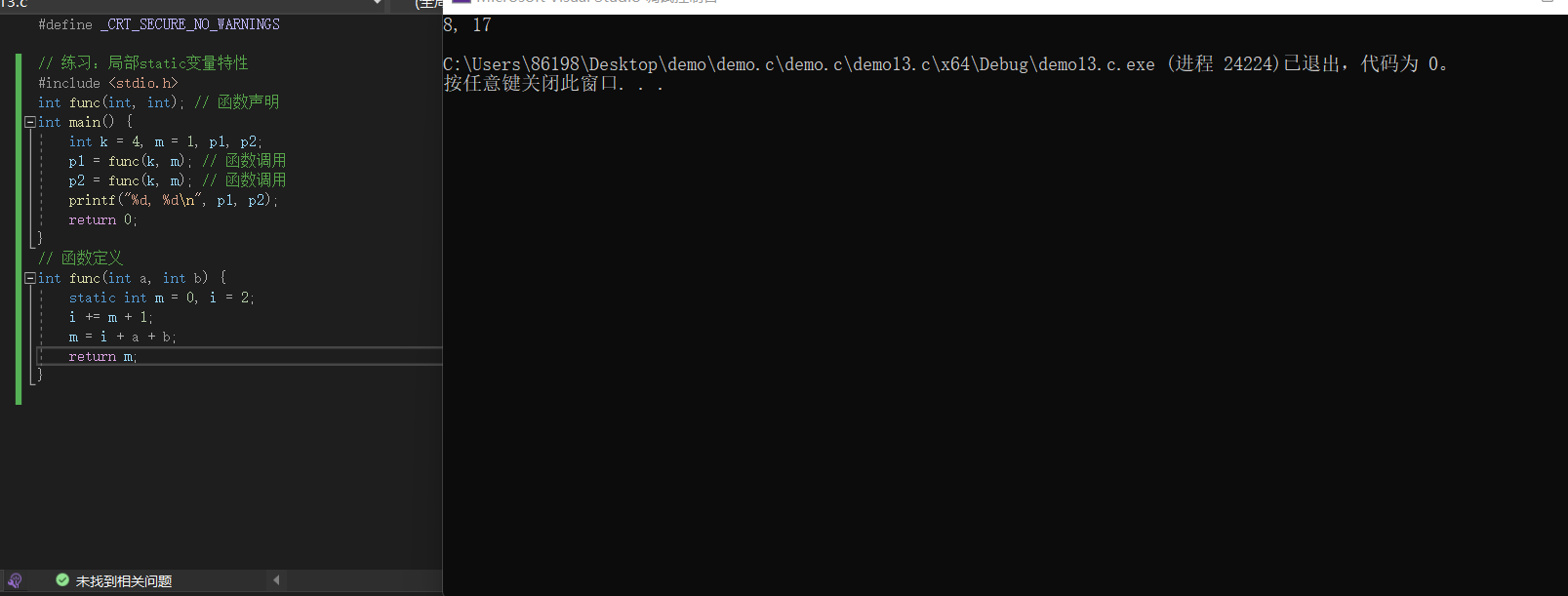
 局部static在局部起作用且只初始化变量一次

 

实验3

 

 

 

 

#define _CRT_SECURE_NO_WARNINGS

//已知数学函数式如下：（设n取值在0~32之间）
//设计一个函数模块func()，用来实现：提供n的数值，返回该函数计算式的结果。
//要求：
//使用递归算法实现
//不使用标准库函数pow()

#include <stdio.h>
long long func(int n); // 函数声明
int main() {
int n;
long long f;
while (scanf("%d", &n) != EOF) {
f = func(n); // 函数调用
printf("n = %d, f = %lld\n", n, f);
}
return 0;
}
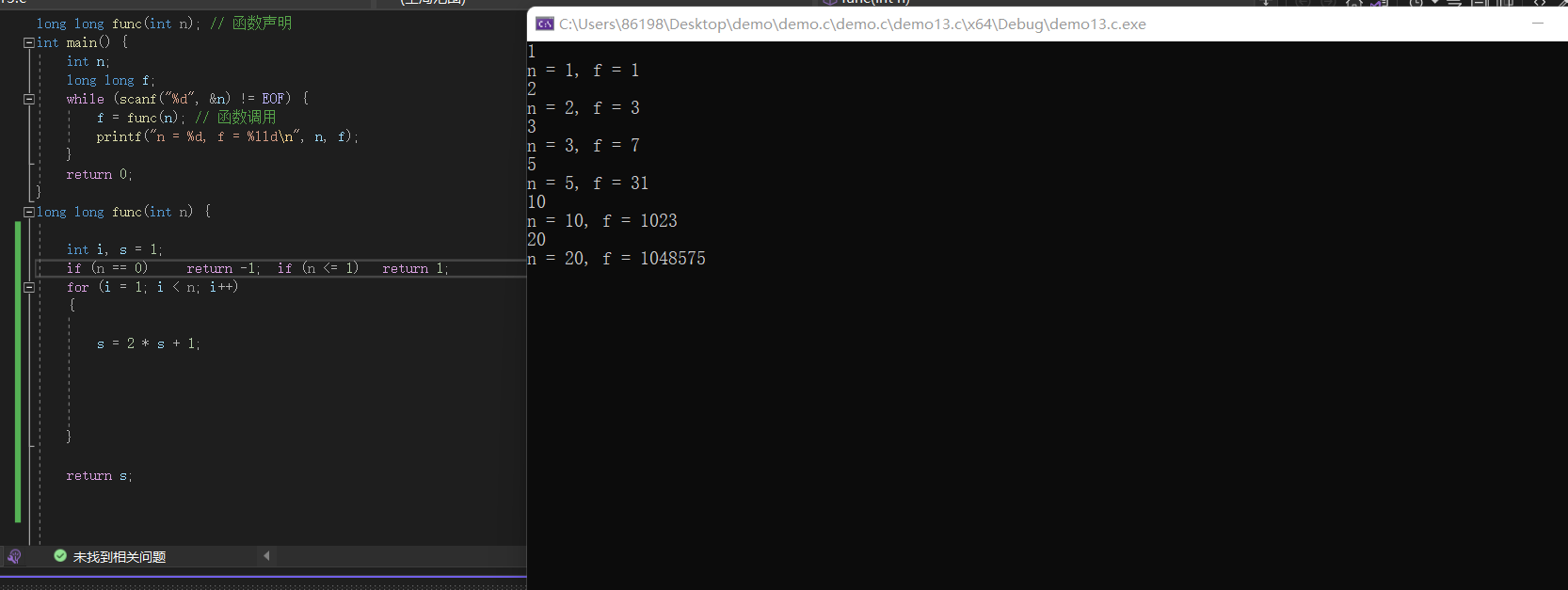
long long func(int n) {

int i, s = 1;
if (n == 0) return -1; if (n <= 1) return 1;
for (i = 1; i < n; i++)
{

s = 2 * s + 1;

 

}

return s;

}

 

 

 

实验4

 

#include<stdio.h>
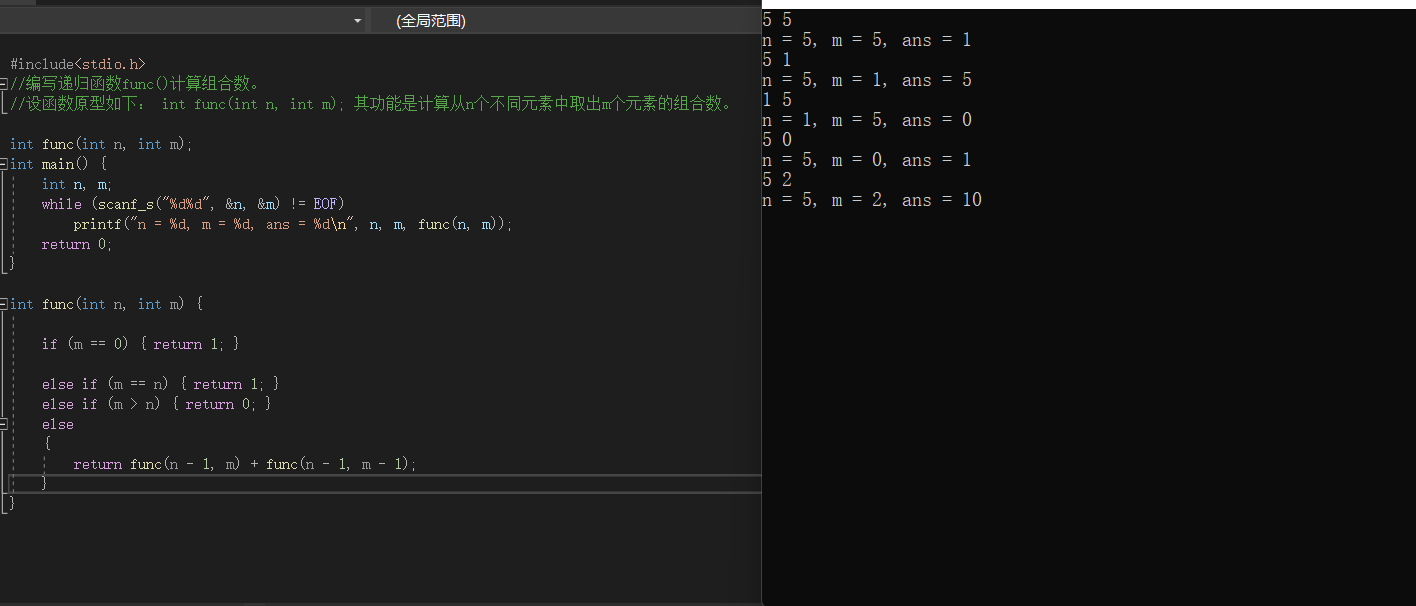
//编写递归函数func()计算组合数。
//设函数原型如下： int func(int n, int m); 其功能是计算从n个不同元素中取出m个元素的组合数。

int func(int n, int m);
int main() {
int n, m;
while (scanf_s("%d%d", &n, &m) != EOF)
printf("n = %d, m = %d, ans = %d\n", n, m, func(n, m));
return 0;
}

int func(int n, int m) {

if (m == 0) { return 1; }

else if (m == n) { return 1; }
else if (m > n) { return 0; }
else
{
return func(n - 1, m) + func(n - 1, m - 1);
}
}

 

 

实验5

#define _CRT_SECURE_NO_WARNINGS
#include<stdio.h>
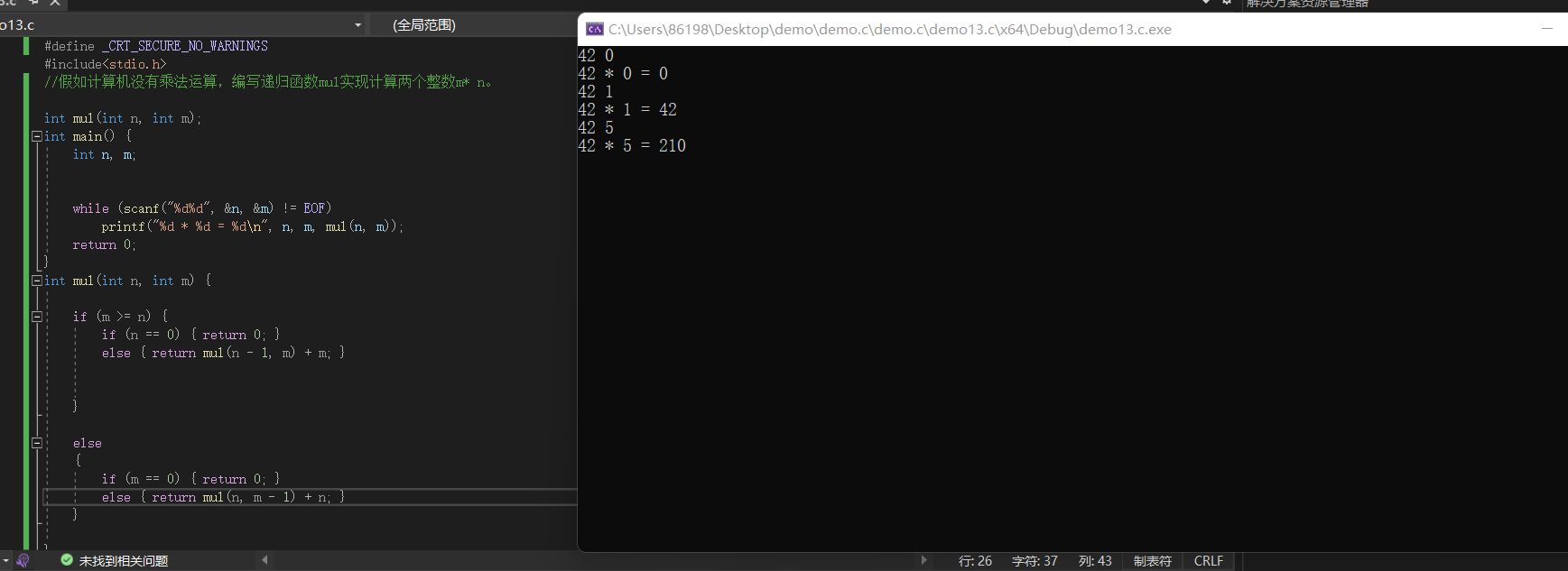
//假如计算机没有乘法运算，编写递归函数mul实现计算两个整数m* n。

int mul(int n, int m);
int main() {
int n, m;

while (scanf("%d%d", &n, &m) != EOF)
printf("%d * %d = %d\n", n, m, mul(n, m));
return 0;
}
int mul(int n, int m) {

if (m >= n) {
if (n == 0) { return 0; }
else { return mul(n - 1, m) + m; }

}

else
{
if (m == 0) { return 0; }
else { return mul(n, m - 1) + n; }
}

}

 

 

实验6

 

#define _CRT_SECURE_NO_WARNINGS
#include<stdio.h>
void moveplate(unsigned int n, char from, char to);
void hanoi(unsigned int n, char from, char temp, char to);
int count = 0;
int main()
{
unsigned int n;
printf("请输入你需要进行移动的盘子数：\n");
while (scanf_s("%d", &n) != EOF)
{
count = 0;
printf("请输入你需要进行移动的盘子数：\n");
hanoi(n, 'A', 'B', 'C');
printf("移动盘子的总次数为：%d\n", count);
}

 

return 0;

 

}
void moveplate(unsigned int n, char from, char to)
{
printf("%u:%c-->%c\n", n, from, to);
count++;
}
void hanoi(unsigned int n, char from, char temp, char to)
{
if (n == 1)
moveplate(n, from, to);
else
{
hanoi(n - 1, from, to, temp);
moveplate(n, from, to);
hanoi(n - 1, temp, from, to);
}
}

 

 

实验7

 

#define _CRT_SECURE_NO_WARNINGS
#include<stdio.h>
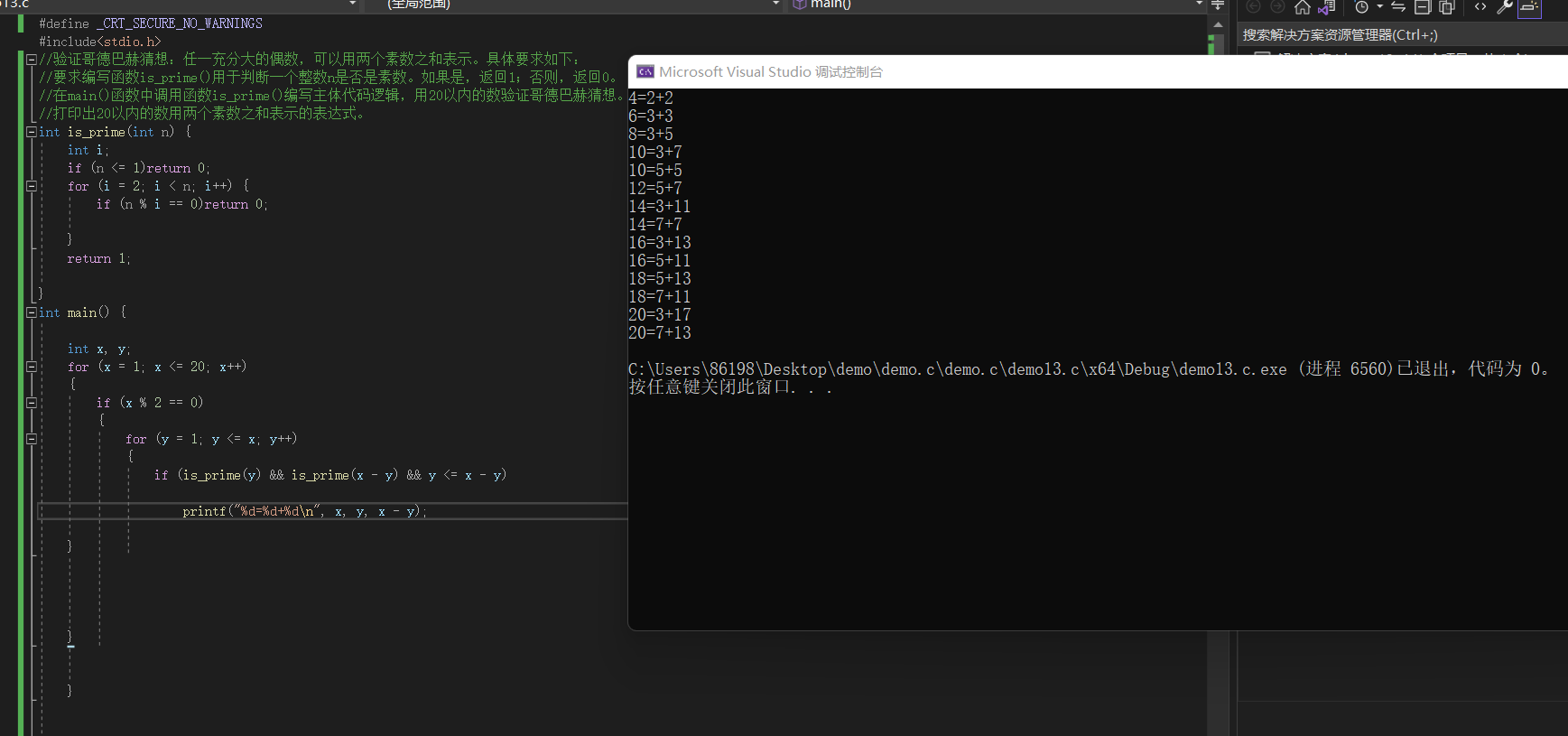
//验证哥德巴赫猜想：任一充分大的偶数，可以用两个素数之和表示。具体要求如下：
//要求编写函数is_prime()用于判断一个整数n是否是素数。如果是，返回1；否则，返回0。
//在main()函数中调用函数is_prime()编写主体代码逻辑，用20以内的数验证哥德巴赫猜想。
//打印出20以内的数用两个素数之和表示的表达式。
int is_prime(int n) {
int i;
if (n <= 1)return 0;
for (i = 2; i < n; i++) {
if (n % i == 0)return 0;

}
return 1;

}
int main() {

int x, y;
for (x = 1; x <= 20; x++)
{
if (x % 2 == 0)
{
for (y = 1; y <= x; y++)
{
if (is_prime(y) && is_prime(x - y) && y <= x - y)

printf("%d=%d+%d\n", x, y, x - y);
}
}

}
}

 

 

实验8

 

#define _CRT_SECURE_NO_WARNINGS
#include<stdio.h>
//编写函数func，实现将一个长整型数s的每一数位上的奇数依次取出来，构成一个新的数，高位仍在高
//位，低位仍在低位，返回这个新数。例如，s = 20211124时，调用函数fun后，返回111。
//在主函数中，通过多组输入方式，多次调用fun()，实现对多组数据的测试
long fun(long s); // 函数声明
int main() {
long s, t;
printf("Enter a number: ");
while (scanf("%ld", &s) != EOF) {
t = fun(s); // 函数调用
printf("new number is: %ld\n\n", t);
printf("Enter a number: ");
}
return 0;
}
long fun(long s) {
int i, j, m, n; int num[100];
i = 0; j = s; n = 0;
while (j != 0)
{
if (j % 2 == 1)
{

num[i] = j % 10; i++;

 

}
j = j / 10;
}
for (m = i-1; m >= 0; m--)
{
n = n * 10 + num[m];
}return n;

 

}