Python机器学习笔记：主成分分析（PCA）算法

完整代码及其数据，请移步小编的GitHub

　　传送门：请点击我

　　如果点击有误：https://github.com/LeBron-Jian/MachineLearningNote

一：引入问题

　　首先看一个表格，下表是某些学生的语文，数学，物理，化学成绩统计：

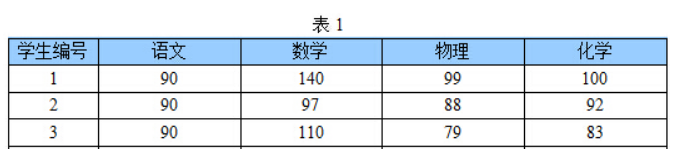
　　首先，假设这些科目成绩不相关，也就是说某一科目考多少分与其他科目没有关系，那么如何判断三个学生的优秀程度呢？首先我们一眼就能看出来，数学，物理，化学这三门课的成绩构成了这组数据的主成分（很显然，数学作为第一主成分，因为数据成绩拉的最开）。

　　那么为什么我们能一眼看出来呢？

　　当然是我们的坐标轴选对了！！

　　下面，我们继续看一个表格，下标是一组学生的数学，物理，化学，语文，历史，英语成绩统计：

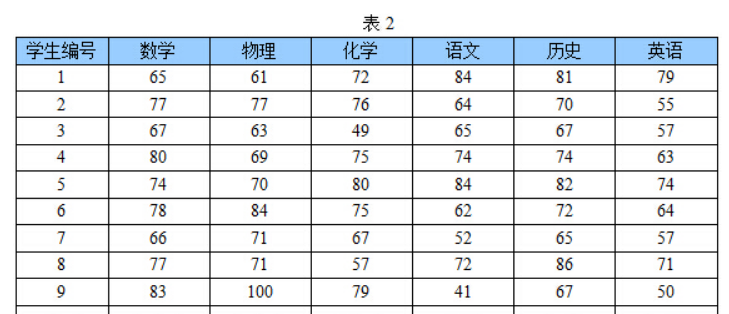
　　那么这个表我们能一眼看出来吗？

　　数据太多了，以至于看起来有些凌乱，无法直接看出这组数据的主成分，因为在坐标系下这组数据分布的很散乱。究其原因，是因为无法拨开遮住肉眼的迷雾，如果把这些数据在相应的空间中表示出来，也许你就能换一个观察角度找出主成分，如下图所示：

　　简单的二维或者三维我们可以想象出来其分布状态，那么对于更高维的数据，能想象出来其分布吗？还有，就算能描述分布，如何精确地找到这些主成分的轴？如何衡量你提取的主成分到底占了整个数据的多少信息？所以，我们就要用到主成分分析的处理方法。

　　为了说明什么是数据的主成分，我们首先得了解数据降维，数据降维时怎么回事？

二，数据降维

　　假设三维空间中有一系列点，这些点分布在一个过原点的斜面上，如果你用自然坐标x,y,z这三个轴来表示这组数据的话，需要使用三个维度，而事实上，这些点的分布仅仅是在一个二维的平面上，那么问题出在哪里？如果你仔细想想，能不能把x,y,z坐标系旋转一下，使数据所在平面与x，y平面重合？这就对了！如果把旋转后的坐标记为x'，y'，z'，那么这组数据的表示只用x'和y'两个维度表示即可！

　　当然了，如果想恢复原来的表示方式，那就得把这两个坐标之间的变换矩阵存下来。这样就能把数据维度降下来了！但是，我们要看到这个过程的本质，如果把这些数据按行或者按类排成一个矩阵，那么这个矩阵的秩就是2！这些数据之间是有相关性的，这些数据构成的过原点的向量的最大线性无关组包含2个向量，这就是为什么一开始就假设平面过原点的原因！

　　那么如果不过原点呢？这就是数据中心化的缘故！将坐标原点平移到数据中心，这样原本不相关的数据在这个新坐标系中就有相关性了！有趣的是，三点一定共面，也就是三维空间中任意三点中心化后都是线性相关的，一般来讲n维空间中n个点一定能在一个n-1维子空间中分析！

　　总结一下这个例子，数据降维后并没有丢弃任何东西，因为这些数据在平面以外的第三个维度的分量都为0。现在，假设这些数据在z'轴有一个很小的抖动，那么我们仍然用上述的二维表示这些数据，理由是我们可以认为这两个轴的信息是数据的主成分，而这些信息对于我们的分析已经足够了，z'轴上的抖动很有可能是噪音，也就是说本来这组数据是有相关性的，噪声的引入，导致了数据不完全相关，但是，这些数据在z'轴上的分布与原点构成的夹角非常小，也就是说在z'轴上有很大的相关性，综合考虑，就可以认为数据在x'，y'轴上的投影构成了数据的主成分！

　　所以说，降维肯定意味着信息的丢失，不过鉴于实际数据本身常常存在的相关性，我们可以想办法在降维的同时将信息的损失尽量降低。

　　下面在说一个极端的情况，也许在现实中不会出现，但是 类似的情况还是很常见的。

　　假设某学籍数据有两列M和F，其中M列的取值是如果此学生为男性，则取值为1，为女性则取0；而F列是学生为女性，则取值为0，男性则为1.此时如果我们统计全部学籍数据，会发现对于任何一条记录来说，当M为1时F必定为0，反之当M为0时F必定为1，在这种情况下，我们将M或者F去掉实际上没有任何信息的损失，因为只要保留一列就可以完全还原另一列。

　　那么降维我们差不多说清楚了，现在我们将自己面对的数据抽象为一组向量，那么下面我们有必要研究一些向量的数学性质，而这些数学性质将成为后续推导出PCA的理论基础。

 三，PCA基本数学原理

3.1 内积与投影

　　下面先看一个向量运算：内积。

　　两个维数相同的向量的内积被定义为：

　　内积运算将两个向量映射为一个实数，其计算方式非常容易理解，但是其意义并不明显，下面我们分析内积的几何意义。假设A和B是两个n维向量，我们知道n维向量可以等价表示为n维空间中的一条从原点发射的有向线段，为了简单起见，我们假设A和B均为二维向量，则

　　那么在二维平面上A和B可以用两条发自原点的有向线段表示，如下图：

　　现在我们从A点向B所在直线引入一条垂线，我们知道垂线与B的交点叫做A在B上的投影，再假设A与B的夹角为a，则投影的矢量长度为（这里假设向量B的模为1）

　　其中是向量A的模，也就是A线段的标量长度。

　　注意这里区分了矢量长度和标量长度，标量长度总是大于等于0，值就是线段的长度；而矢量长度可能为负，其绝对值是线性长度，而符号取决于其方向与标准方向相同或者相反。

　　可能大家还没明白内积和这个东西有什么关系，不过我们将内积表示为另一种我们熟悉的方式：

　　现在明白了点吧，A与B的内积等于A到B的投影长度乘以B的模，在进一步，如果我们假设B的模为1，即让，那么就变成了下面公式（也就是上面我们说的投影的矢量长度）：

　　也就是说，设向量B的模为1，则A与B的内积值等于A向B所在直线投影的矢量长度！这就是内积的一种几何解释，也就是我们得到的第一个重要结论。

3.2 基

　　下面我们继续在二维空间讨论向量，上文说过，一个二维向量可以对应二维笛卡尔直角坐标系中从原点出发的一条有向线段，例如下面这个向量：

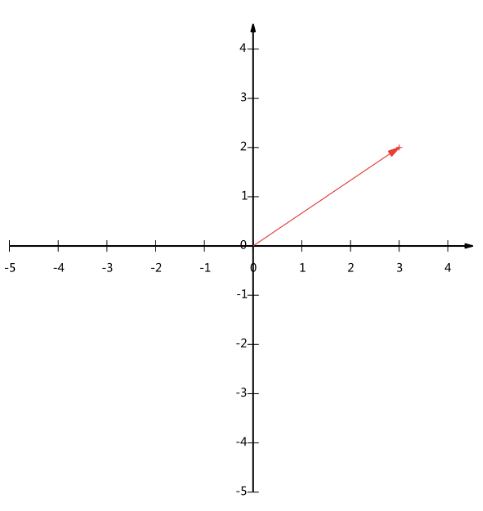
 　　在代数表示方面，我们经常使用线段终点的点的坐标表示向量，例如上面的向量可以表示为（3,2），这里我们再熟悉不过的向量表示。

　　不过我们常常忽略，只有一个（3,2）本身是不能够精确表示一个向量的，我们仔细看一下，这里的坐标（3,2）实际上表示的是向量在x轴上的投影值3，在y轴上的投影值为2。也就是说我们使其隐式引入一个定义：以x轴和y轴上正方向长度为1的向量为标准，那么一个向量（3,2）实际上是说在x轴投影为3而y轴投影为2.注意投影是一个矢量，所以可以为负。

　　更正式的说，向量（x,y）实际上表示线性组合：

　　不难证明所有二维向量都可以表示为这样的线性组合，此处（1,0）和（0，1）叫做二维空间的一组基。

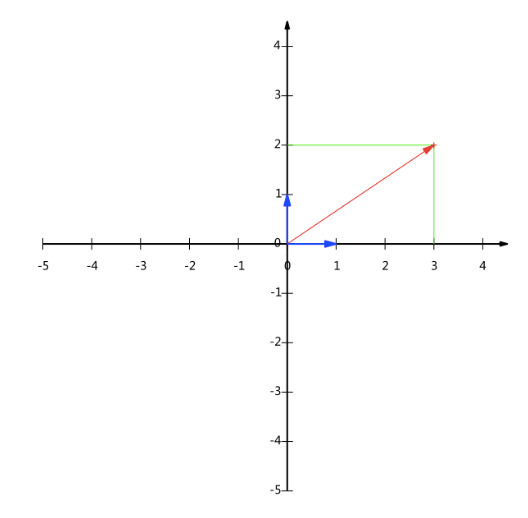
　　所以，要准确描述向量，首先要确定一组基，然后给出基所在的各个直线上的投影值，就可以了，只不过我们经常省略第一步，而默认以（1,0）和（0,1）为基。

　　我们之所以默认选择（1,0）和（0,1）为基，当然是比较方便，因为他们分别是x和y轴正方向上的单位向量，因此就使得二维平面上点坐标和向量一一对应，非常方便。但实际上任何两个线性无关的二维向量都可以成为一组基，所谓线性无关在二维平面内可以直观认为是两个不再一条直线上的向量。

　　例如，（1，1）和（1，-1）也可以成为一组基。一般来说，我们希望基的模是1，因为从内积的意义可以看到，如果基的模式1，那么就可以方便的用向量点乘基而直接获得其在新基上的坐标了！实际上，对应于任何一个向量我们总可以找到其同方向上模为1的向量，只要让两个分量分别除以模就好了，例如上面的基就可以变为：(1/ √2,  1/ √2 ) 和 (-1/ √2,  1/ √2 )。

　　现在我们想获得（3,2）在新基上的坐标，即在两个方向上的投影矢量值，那么根据内积的几何意义，我们只要分别计算（3,2）和两个基的内积，不难得到新的坐标为(5/ √2,  -1/ √2 )。

　　下图给出了新的基以及（3,2）在新基上坐标值的示意图：

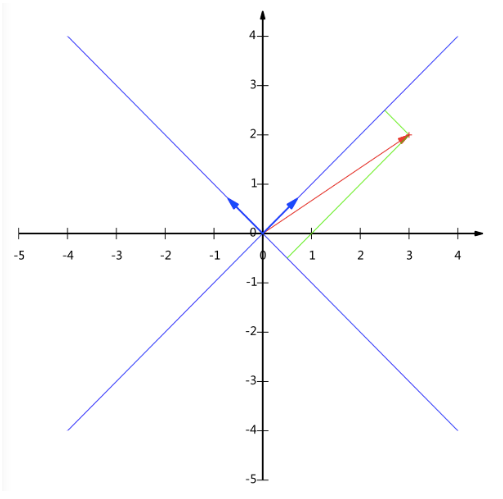
　　另外这里要注意的是，我们列举的例子中基是正交的（即内积为0，或者说相互垂直），但是可以成为一组基的唯一要求就是线性无关，非正交的基也是可以的，不过因为正交基有较好的性质，所以一般使用的基都是正交的。

3.3 基变换的矩阵表示

　　下面我们找一种简单的方式来表示基变换，还是拿上面的例子，想一下，将（3,2）变换为新基上的坐标，就是用（3,2）与第一个基做内积运算，作为第一个新的坐标分量，然后用（3,2）与第二个基做内积运算，作为第二个新坐标的分量。实际上，我们可以用矩阵想成的形式简洁的表示这个变换：

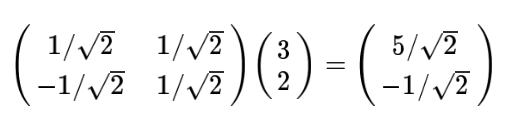
　　那么其中矩阵的两行分别为两个基，乘以原向量，其结果刚好为新基的坐标，可以稍微扩展一下，如果我们有m个二维向量，只要将二维向量按照列排成一个两行m列的矩阵，然后用“基矩阵”乘以这个矩阵，就得到了所有这些向量在新基下的值，例如（1,1），（2，2），（3,3）想变换到刚才那组基上，则可以变为这样：

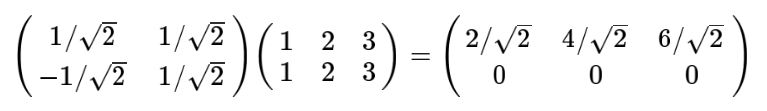
　　于是一组向量的基变换被表示为矩阵的相乘。

　　一般地，如果我们有M个N维向量，想将其变换为由R个N维向量表示的新空间中，那么首先将R个基按照行组成矩阵A,，然后将向量按照列组成矩阵B，那么两个矩阵的乘积AB就是变换结果，其中AB的第m列为A中的第M列变换后的结果。

　　数学表示为：

　　其中P_{i是一个行向量，表示第i个基，aj是一个列向量，表示第j个原始数据记录。}

　　特别要注意的是，这里R可以小于N，而R决定了变换后数据的维数，也就是说，我们可以将一个N维数据变换到更低维度的空间中去，变换后的维度取决于基的数量，因此这种矩阵相乘的表示也可以表示为降维变换。 

 　　最后，上述分析同时给矩阵相乘找到了一种物理解释：两个矩阵相乘的意义是将右边矩阵中每一列列向量变换到左边矩阵中每一行行向量为基所表示的空间中去。更抽象的说：一个矩阵可以表示为一种线性变换。

3.4 协方差矩阵及优化目标

　　上面我们讨论了选择不同的基可以对同样一组数据给出不同的表示，而且如果基的数量少于向量的本身的维数，则可以达到降维的效果，但是我们还没有回答最关键的一个问题：如何选择基才是最优的，或者说，如果我们有一组N维向量，现在要将其降到K维（K小于N），那么我们应该如何选择K个基才能最大程度保留原有的信息？

　　要完全数学化这个问题非常繁杂，这里我们用一个非形式化的直观方法来看这个问题。

　　为了避免过于抽象的讨论，我们仍然以一个具体的例子展开，假设我们的数据由五条记录组成，将它们表示为矩阵形式：

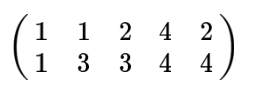
　　其中每一列为一条数据记录，而一行为一个字段，为了后续处理方便，我们首先将每个字段内所有值都减去字段均值，其结果是将每个字段都变为均值为0（这样做的好处后面可以看到）。

　　我们看上面的数据，第一个字段的均值为2，第二个字段的均值为3，所以变换后：

　　我们可以看到五条数据在平面直角坐标系内的样子：

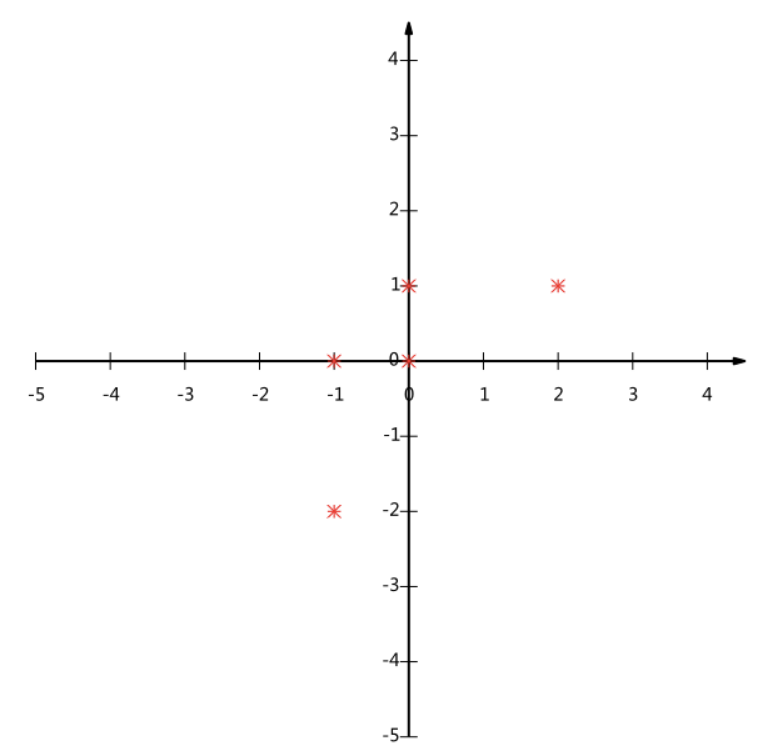
　　现在问题来了：如果我们必须使用一维来表示这些数据，又希望尽量保留原始的信息，你要如何选择？

　　通过上一节对及变换的讨论我们知道，这个问题实际上是要在二维平面中选择一个方向，将所有数据都投影到这个方向所在的直线上，用投影值表示原始记录，这是一个实际的二维降到一维的问题。

　　那么如何选择这个方向（或者说是基）才能尽量保留最多的原始信息呢？一种直观的看法是：希望投影后的投影值尽可能分散。

　　以上图为例，可以看出如果向x轴投影，那么最左边的两个点会重叠在一起，中间的两个点也会重叠在一起，于是本身四个各不相同的二维点投影后只剩下两个不同的值了，这是一种严重的信息丢失，同理，如果向y轴投影最上面的两个点和分布在x轴上的两个点也会重叠，所以看来x和y轴都不是最好的投影选择。我们直观目测，如果向通过第一象限和第三象限的斜线投影，则五个点在投影后还是可以区分的。

　　下面我们用数学方法表述这个问题。

3.5 方差

　　上文说道，我们希望投影后投影值尽可能分散，而这种分散程度，可以用数学上的方差来表述，此处，一个字段的方差可以看做事每个元素与字段均值的差的平方和的均值，即：

　　由于上面我们已经将每个字段的均值都化0 了，因此方差可以直接用每个元素的平方和除以元素个数表示：

　　于是上面的问题被形式化表示为：寻找一个一维基，使得所有数据变换为这个基上的坐标表示后，方差值最大。

3.6 协方差

　　对于上面二维降成一维的问题来说，找到那个使得方差最大的方向就可以了，不过对于更高维，还有一个问题需要解决，考虑三维降到二维问题，与之前相同，首先我们希望找到一个方向使得投影后方差最大，这样就完成了第一个方向的选择，继而我们选择第二个投影方向。

　　如果我们还是单纯的只选择方差最大的方向，很显然，这个方向与第一个方向应该是“几乎重合在一起”，显然这样的维度是没有用的，因此应该有其他约束条件。从直观上讲，让两个字段尽可能表示更多的原始信息，我们是不希望他们之间存在线性相关性，因为相关性意味着两个字段不是完全独立，必然存在重复表示的信息。

 　　数字上可以用两个字段的协方差表示其相关性，由于已经让每个字段均值为0，则：

　　可以看出，在字段均值为0的情况下，两个字段的协方差简洁的表示为其内积除以元素数m。

　　当协方差为0时，表示两个字段完全独立，为了让协方差为0，我们选择第二个即时只能在与第一个基正交的方向上选择。因此最终选择的两个方向一定是正交的。

　　至此，我们得到了降维问题的优化目标：将一组N维向量降维k维（K大于0，小于N），其目标是选择K个单位（模为1）正交基，使得原始数据变换到这组基上后，各字段两两间协方差为0，而字段的方差则尽可能大（在正交的约束下，取最大的k个方差）。

　　然后我们用X乘以X的转置，并乘上系数1/m：

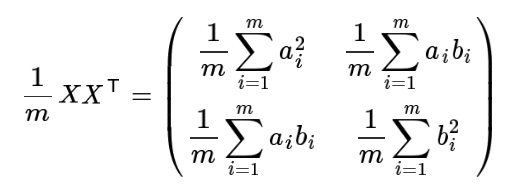
　　这时候我们会发现，这个矩阵对角线上的两个元素分别是两个字段的方差，而其他元素是a和b的协方差，两者被统一到了一个矩阵的。

　　根据矩阵相乘的运算法则，这个结论很容易被推广到一般情况：

　　设我们有m个n维数据记录，将其按列排成n乘m的矩阵X，设 C= 1/m*X*X^T ，则C是一个对称矩阵，其对角线分别是各个字段的方差，而第l行j列和j行i列元素相同，表示i和j两个字段的协方差。

3.7 协方差矩阵

　　上面我们导出了优化目标，但是这个目标似乎不能直接作为操作指南（或者说算法），因为它只说要什么，但是根本没有说怎么做，所以我们要在数学上继续研究计算方案。

　　我们看到，最终要达到的目标与字段内方差及字段间协方差有密切关系。因此我们希望能将两者统一表示，仔细观察发现，两者均可以表示为内积的形式，而内积又与矩阵相乘密切相关。于是，我们来了灵感：

　　假设我们只有a和b 两个字段，那么我们将他们按行组成矩阵X：

 

3.8 协方差矩阵对角化

　　根据上述推导，我们发现要达到优化目前等价于将协方差矩阵对角化：即除对角线外的其他元素化为0，并且在对角线上将元素按照大小从上到下排列，这样我们就达到了优化目的，这样说可能还不清晰，我们进一步看下原矩阵与基变换后矩阵协方差矩阵的关系：

　　设原始数据矩阵X对于的协方差矩阵为C，而P是一组基按行组成的矩阵，设Y=PX，则Y为X对P做基变换后的数据，设Y的协方差矩阵为D，我们推导一下D与C的关系：

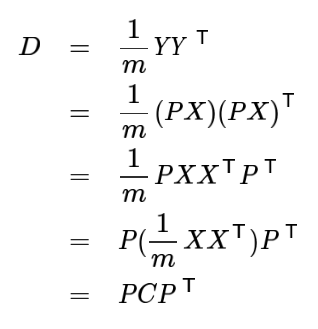
　　现在事情很明白，我们要找的P不是别的，而是能让原始协方差矩阵对角化的P，换句话说，优化目标变成了寻找一个矩阵P，满足PCP^T是一个对角矩阵，并且对角元素按照从大到小依次排列，那么P的前K行就是要寻找的基，用P的前K行就是要寻找的基，用P的前K行组成的矩阵乘以X就使得X从N维降到了K维并满足上述优化条件。

　　至此，我们离“发明”PCA还有一步之遥！

　　现在所有的焦点都聚集在了协方差矩阵对角化问题上，有时，我们真应该感谢数学家的先行，因为矩阵对角化在线性代数领域已经属于被玩烂的东西，所以这在数学上根本不是问题。

　　由上文知道，协方差矩阵C是一个对称矩阵，在线性代数上，实对称矩阵有一系列非常好的性质：

　　1）实对称矩阵不同特征值对应的特征向量必然正交。

　　2）设特征向量 λ 重数为r，则必然存在r个线性无关的特征向量对应于 λ，因此可以将这r个特征向量单位正交化。

　　有上面两条可知，一个n行n列的实对称矩阵一定可以找到n个单位正交特征向量，设这n个特征向量为e1, e2, ...en，我们将其按照列组成矩阵：

　　则对协方差矩阵C有如下结论：

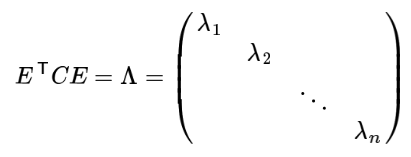
　　其中 Λ 为对称矩阵，其对角元素为各特征向量对应的特征值（可能有重复）。

　　到这里，我们发现我们已经找到了需要的矩阵P：

　　P是协方差矩阵的特征向量单位化后按照行排列出的矩阵，其中每一行都是C的一个特征向量，如果设P按照 Λ 中特征值从大到小，将特征向量从上到下排列，则用P的前K行组成的矩阵乘以原始数据矩阵X，就可以得到我们需要的降维后的数据矩阵Y。

　　至此，我们完成了整个PCA的数学原理讨论。

3.9 对上面例子整合

　　1，原始数据集矩阵X：

　　2，均值为（2， 3），求均值后：

　　3，再求协方差矩阵：

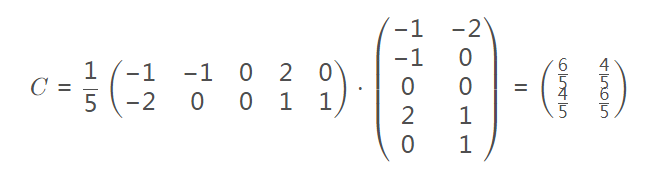
　　4，特征值：

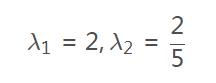
　　5，对应的特征向量：

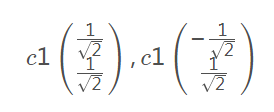
　　6，标准化：

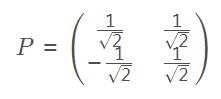
　　7，选择较大特征值对应的特征向量：

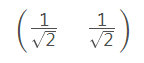
　　8，执行PCA变换：Y=PX 得到的Y就是PCA降维后的值 数据集矩阵：

　　9，计算代码：

from  numpy  import *

li = [[1,1],[1,3],[2,3],[4,4],[2,4]]
matrix = mat(li)
# 求均值
mean_matrix = mean(matrix,axis=0)
# print(mean_matrix.shape)
# 减去平均值
Dataadjust = matrix - mean_matrix
# print(Dataadjust.shape)
#计算特征值和特征向量
covMatrix = cov(Dataadjust,rowvar=0)
eigValues , eigVectors = linalg.eig(covMatrix)
# print(eigValues.shape)
# print(eigVectors.shape)
# 对特征值进行排序
eigValuesIndex = argsort(eigValues)
# print(eigValuesIndex)
# 保留前K个最大的特征值
eigValuesIndex = eigValuesIndex[:-(1000000):-1]
# print(eigValuesIndex)
# 计算出对应的特征向量
trueEigVectors = eigVectors[:,eigValuesIndex]
# print(trueEigVectors)
# 选择较大特征值对应的特征向量
maxvector_eigval = trueEigVectors[：，0]
# print(maxvector_eigval)
# 执行PCA变换：Y=PX 得到的Y就是PCA降维后的值 数据集矩阵
pca_result = maxvector_eigval * Dataadjust.T
print(pca_result)

　　

　　10，代码执行结果：

[[-2.12132034 -0.70710678  0.          2.12132034  0.70710678]]

　　

四，主成分分析（PCA）算法步骤

　　介绍一个PCA的教程：A tutorial on Principal Components Analysis ——Lindsay I Smith

 

　　PCA（Principal Components Analysis）即主成分分析，是一种常用的数据分析手段，是图像处理中经常用到的降维方法。对于一组不同维度之间可能存在线性相关关系的数据，PCA能够把这组数据通过正交变换变成各个维度之间线性无关的数据，经过PCA处理的数据中的各个样本之间的关系往往更直观，所以它是一种非常常用的数据分析和预处理工具。PCA处理之后的数据各个维度之间是线性无关的，通过剔除方差较小的那些维度上的数据，我们可以达到数据降维的目的。

　　PCA从原始变量出发，通过旋转变化（即原始变量的线性组合）构建出一组新的，互不相关的新变量，这些变量尽可能多的解释原始数据之间的差异性（即数据内在的结构），他们就成为原始数据的主成分。由于这些变量不相关，因此他们无重叠的各自解释一部分差异性。依照每个变量解释时差异性大小排序，他们成为第一主成分，第二主成分，以此类推。

　　主成分分析（PCA）是一种基于变量协方差矩阵对数据进行压缩降维，去噪的有效方法，PCA的思想是将n维特征映射到k维上（k<n），这k维特征称为主元（主成分），是旧特征的线性组合，这些线性组合最大化样本方差，尽量使用新的k个特征互不相关。这k维是全新的正交特征，是重新构造出来的k维特征，而不是简单地从n维特征中取出其余n-k维特征。

　　说了这么多，下面说一下PCA降维的算法步骤。

　　设有m条n维数据：

• 1） 将原始数据按列组成n行m列矩阵X
• 2）将X的每一行（代表一个属性字段）进行零均值化（去平均值），即减去这一行的均值
• 3）求出协方差矩阵  C= 1/m*X*X^T  
• 4）求出协方差矩阵的特征值及对应的特征向量
• 5）将特征向量按对应特征值大小从上到下按行排列成矩阵，取前k行组成矩阵P（保留最大的k各特征向量）
• 6）Y=PX 即为降维到K维后的数据

 

五，核主成分分析KPCA介绍

　　在上面的PCA算法中，我们假设存在一个线性的超平面，可以让我们对数据进行投影。但是有些时候，数据不是线性的，不能直接进行PCA降维。这里就需要用到和支持向量机一样的核函数的思想，先把数据集从 n 维映射到线性可分的高维 N>n，然后再从N维降维到一个低维度 n'，这里的维度之间满足 n' < n< N。

　　使用了核函数的主成分分析一般称之为核主成分分析（Kernelized  PCA，以下简称 KPCA。假设高维空间的数据是由 n 维空间的数据通过映射 Φ 产生）。

　　则对于 n 维空间的特征分解：

 

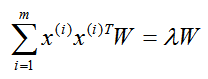
 　映射为：

 

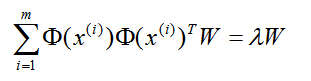
 　　通过在高维空间进行协方差矩阵的特征值分解，然后用和PCA一样的方法进行降维。一般来说，映射 Φ 不用显式的计算，而是在需要计算的时候通过核函数完成。由于KPCA需要核函数的运算，因此它的计算量要比PCA大很多。

六，PCA算法总结

　　这里对PCA算法做一个总结，作为一个非监督学习的降维方法，它只需要特征值分解，就可以对数据进行压缩，去噪。因此在实际场景应用很广泛。为了克服PCA一些缺点，出现了很多PCA的变种，比如上面为解决非线性降维的KPCA，还有解决内存限制的增量PCA方法 Incremental  PCA，以及解决稀疏数据降维的PCA方法Sparse  PCA等。

　　PCA算法的主要优点：

• 1）仅仅需要以方差衡量信息量，不受数据集以外的因素影响
• 2）各主成分之间正交，可消除原始数据成分间的互相影响的因素
• 3）计算方法简单，主要运算是特征值分解，易于实现

　　PCA算法的主要缺点：

• 1）主成分各个特征维度的含义具有一定的模糊性，不如原始样本特征的解释性强
• 2）方差小的非主成分也可能含有对样本差异的重要信息，因降维丢弃可能对后续数据处理有影响

七，实例PCA计算过程

　　现在假设有一组数据如下：

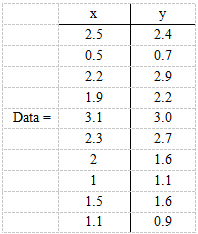
　　行代表了样例，列代表了特征，这里有10个样例，每个样例两个特征，可以这样认为，有10篇文档，x是10篇文档中“learn”出现的TF-IDF，y是10篇文档中“study”出现的IF_IDF。

　　第一步，分别求x和y的平均值，然后对所有的样例，都减去对应的均值。这里x的均值为1.81，y的均值为1.91，那么第一个一个样例减去均值后为（0.69,0.49），以此类推得到：

 

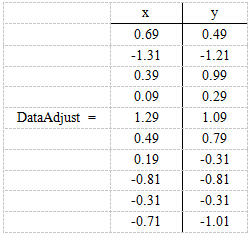
　　第二步，计算特征协方差矩阵，如果数据是三维的，那么协方差矩阵为：

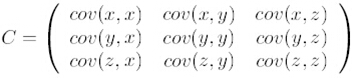
　　这里是2维的，只有x和y，求解得：

　　

　　对角线上分别是x和y的方差，非对角线上是协方差。协方差是衡量两个变量同时变化的变化程度。协方差大于0表示x和y若一个增加，另一个也增加；协方差小于0宝石一个增加，则另一个减少。如果x和y是统计独立的，那么二者之间的协方差就是0；但是协方差是0 ，并不能说明x和y是独立的。协方差绝对值越大，两者对彼此的影响越大，反之越小。协方差是没有单位的量，因此，如果同样的两个变量所采用的量纲发生变化，他们的协方差也会产生数值上的变化。

 

　　第三步，计算协方差矩阵的特征向量和特征值，选取特征向量

 

　　 　　上面两个特征值，下面是对应的特征向量，特征值0.490833989对应的特征向量是（-0.735178656, 0.677873399），这里的特征向量是正交的、归一化的，即长度为1。

 

　　第四步，将特征值按照从大到小的顺序排序，选择其中最大的k个，然后将其对应的k各特征向量分别作为列向量组成特征向量矩阵。

 

　　如果数据中有n维，计算出n个特征向量和特征值，选择前k个特征向量，然后最终的数据集合只有k维，取的特征向量命名为FeatureVector。 

  　  

　　这里的特征值只有两个，我们选择其中最大的那个，这里是1.28402771，对应的特征向量是(-0.677873399, -0.735178656)T。 

　　第五步，将样本点投影到选取的特征向量上，得到新的数据集

　　假设样例数为m，特征数为n，减去均值后的样本矩阵为DataAdjust(m*n)，协方差矩阵是n*n，选取的k个特征向量组成的矩阵为EigenVectors(n*k)。那么投影后的数据FinalData为

　　得到结果为

　　

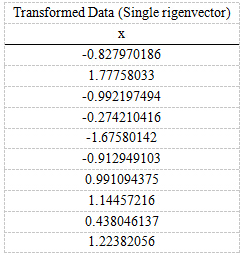
　　这样，就将原始样例的n维特征变成了k维，这k维就是原始特征在k维上的投影。

　　代码如下：

from  numpy  import *

li = [[2.5,2.4],[0.5,0.7],[2.2,2.9],[1.9,2.2],[3.1,3.0],[2.3,2.7],[2.0,1.6],[1.0,1.1],[1.5,1.6],[1.1,0.9]]
matrix = mat(li)
# 求均值
mean_matrix = mean(matrix,axis=0)
# print(mean_matrix)    #[[1.81 1.91]]
# 减去平均值
Dataadjust = matrix - mean_matrix
# print(Dataadjust)
'''
[[ 0.69  0.49]
 [-1.31 -1.21]
 [ 0.39  0.99]
 [ 0.09  0.29]
 [ 1.29  1.09]
 [ 0.49  0.79]
 [ 0.19 -0.31]
 [-0.81 -0.81]
 [-0.31 -0.31]
 [-0.71 -1.01]]
'''
#计算特征值和特征向量
covMatrix = cov(Dataadjust,rowvar=0)
# print(covMatrix)
'''
[[0.61655556 0.61544444]
 [0.61544444 0.71655556]]
'''
eigValues , eigVectors = linalg.eig(covMatrix)
# print(eigValues)
# print(eigVectors)
'''
[0.0490834  1.28402771]

[[-0.73517866 -0.6778734 ]
 [ 0.6778734  -0.73517866]]'''
# 对特征值进行排序
eigValuesIndex = argsort(eigValues)
# print(eigValuesIndex)
# 保留前K个最大的特征值
eigValuesIndex = eigValuesIndex[:-(1000000):-1]
# print(eigValuesIndex)
# 计算出对应的特征向量
trueEigVectors = eigVectors[:,eigValuesIndex]
# print(trueEigVectors)
'''
[[-0.6778734  -0.73517866]
 [-0.73517866  0.6778734 ]]
 '''
# # 选择较大特征值对应的特征向量
maxvector_eigval = trueEigVectors[：，0]
# print(maxvector_eigval)
'''
[-0.6778734  -0.73517866]
'''
# # 执行PCA变换：Y=PX 得到的Y就是PCA降维后的值 数据集矩阵
pca_result = maxvector_eigval * Dataadjust.T
# print(pca_result)
'''
[[-0.82797019  1.77758033 -0.99219749 -0.27421042 -1.67580142 -0.9129491
   0.09910944  1.14457216  0.43804614  1.22382056]]
'''

　　

　　上面的数据可以认为是learn和study特征融合为一个新的特征叫LS特征，该特征基本上代表了这两个特征，该过程如下图所示：

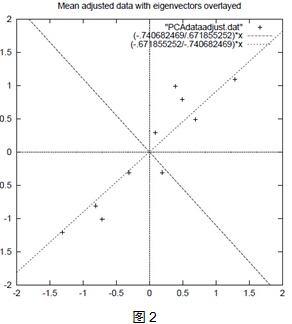
　　正号表示预处理后的样本点，斜着的两条线就分别是正交的特征向量（由于协方差矩阵是对称的，因此其特征向量正交），最后一句矩阵乘法就是将原始样本点分别往特征向量对应的轴上做投影，下图是FinalData根据最大特征值对应的特征向量转化回去后的数据集形式，可看出是将DataAdjust样本点分别往特征向量对应的轴上做投影：

　　

　　如果取的k=2，那么结果是

     

　　可见，若使用了所有特征向量得到的新的数据集，转化回去之后，与原来的数据集完全一样（只是坐标轴旋转）。

八，python实现主成分（PCA）降维

from numpy import *

def loadDataSet(fileName, delim='\t'):
    fr = open(fileName)
    stringArr = [line.strip().split(delim) for line in fr.readlines()]
    datArr = [map(float,line) for line in stringArr]
    return mat(datArr)

def pca(dataMat, topNfeat=999999):
    meanVals = mean(dataMat, axis=0)
    DataAdjust = dataMat - meanVals           #减去平均值
    covMat = cov(DataAdjust, rowvar=0)
    eigVals,eigVects = linalg.eig(mat(covMat)) #计算特征值和特征向量
    #print eigVals
    eigValInd = argsort(eigVals)
    eigValInd = eigValInd[:-(topNfeat+1):-1]   #保留最大的前K个特征值
    redEigVects = eigVects[:,eigValInd]        #对应的特征向量
    lowDDataMat = DataAdjust * redEigVects     #将数据转换到低维新空间
    reconMat = (lowDDataMat * redEigVects.T) + meanVals   #重构数据，用于调试
    return lowDDataMat, reconMat

　　测试数据testSet.txt由1000个数据点组成。下面对数据进行降维，并用matplotlib模块将降维后的数据和原始数据一起绘制出来。

（链接：https://pan.baidu.com/s/19k4ND3ISUjhfWZhj4Fhcbw 提取码：r3n7 ）

数据：（此数据直接复制可能无法使用，会报错， could not convert string to float，建议最好下载，或者去我的GitHub拿：https://github.com/LeBron-Jian/MachineLearningNote）

import matplotlib
import matplotlib.pyplot as plt

dataMat = loadDataSet('testSet.txt')
lowDMat, reconMat = pca(dataMat,1)
print "shape(lowDMat): ",shape(lowDMat)

fig = plt.figure()
ax = fig.add_subplot(111)
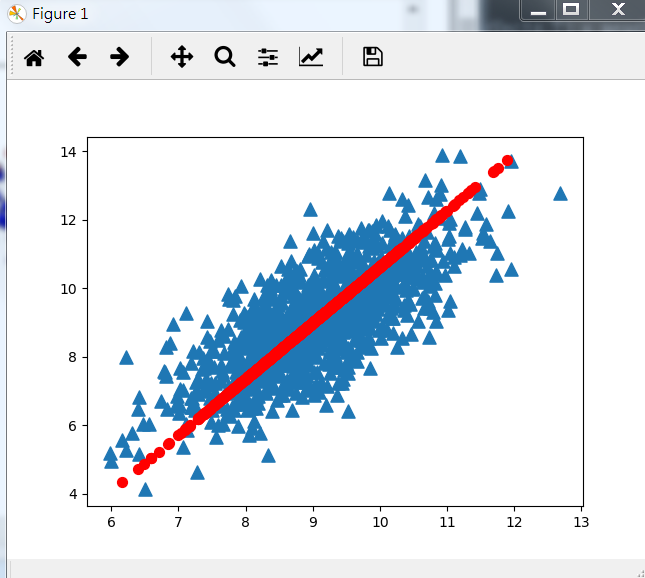
ax.scatter(dataMat[:,0].flatten().A[0],dataMat[:,1].flatten().A[0],marker='^',s=90)
ax.scatter(reconMat[:,0].flatten().A[0],reconMat[:,1].flatten().A[0],marker='o',s=50,c='red')
plt.show()

　　

结果如下图：

 九，sklearn实现PCA降维

　　　　在scikit-learn中，与PCA相关的类都在sklearn.decomposition包中。最常用的PCA类就是sklearn.decomposition.PCA，我们下面主要也会讲解基于这个类的使用的方法。

　　　　除了PCA类以外，最常用的PCA相关类还有KernelPCA类，在上面我们也讲到了，它主要用于非线性数据的降维，需要用到核技巧。因此在使用的时候需要选择合适的核函数并对核函数的参数进行调参。

　　　　另外一个常用的PCA相关类是IncrementalPCA类，它主要是为了解决单机内存限制的。有时候我们的样本量可能是上百万+，维度可能也是上千，直接去拟合数据可能会让内存爆掉， 此时我们可以用IncrementalPCA类来解决这个问题。IncrementalPCA先将数据分成多个batch，然后对每个batch依次递增调用partial_fit函数，这样一步步的得到最终的样本最优降维。

　　　　此外还有SparsePCA和MiniBatchSparsePCA。他们和上面讲到的PCA类的区别主要是使用了L1的正则化，这样可以将很多非主要成分的影响度降为0，这样在PCA降维的时候我们仅仅需要对那些相对比较主要的成分进行PCA降维，避免了一些噪声之类的因素对我们PCA降维的影响。SparsePCA和MiniBatchSparsePCA之间的区别则是MiniBatchSparsePCA通过使用一部分样本特征和给定的迭代次数来进行PCA降维，以解决在大样本时特征分解过慢的问题，当然，代价就是PCA降维的精确度可能会降低。使用SparsePCA和MiniBatchSparsePCA需要对L1正则化参数进行调参。

9.1 sklearn.decomposition.PCA参数介绍

　　　　下面我们主要基于sklearn.decomposition.PCA来讲解如何使用scikit-learn进行PCA降维。PCA类基本不需要调参，一般来说，我们只需要指定我们需要降维到的维度，或者我们希望降维后的主成分的方差和占原始维度所有特征方差和的比例阈值就可以了。

　　　　现在我们对sklearn.decomposition.PCA的主要参数做一个介绍：

　　　　1）n_components：这个参数可以帮我们指定希望PCA降维后的特征维度数目。最常用的做法是直接指定降维到的维度数目，此时n_components是一个大于等于1的整数。当然，我们也可以指定主成分的方差和所占的最小比例阈值，让PCA类自己去根据样本特征方差来决定降维到的维度数，此时n_components是一个（0，1]之间的数。当然，我们还可以将参数设置为"mle", 此时PCA类会用MLE算法根据特征的方差分布情况自己去选择一定数量的主成分特征来降维。我们也可以用默认值，即不输入n_components，此时n_components=min(样本数，特征数)。

　　　　2）whiten ：判断是否进行白化。所谓白化，就是对降维后的数据的每个特征进行归一化，让方差都为1.对于PCA降维本身来说，一般不需要白化。如果你PCA降维后有后续的数据处理动作，可以考虑白化。默认值是False，即不进行白化。

　　　　3）svd_solver：即指定奇异值分解SVD的方法，由于特征分解是奇异值分解SVD的一个特例，一般的PCA库都是基于SVD实现的。有4个可以选择的值：{‘auto’, ‘full’, ‘arpack’, ‘randomized’}。randomized一般适用于数据量大，数据维度多同时主成分数目比例又较低的PCA降维，它使用了一些加快SVD的随机算法。 full则是传统意义上的SVD，使用了scipy库对应的实现。arpack和randomized的适用场景类似，区别是randomized使用的是scikit-learn自己的SVD实现，而arpack直接使用了scipy库的sparse SVD实现。默认是auto，即PCA类会自己去在前面讲到的三种算法里面去权衡，选择一个合适的SVD算法来降维。一般来说，使用默认值就够了。

　　　　除了这些输入参数外，有两个PCA类的成员值得关注。第一个是explained_variance_，它代表降维后的各主成分的方差值。方差值越大，则说明越是重要的主成分。第二个是explained_variance_ratio_，它代表降维后的各主成分的方差值占总方差值的比例，这个比例越大，则越是重要的主成分。

9.2 PCA实例

　　下面学习一个示例。

　　首先我们生成随机数据并可视化，代码如下：

import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
from sklearn.datasets.samples_generator import make_blobs

# X为样本特征，Y为样本簇类别， 共1000个样本，每个样本3个特征，共4个簇
X, y = make_blobs(n_samples=10000, n_features=3, centers=[[3, 3, 3], [0, 0, 0], [1, 1, 1], [2, 2, 2]],
                  cluster_std=[0.2, 0.1, 0.2, 0.2],
                  random_state=9)
fig = plt.figure()
ax = Axes3D(fig, rect=[0, 0, 1, 1], elev=30, azim=20)
plt.scatter(X[:, 0], X[:, 1], X[:, 2], marker='o')

 　　生成的图如下：

 　　我们先不降维，只对数据进行投影，看看投影后的三个维度的方差分析，代码如下：

pca = PCA(n_components=3)
pca.fit(X)
print(pca.explained_variance_ratio_)
print(pca.explained_variance_)
# [0.98318212 0.00850037 0.00831751]
# [3.78521638 0.03272613 0.03202212]

 　　可以看出投影后三个特征维度的方差比例大约为 0.983,  0.08， 0.08。投影后第一个特征占了绝大多数的主成分比例。

　　现在我们开始进行降维，从三维降到二维，代码只需要换参数即可，我们看结果：

[0.98318212 0.00850037]
[3.78521638 0.03272613]

 　　这个结果其实是可以语料的，因为上面三个投影后的特征维度的方差分别为 [3.78521638 0.03272613 0.03202212] ，投影到二维后选择的肯定是前两个特征，而抛弃第三个特征。

　　为了有个直观的认识，我们看看此时转换后的数据分布，代码如下：

X_new = pca.transform(X)
plt.scatter(X_new[:, 0], X_new[:, 1], marker='o')
plt.show()

 　　输出图如下：

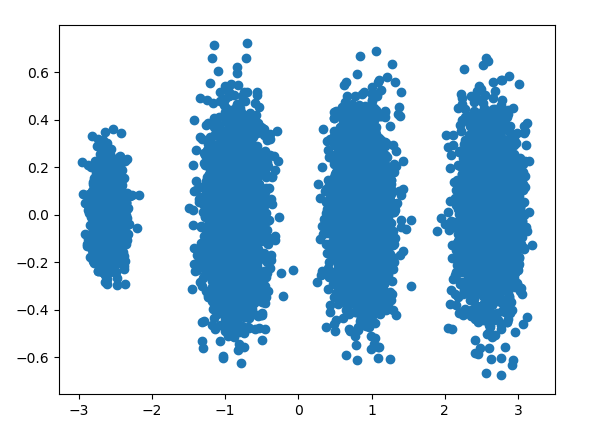
 　　可见降维后的数据依然可以很清楚的看到我们之前三维图中的四个簇。

　　现在我们看看不直接指定降维的维度，而指定降维后的主成分方差和比例。

pca = PCA(n_components=0.95)
pca.fit(X)
print(pca.explained_variance_ratio_)
print(pca.explained_variance_)
print(pca.n_components_)
# [0.98318212]
# [3.78521638]
# 1

 　　我们指定了主成分至少占 95% ，输出如上，可见只有第一个投影特征被保留，其实也很好理解，我们的第一个主成分占投影特征的方差比例高达 98 %，只选择这一个特征便可以满足 95%的阈值。我们现在选择阈值 99%看看：

[0.98318212 0.00850037]
[3.78521638 0.03272613]
2

 　　其实这个也很好理解，因为我们第一个主成分占了 98.3% 的方差比例，第二个主成分占了0.08的方差比例，两者一起就可以满足我们的阈值。

　　最后我们看看让 MLE算法自己选择降维维度的效果，代码如下：

pca = PCA(n_components='mle')
pca.fit(X)
print(pca.explained_variance_ratio_)
print(pca.explained_variance_)
print(pca.n_components_)
# [0.98318212]
# [3.78521638]
# 1

 　　可见，由于我们数据的第一个投影特征的方差占比高达 98.3%，MLE算法只保留了我们第一个特征。

 

 参考文献：

http://www.360doc.com/content/13/1124/02/9482_331688889.shtml

 http://www.docin.com/p-160874280.html

https://www.zhihu.com/question/54100505/answer/432025686

https://www.cnblogs.com/pinard/p/6243025.html