快速傅里叶变换(FFT)初学笔记
懵了一整天,总算懵出一点东西来
发觉 \(\mbox{FFT}\) 是个好东西,但是网上的讲解都太过模糊,对于本人这种连卷积是什么都还不清楚的蒟蒻,讲得太过深奥,经过一天的努力
(包括划水),鄙人记录了这样一篇学习笔记。
关于卷积
本蒟蒻一直觉得这个概念很抽象,下面的东西接近虚构,只是笔者个人的感性理解。
假设有两个多项式 \(\mbox F(x)\) 和 \(\mbox G(x)\)
记 \(\mbox H(x)\) 为它们的卷积,则 \(\mbox H(x)=\mbox F(x) \ *\ \mbox G(x)\)。(还用你说)
常见的卷积形式是:\(\mbox H(x)=\sum f(x_i)\times g(x_{n-i})\)。
另外,莫比乌斯反演也是一种特殊卷积的形式:\(g(x)=\underset{d|x}{\sum}\mu(d)\times f(\frac{x}{d})\)
懵了没关系,后面还勉强
关于FFT
以朴素的做法,计算一次卷积所用的时间为 \(\mbox O(n^2)\) ,吃不消,所以要用 \(\mbox{FFT}\)
快速傅里叶变换 (\(Fast\ Fourier\ Transform\)),简称 \(\mbox{FFT}\),是一种快速求解多项式卷积的方法。
多项式表示法
了解多项式表示法,是学习 \(\mbox{FFT}\) 的基础。
\(\color{red}\P\) 系数表示法
假设存在多项式 \(A\) ,使得:
那么可以将 \(A\) 用系数表示法表示出来:
这样来计算 \(A\) 和 \(B\) 的卷积,需要便利 \(A\) ,\(B\) 的所有元素,时间复杂度 \(\mbox O(n^2)\)
$\color{red}{\P} $ 点值表示法
视野放到坐标轴中。
将多项式看作一个函数,将选定的值带入到这个函数中,算出相应的值:
那么相乘就只需要 \(\mbox O(n)\) 的复杂度:
但是由于我们需要枚举 \(x\) 的值,所以总的时间复杂度没有变,还是 \(\mbox O(n^2)\)
要是我们能获取一些特殊而方便的值,方便运算,就能优化掉枚举所用的时间复杂度了。
在想下去之前,有点前置知识要先声明一下:
复数
一个复数可以表示为 \(z=a+bi(a,b\in \R)\) 。其中,\(i\) 是虚数的单位,满足 \(i^2=-1\)。\(a\) 被称为实部,\(b\) 被称为虚部。
在坐标轴中,复数可表示为一个点,其中,数轴的横轴为实部,纵轴为虚部。例如 \(z=3+\sqrt{3}i\) 在坐标轴上就是 \((3,\sqrt{3})\)。
这个点到原点的距离叫做这个复数的模,它与 \(x\) 轴正方向的夹角叫做这个复数的角度。
因此,复数 \(z=3+\sqrt3i\) 也可以用极坐标表示为 \((2\sqrt3,\frac{\pi}{6})\),即(模,角度)
一个复数也可以看作一个向量,因此它满足向量运算的平行四边形法则:
令 \(z_1=a+bi, z_2=c+di\)
\(z_1+z_2=(a+c)+(b+d)i\)
\(z_1-z_2=(a-c)+(b-d)i\)
\(z_1\times z_2=(ac-bd)+(ad+bc)i\)
极坐标乘法:
令 \(z_1(z_1,\theta_1),z_2(a_2,\theta_2)\)
\(z_1\times z_2=(a_1a_2,\theta_1+\theta_2)\)
我们想要带入求值,快速算出 \(x^0,x^1,x^2,\dots,x^{n-1}\) 。比如 \(1\) , \(-1\) , \(i\) , \(-i\) 这样的数就挺好,可惜数量太少。
所以某位大胆的科学家(傅里叶)将目光转向坐标轴上的圆。
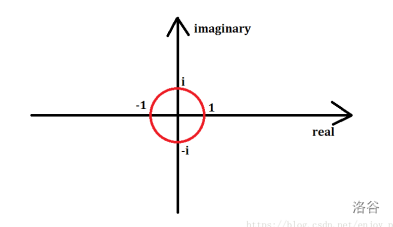
\(\mbox{STL}\) 里面专门有一个模板 complex<T> ,T 支持double,long double和float。我喜欢直接调用,也可以自己写:
#include<complex>
using namespace std;
using cp=complex<double>;
\(\color{red}{\P}\) \(n\) 次单位根
以下默认 \(n\) 为 \(2\) 的整数次幂
- 表示:\(\omega_n^1\)
- 将单位圆等分成 \(n\) 分,从 \((1,0)\) 开始,逆时针从 \(0\) 号开始标号,一直标到 \(n-1\)号,记编号为 \(k\) 的复数为 \(\omega _n^k\),其中复数 \(\omega_n^1\) 被称为 \(n\) 次单位根
- 极坐标 \(\omega_n^k=(1,\frac{k}{n}2\pi)\)
- \((\omega_n^1)^k=\omega_n^k\)
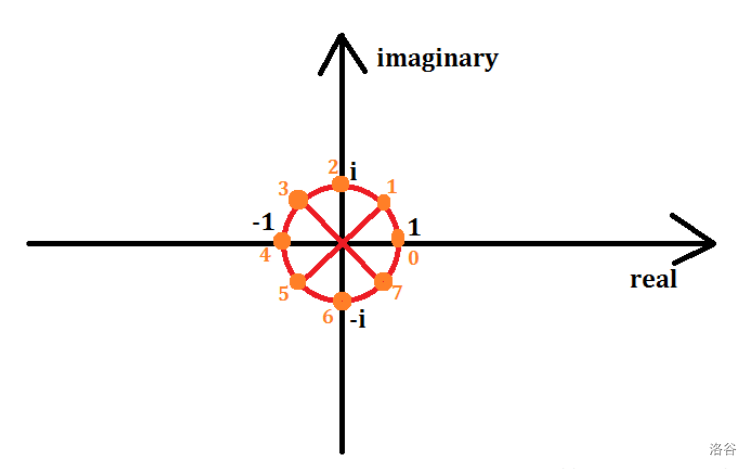
\(\color{red}{\P}\) 要用到的单位根的一些性质
首先你要知道,\(\omega_{dn}^{dk}=\omega_n^k\)
证明
\(\omega_{dn}^{kn}=\cos\frac{dk}{dn}2\pi+i\ \sin\frac{dk}{dn}2\pi=\cos\frac{k}{n}2\pi+i\ \sin\frac{k}{n}2\pi=\omega_n^k\)
证毕
其次,还有很重要的一点,\(w_{n}^{k+\frac{n}{2}}=\omega_n^k\)
证明
\(\omega_n^{\frac{n}{2}}=\cos\frac{\frac{n}{2}}{n}2\pi+i\ \sin\frac{\frac{n}{2}}{n}2\pi=\cos\pi+i\ \sin\pi=-1\)
\(\omega_n^{k+\frac{n}{2}}=\omega_n^k\times\omega_n^{\frac{n}{2}}=-\omega_{n}^k\)
也可以从上图中看出。
证毕
\(\omega_n^k\) 的模长为 \(|\omega_n^k|=\cos^2\frac{k}{n}2\pi+\sin^2\frac{k}{n}2\pi=\color{red}1\)
FFT 具体算法
\(\color{red}{\P}\) 从系数到点值(DNT)
\(n=2^k,k\in\Z\),不足的用 \(0\) 补位。
显然,\(A(x)\) 可以分为两部分:
将 \(w_n^k(k<\frac{n}{2})\) 带入 \(A\) 中
\(A(\omega_n^k)=A_1((\omega_n^k)^2)+\omega_n^kA_2((\omega_n^k)^2)=A_1(\omega_n^{2k})+\omega_n^kA_2(\omega_n^{2k})=A_1(\omega_{\frac{n}{2}}^k)+\omega_n^kA_2(\omega_{\frac{n}{2}}^k)\)
与之类似,你会发现:
\(A(\omega_n^{k+\frac{n}{2}})=A_1(\omega_{\frac{n}{2}}^k)-\omega_n^kA_2(\omega_{\frac{n}{2}}^k)\)
如果我们将 \(A_1(\omega_{\frac{n}{2}}^k)\) 和 \(A_2(\omega_{\frac{n}{2}}^k)\) 求出来,似乎问题就迎刃而解了。
而 \(A_1,A_2\) 也可以通过上述做法求得。
\(\color{red}{\P}\) 从点值到系数(IDNT)
非常玄幻,只能浅浅过一下。
其实 \(\mbox{DFT}\) 可以写成矩阵积的形式 \(y=V_na\) ,其中 \(V_n\) 是一个由 \(\omega_n^k\) 组成的范德蒙德矩阵。
这个矩阵具体是什么先不讨论,它大概长这个样。
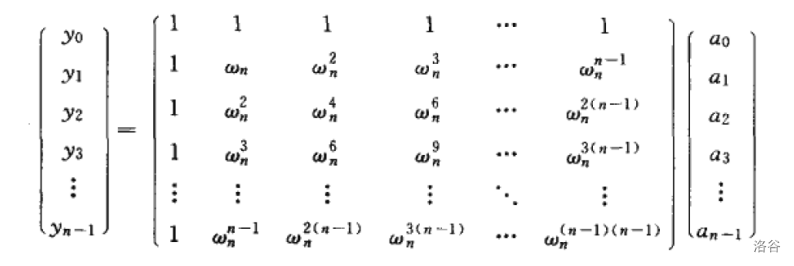
\(\mbox{FFT}\) 已经完成了 \(\mbox{DNT}\) 的一步,但是此时我们所拥有的是点值,为了方便运算,我们还要将其转换回系数。
作为 \(\mbox{DNT}\) 的逆变换 \(\mbox{IDNT}\) ,我们只需要找到相应的矩阵 \(V_n^{-1}\) ,使得 \(V_n^{-1}V_n=I_n\) ( \(I_n\) 为一个 \(n\times n\) 的单位矩阵 )
给出一个定理:
\(V_n^{-1}\) 中 \((j,k)\) 处的元素为 \(\frac{\omega_n^{-jk}}{n}\)
证明太显然复杂,读者可自行手模或上网求证。
对比发现,\(V_n\) 中 \((j,k)\) 处的元素为 \(\omega_n^{jk}\) ,\(V_n^{-1}\) 中 \((j,k)\) 中元素为 \(\frac{\omega_n^{-jk}}{n}\)
似乎只差一个符号与一次除法。
所以我们通常将 \(\mbox{DFT}\) 和 \(\mbox{IDFT}\) 作为同一个函数。
\(\color{red}\P\) 递归代码解析
void FFT(int len,cp a[],int type){//要处理的数组长度,数组,符号+1或-1
if(len==1)return ;//递归边界
int tmp=len>>1;
cp b[tmp+5],c[tmp+5];
for(int i=0;i<=len;i+=2)
b[i>>1]=a[i],c[i>>1]=a[i+1];
FFT(tmp,b,type);
FFT(tmp,c,type);//分治
cp I(cos(2*Pi/len),type*sin(2*Pi/len)),w(1,0);
for(int i=0;i<tmp;++i,w*=I){
a[i]=b[i]+w*c[i];
a[i+tmp]=b[i]-w*c[i];
}
}
注意,len 必须为 \(2\) 的整数次幂,不足的用 \(0\) 补位。
在 main() 函数中:
int n,m;cin>>n>>m;
for(int i=0;i<=n;++i){int x;cin>>x;f[i].real(x);}
for(int i=0;i<=m;++i){int x;cin>>x;g[i].real(x);}
int len=1;while(len<=n+m)len<<=1;
FFT(len,f,1);
FFT(len,g,1);
for(int i=0;i<=len;++i)f[i]*=g[i];
FFT(len,f,-1);
for(int i=0;i<=n+m;++i)printf("%.0f ",f[i].real()/len+0.5);
但是,这份代码虽然便于理解,但是递归来递归去常数太大了,没准哪一天就 \(\mbox{TLE}\)。
所以我们需要优化。
\(\color{red}\P\) 非递归代码解析
观察 \(A\) 的遍历顺序,设 \(n=2^3=8\)
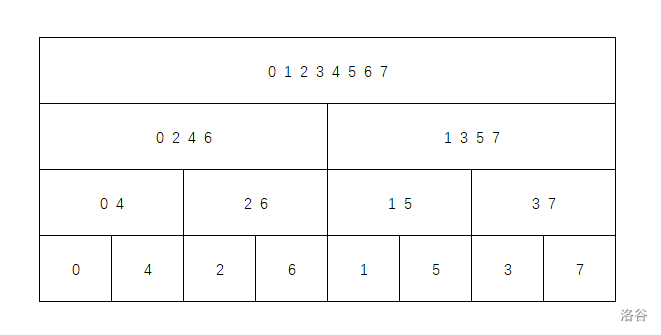
排在第 \(0\) 位的是 \(0\) ,\(0\) 的二进制串为 \(000\)。
排在第 \(1\) 位的是 \(4\) ,\(1\) 的二进制串为 \(001\),\(4\) 的二进制串为 \(100\)。
排在第 \(2\) 位的是 \(2\) ,\(2\) 的二进制串为 \(010\)。
排在第 \(3\) 位的是 \(6\) ,\(3\) 的二进制串为 \(011\),\(6\) 的二进制串为 \(110\)。
排在第 \(4\) 位的是 \(1\) ,\(4\) 的二进制串为 \(100\),\(1\) 的二进制串为 \(001\)。
排在第 \(5\) 位的是 \(5\) ,\(5\) 的二进制串为 \(101\)。
排在第 \(6\) 位的是 \(3\) ,\(6\) 的二进制串为 \(110\),\(3\) 的二进制串为 \(011\)。
排在第 \(7\) 位的是 \(7\) ,\(7\) 的二进制串为 \(111\)。
发现什么规律了吗?
二进制翻转:
int len=1,cnt=0;while(len<=n+m)len<<=1,++cnt;
for(int i=0;i<len;++i)rev[i]=rev[i>>1]>>1|(i&1)<<cnt-1;
有了这个预处理,我们就不需要一层一层往下递归,只需要一层一层往上递推就行了:
void FFT(int len,cp a[],int type){
for(int i=0;i<len;i++)
if(i<rev[i])swap(a[i],a[rev[i]]);
for(int i=1;i<len;i<<=1){
cp I(cos(Pi/i),type*sin(Pi/i));
for(int j=0;j<len;j+=i<<1){
cp w(1,0);
for(int k=0;k<i;k++,w*=I){
cp x=a[j+k],y=w*a[i+j+k];
a[j+k]=x+y;
a[i+j+k]=x-y;
}
}
}
}
模板题
#include<complex>
#include<cmath>
#include<cstdio>
#include<iostream>
using namespace std;
using cp=complex<double>;
const int Maxn=2e6+1e5;
const double Pi=acos(-1);
int rev[Maxn];
cp f[Maxn];
cp g[Maxn];
void FFT(int len,cp a[],int type){
for(int i=0;i<len;i++)
if(i<rev[i])swap(a[i],a[rev[i]]);
for(int i=1;i<len;i<<=1){
cp I(cos(Pi/i),type*sin(Pi/i));
for(int j=0;j<len;j+=i<<1){
cp w(1,0);
for(int k=0;k<i;k++,w*=I){
cp x=a[j+k],y=w*a[i+j+k];
a[j+k]=x+y;
a[i+j+k]=x-y;
}
}
}
}
int main(){
int n,m;cin>>n>>m;
for(int i=0;i<=n;++i){int x;cin>>x;f[i].real(x);}
for(int i=0;i<=m;++i){int x;cin>>x;g[i].real(x);}
int len=1,cnt=0;while(len<=n+m)len<<=1,++cnt;
for(int i=0;i<len;++i)rev[i]=rev[i>>1]>>1|(i&1)<<cnt-1;
FFT(len,f,1);FFT(len,g,1);
for(int i=0;i<=len;++i)f[i]*=g[i];
FFT(len,f,-1);
for(int i=0;i<=n+m;++i)cout<<(int)(f[i].real()/len+0.5)<<' ';
return 0;
}
Luogu P1919 【模板】A*B Problem 升级版
其实整数也可以看作 \(x=10\) 的多项式
#include<complex>
#include<cmath>
#include<cstdio>
#include<iostream>
#include<string>
using namespace std;
using cp=complex<double>;
const int Maxn=3e6+5;
const double Pi=acos(-1);
int rev[Maxn];
void FFT(int len,cp a[],int type){
for(int i=0;i<=len;i++)
if(i<rev[i])swap(a[i],a[rev[i]]);
for(int i=1;i<len;i<<=1){
cp I(cos(Pi/i),type*sin(Pi/i));
for(int j=0;j<len;j+=i<<1){
cp w(1,0);
for(int k=0;k<i;++k,w*=I){
cp x=a[j+k],y=w*a[i+j+k];
a[j+k]=x+y;a[i+j+k]=x-y;
}
}
}
}
cp a[Maxn],b[Maxn];
int ans[Maxn];
int main(){
string s,t;cin>>s>>t;
int n=-1,m=-1;
for(int i=s.length()-1;~i;--i)a[++n]=s[i]^48;
for(int i=t.length()-1;~i;--i)b[++m]=t[i]^48;
int len=1,cnt=0;
while(len<=n+m)len<<=1,++cnt;
for(int i=0;i<=len;++i)
rev[i]=rev[i>>1]>>1|(i&1)<<cnt-1;
FFT(len,a,1);FFT(len,b,1);
for(int i=0;i<=len;++i)a[i]*=b[i];
FFT(len,a,-1);
for(int i=0;i<=len;++i){
ans[i]+=(int)(a[i].real()/len+0.5);
if(ans[i]>=10){
ans[i+1]+=ans[i]/10;
ans[i]%=10;
len+=(i==len);
}
}
while(!ans[len]&&len>=1)--len;
while(len>=0)cout<<ans[len--];
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号