为了求个素数，科学家们也是蛮拼的

0.素数筛选之大难题

---

 　　题目非常简单：

输入一个N，判断从0~N有多少个素数

　　至于数据范围：

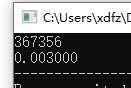
0≤N≤367356

　　素数是个迷人的东西，哥德巴赫猜想就诞生在它身上。素数无法使用那些智障般的判断法则，所以素数的判断更令人着迷。从古至今，多少科学家们为此前仆后继，从试数法，到线性筛，一步步彰显人类的智慧与数学的奥妙。

　　今天，就让我们一起从最远古的试数法开始，追溯前人，学习素数筛选法。

1.试数法

---

　

bool isPrime(int n){
    if(n<2)
        return false;
    
    for(int i=2;i<n;i++)
        if(n%i==0)
            return false;
    
    return true;
}

int main(){
    int n;
    scanf("%d",&n）；
    for(int i=2;i<=n;i++)
        if(isPrime(i))
             printf("%d ",i);
        return 0;  
}

　　故名思义，我从1~N把每个数都判断一下，这样的时间复杂度是喜闻乐见的O(n²)。为了让大家更直观的感受O(n²)之快，我们来做个小小的实验。

bool isPrime(int n){
    if(n<2)
        return false;
    
    for(int i=2;i<n;i++)
        if(n%i==0)
            return false;
    
    return true;
}

int size;

int main(){
    clock_t start,end;
    
    int n;
    scanf("%d",&n);
    start=clock();
    for(int i=2;i<=n;i++)
        if(isPrime(i))
//            printf("%d ",i);
            size++;
                
    end=clock();
    
    printf("%lf",(double)(end-start)/CLOCKS_PER_SEC);
    return 0;
}

 

　　　<附>clock()函数简单介绍

所需头文件：<time.h>或<ctime>

返回值类型：clock_t (long类型);

返回值：从开启这个程序进程到程序调用clock()函数之间的CPU时钟计时单元(clock tick)数（挂钟时间）。

例如：

int size;

int main(){
    clock_t start,end;
    
    int n;
    scanf("%d",&n);

    start=clock();
    printf("%lf\n",(double)start/CLOCKS_PER_SEC);
    
    for(int i=2;i<=n;i++)
        if(isPrime(i))
//            printf("%d ",i);
            size++;
                
    end=clock();
    printf("%lf\n",(double)end/CLOCKS_PER_SEC);

    return 0;
}

运行结果：

 输入：10000

输出：2.354000//从程序开始到start=clock()的用时

      2.270000//从程序开始到end=clock()的用时

CLOCKS_PER_SEC：常量，表示每一秒（per second）有多少个时钟计时单元

 　　看不懂倒也没关系，能读数便行

　　

　　看看运行结果：

                 

 

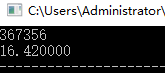
　　经过漫长的等待，我们发现，当N=367356,需要15~16秒钟，才能完成运行。

　　所以，我们需要优化算法。

2.试数法sqrt()优化

---

　　我们仔细思考：

　　一个合数n=a×b, 那么因数a,b一定存在于两个集合中，也就是[2，√n],[√n +1，n-1]。

　　如果你没听懂，读者自证不难。

　　总之：

 

bool isPrime(int n){
    if(n<2)
        return false;
        
    for(int i=2;i<=sqrt(n);i++)
        if(n%i==0)
            return false;
            
    return true;
}

int size;

int main(){
    clock_t start,end;
    
    int n;
    scanf("%d",&n);
    start=clock();


    for(int i=2;i<=n;i++)
        if(isPrime(i))
//            printf("%d ",i);
            size++;
                
    end=clock();

    printf("%lf",(double)(end-start)/CLOCKS_PER_SEC);
    return 0;
}

 

 

　　这时我们的时间复杂度已经非常可观：

　

　　O(√n)

　　但是，时间是有限的，优化是无限的

3.试数法sqrt()÷2优化

---

 

想一想：偶数之中，除了2都是合数。

于是我们可以尝试跳过偶数直接判断。

bool isPrime(int n){
    if(n<2)
        return false;
    for(int i=2;i<=sqrt(n);i++)
        if(n%i==0)
           return false;       
   return true;
}

int size;

int main(){
    clock_t start,end;

    int n;
    scanf("%d",&n);
    start=clock();
    size++;
    for(int i=3;i<=n;i+=2)
       if(isPrime(i))
//            printf("%d ",i);
            size++;
                 
    end=clock();
    
    printf("%lf",(double)(end-start)/CLOCKS_PER_SEC);
    return 0;
}

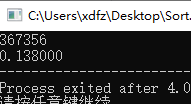
耗时有了微小的变化：

4.超高级的The Sieve of Eratosthenes(埃拉托斯特尼筛法)

---

名字听起来就很不错~

埃氏筛基本思想是这样的，如果我知道一个数 x 是素数，那么它的倍数一定是合数，也就是 2x, 3x, 4x, ... 都是合数。

举例说明：2 是素数，它的倍数们：4、6、8、10 等等，都是合数，这是显而易见的。

 假设从起点开始（起点可由要求指定）的所有数都是质数。从起点开始向前搜寻，若为质数，则将其倍数（不超过上界n）标记为非质数。例如2为质数，则标记4，6，8, ...这些2的倍数都为非质数，然后标记下一个……依此类推。

度娘曰：要得到自然数n以内的全部素数，必须把不大于 的所有素数的倍数剔除，剩下的就是素数。

详细过程如下：

　　现有一个数列[2,25]:

　　 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 

　　序列的第一个质数是2；

　　 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 

　　于是我们划去2的所有倍数；序列变成了：

　　 2 3 5 7 9 11 13 15 17 19 21 23 25 

　　如果这个序列中最大数小于最后一个标出的素数的平方，那么剩下的序列中所有的数都是素数，因为25大于2的平方，我们还要继续；

　　序列的下一个数是3，于是我们划去3的所有倍数：

　　 2 3 5 7 11 13 17 19 23 25 

　　因为25大于3的平方，所以我们继续算；再下一个数是5，于是我们划去5的所有倍数：

　　 2 3 5 7 11 13 17 19 23 

　　此时23小于5的平方，所以剩下的这一溜全是素数。

代码实现：

int size;
int vis[400010];

int main(){
    clock_t start,end;

    int n;
    scanf("%d",&n);
    start=clock();
    
    for(int i=2;i<=n;i++){
        if(vis[i]==true)continue;
        for(int j=i*2;j<=n;j+=i)
            vis[j]=true;
                size++;
    }
                 
    end=clock();
    
    printf("%lf",(double)(end-start)/CLOCKS_PER_SEC);
    return 0;
}

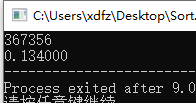
时间优化有了质的飞跃：

5.Leonhard Euler 的线性筛（欧拉筛）

---

 

欧拉，简直是数学史上的天神，他研究出的一笔画问题，欧拉回路问题，在信息学也有广泛的应用。

埃氏筛节省了许多时间，但用它筛去合数，必定有被重复筛去的部分，比如6，在筛2的倍数和筛3的倍数的过程中被重复筛去了。如果能让每个合数都只被标记一次，那么时间复杂度就可以降到O(n)了。

bool vis[N];
int Prime[N],size;
 
int main(){
    clock_t start,end;
    
    int n;
    scanf("%d",&n);
    start=clock();
    
    for(int i=2;i<=n;i++){
        if(!vis[i])Prime[++size]=i;
        for(int j=1;j<=size;j++){
            if(i*Prime[j]>n)break;
            vis[i*Prime[j]]=true;  //能由两个数相乘而得，这一定是合数 
            if(!(i%Prime[j]))break; //如果Prime[j]是i的因数，不妨留到下一次筛 
        }
    }
    
    end=clock();
    
    printf("%lf",(double)(end-start)/CLOCKS_PER_SEC);
    return 0;
}

为了让大家更好感受线性筛的筛法，我们修改修改代码：

bool vis[N];
int Prime[N],size;
 
int main(){
    int n;
    scanf("%d",&n);
    for(int i=2;i<=n/2;i++){
        if(!vis[i])Prime[++size]=i;
        printf("When i=%3d,the numbers given up are ",i);
        for(int j=1;j<=size;j++){
            if(i*Prime[j]>n)break;
            vis[i*Prime[j]]=true;
            printf("%3d,",i*Prime[j]);
            if(!(i%Prime[j]))break;
        }
        printf("\n");
    }
    return 0;
}

 

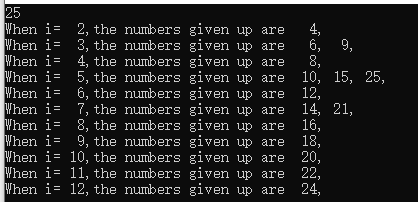
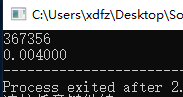
所用时间：

---

 

--Thank you--