流形学习之等距特征映射（Isomap）

　　感觉是有很久没有回到博客园，发现自己辛苦写的博客都被别人不加转载的复制粘贴过去真的心塞，不过乐观如我，说明做了一点点东西，不至于太蠢，能帮人最好。回校做毕设，专心研究多流形学习方法，生出了考研的决心。话不多说，看论文带大家走入Joshua B. Tenenbaum的Isomap的世界！

　　大数据时代的人总是那么的浮躁不安，高维并不可怕，事实的本质总是简单而单调的，因此流形学习理念中直接假设高维的数据都存在低维的本征结构。自“流形”这个概念被提出以来，许多人都在寻找一个高维数据中最现实的问题——降维（维数简约）。为在高维观察值中寻找有意义的低维，Tenenbaum提出“非线性降维的全局几何框架”计算出了全局最优解，并保证近似收敛到原始高维数据的真实结构。我这里不想翻译人家的东西，仅仅是将该算法接着前面说的研究生的数模题给出的数据来讲解，也是对作者本人的尊重（可以学习，但拒绝粘贴！）。

　　题目：3c.mat中的数据为两个人在不同光照下的人脸图像共20幅（X变量的每一列为拉成向量的一副人脸图像），请将这20幅头像分为两类。

　　思考1：不管如何，首先加载数据（load 3c.mat）看看这个3c.mat文件中到底是个神马数据

　　我们知道，这个数据的20个人脸（来源于两个人在不同光照下的照片），其中每一个人脸数据是经过拉长后的2016维的人脸头像数据，这样每一张图片就是一个2016维欧式空间的一个点。按照流形的定义，可以认为这两个人脸头像经过不同光照内嵌在2016维的高维空间中。因此需要降维到三维流形，三维流形中的三个变量分别是：人脸1、人脸2与不同的光照。

　　思考2：说道维数约简（降维技术哪家强），经典的降维技术就是主成分分析（PAC）和多维尺度分析（MDS）简单易行，并且能保证发现高维输入空间的位于线性子空间上的真实数据结构。其中PCA以方差的大小来衡量信息量的多少，认为方差正比的反应提供的信息量，其基本思想是通过线性变换尽可能地保留方差大的数据量。而MDS基本思想是在低维嵌入空间中尽量保持原始数据任意两点之间的欧式距离。但是，对于包含非线性结构的数据集而言，这两种方法往往是无效的，尤其是本题中的人脸数据集的内嵌的三个维度使用以上方法是徒劳的（无法线性表示，也无法使用欧式距离衡量点与点之间的距离）。这就轮到咱们流形学说的人出场啦～

　　思考3：其实线性流形方法无法在非线性流形上解决的问题，无非是需要解决两个问题：

　　1、如何测量流形上的几何距离？

　　2、如何将高维的2016维欧式空间映射到三维的低维空间？

　　首先，针对问题1，将MDS算法中的欧式距离换成“测地距离”，先抛一个“测地线的维基定义”。预热以后，我们来看经典的瑞士卷（图A），注意以下图A、B、C均来源于原文论文Fig3截图：

　　

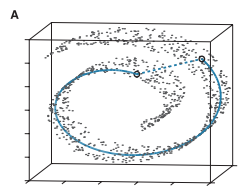
　　看到瑞士卷，我饿了》《，现在要我们把自己想象成是瑞士卷上的蚂蚁（对人类来说瑞士卷是三维的，对蚂蚁来说是二维的），上图A中的两个黑色圈圈为两只恩爱无比的蚂蚁，如何让这两只蚂蚁在最短的时间内见面呢？要走最短路径测地线蓝色线才是正道（直线最短？直接沿着虚线强行阔过去？你不想活了么？）因此，抛弃欧式距离，引来测地距离～

　　邻近点：直接计算邻近点之间的欧式空间距离

　　远距离的点：计算邻近点之间的最短距离连接成的序列，如下图所示（来源于博客），要计算空间中远距离的亮点1与9，计算1到9的最短路径1、2、3...9，沿着路径依次类推直到到达目的地9（根据流形中的全局非线性和局部线性属性）：

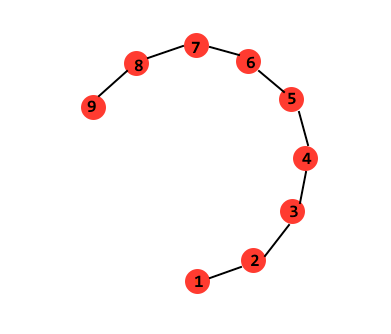
　　最后形成如下图所示的瑞士卷上的逼近测地线，如下图B中的红色线条所示：

　　

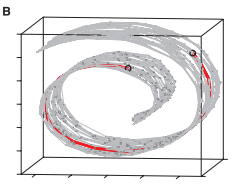
 　　实现方法：引入图论框架，将数据作为图中的点，点与其邻近点之间使用边来连接，逼近的测地线使用最短路径代替。

　　 Isomap算法如下：

　　 步骤1：构建邻接图G（复杂度：O（DN²））

　　 基于输入空间X中流形G上的的邻近点对i,j之间的欧式距离d_x (i,j)，选取每个样本点距离最近的K个点（K-Isomap）或在样本点选定半径为常数ε的圆内所有点为该样本点的近邻点，将这些邻近点用边连接，将流形G构建为一个反映邻近关系的带权流通图G；

　　 步骤2：计算所有点对之间的最短路径（复杂度：O（DN²））

　　 通过计算邻接图G上任意两点之间的最短路径逼近流形上的测地距离矩阵D_G={d_G(i,j)}，最短路径的实现以Floyd或者Dijkstra算法为主。

　　 步骤3：构建k维坐标向量（复杂度：O（dN²））

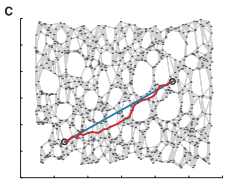
　　 根据图距离矩阵D_G={d_G(i,j)}使用经典Mds算法在d维空间Y中构造数据的嵌入坐标表示（如下图C所示），选择低维空间Y的任意两个嵌入坐标向量y_i与y_j使得代价函数最小：

　　

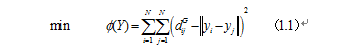
　　其中等式1.1的全局最优解可以通过将坐标向量y_i设置为距离矩阵D_G前d个特征值对应的特征向量来得到。

　　以上算法的实现可以通过主页：http://isomap.stanford.edu/访问获得，数模问题中的人像聚类的实现则是通过这一流形学习延伸出来的聚类算法K-manifolds实现，SSC算法的实现也可以给予参考，代码如下：

　　

%% 图c, ssc方法
load('3c.mat')
r = 0; affine = true; outlier = false; rho = 0.7; alpha=20;
[IDX, C1] = SSC(data,r,affine,alpha,outlier,rho,2);
for i=1:20
    subplot(4,5,i);
    pic = data(:,i);
    pic = reshape(pic,[42,48]);
    imshow(pic/256);
    if (IDX(i)==1)
        title('1');
    else
        title('2');
    end
end

结果如下图所示：

　　很明显，第四行的第四张图识别错误，待老衲吧k-manifolds的代码调试后对比一下效果，最后感谢谷歌搜索带来的以下资料：

http://www-clmc.usc.edu/publications/T/tenenbaum-Science2000.pdf

http://isomap.stanford.edu/

以及王勇博士的博士论文《基于流形学习的分类与聚类方法及其应用研究》