【图机器学习】cs224w Lecture 6 - 消息传递 及 节点分类
转自本人:https://blog.csdn.net/New2World/article/details/105410276
前面几课时讲的主要是图的性质、一些基本结构和针对结构的算法。而从现在开始就要涉及到具体的 learning 任务了。这一讲要解决的主要问题是:给定一个网络以及网络里一部分节点的标签,我们如何为其它节点分类。(semi-supervised)
我们使用的模型叫 collective classification model,其中有三种近似推断的方法,它们都是迭代型算法。
- relational classification
- iterative classification
- belief propagation
exact inferencevs.approximate inference
例如在一个图里每个节点都是离散的随机变量,而所有节点的类别的联合分布为 \(p\)。那么我们要得到某个节点的类别的分布就是求 \(p\) 在该节点上的边沿分布。而边沿分布需要累加其它所有节点,这个计算量爆炸,因此需要近似推断。
近似推断其实就是缩小传播范围的过程,与其考虑所有节点,我们只关心目标节点的邻接点。这里涉及到信息传递,就是类似 GNN 里的 aggregation,后面会说到。
Node Classification
给节点分类,我们的第一想法是节点间通过边的连接存在着相关性,那我们直接通过相关性对节点进行分类。关联性主要有三种
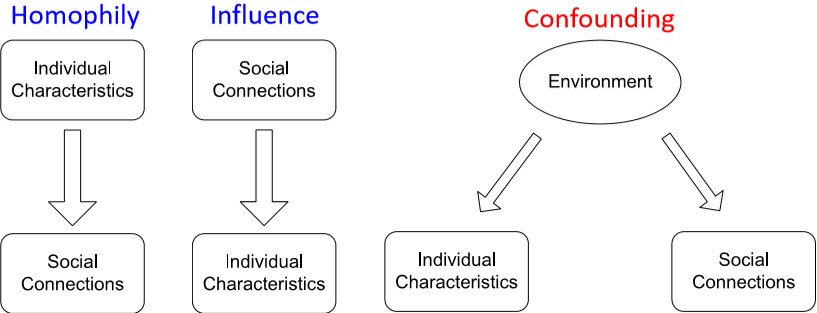
- homophily:“物以类聚,人以群分”,有相同性质的节点间可能存在更密切的联系
- influence:“近朱者赤,近墨者黑”,一个个体有可能会受其它个体的影响而具有某种性质
- confounding:大环境可能会对个体性质和个体间的联系产生影响
那么将这种关联性的特点应用在节点分类里,相似的节点间一般会有直接的联系,互相连接的点很有可能属于同一类别,这就是 guilt-by-association (关联推断)。而节点类别的判断可以基于节点的特征以及邻接节点的类别和特征。
由于做的是近似推断,所以这里需要做出马尔可夫假设,即节点 \(i\) 的类别 \(Y_i\) 只取决于它的邻接节点 \(N_i\)。因此有 \(P(Y_i|i)=P(Y_i|N_i)\)
Collective classification 大体分为三步:
- local classifier:就像一般的分类任务一样,只依赖节点自己的特征信息而不牵扯任何网络信息
- relational classifier:考虑邻接点的标签和特征
- collective inference:迭代地将 relational classifier 应用在每个节点上,相当于拓展了节点的“感知野”
Probabilistic Relational Classifier
基本思路很简单,每个节点类别的概率是其邻接节点的加权平均。
首先将有标签的点的类别初始化为标签,没有标签的点初始化为随机。然后按随机顺序进行邻接节点类别加权,直到整个网络收敛或达到最大迭代次数。但这样做有两个问题,第一不保证收敛;其次这样的模型并没有用到节点的特征。
Iterative Classification
其实就是加上节点特征后的迭代过程。(1) Bootstrap phase,通过训练集训练两个分类器,一个针对节点本身的特征,一个针对节点和网络连接特征 (数据来自其它网络),比如 SVM 什么的。然后对每个节点提取特征并用第一个分类器来初始化标签。因为分类器并没有考虑网络信息,因此还需要 (2) Iteration phase 对网络中的关联进行迭代,即使用第二个分类器每个节点根据其邻接点更新特征和标签,直到收敛或达到最大迭代次数。然而这个方法依然无法保证收敛。
slide 里给了一个用 word-bag 作为特征的网页分类的例子,感兴趣可以去看看。
接下来是一个 iterative classification 的应用,对 fake reviewer/review 进行分类。它将 reviewer 和网页作为二分图处理,虽然也可以加上 reviewer 间的关系,但那样做会破坏这个方法的两个优点:(1) 迭代次数有上界;(2) 时间复杂度和边的条数成线性。
论文里给 reviewer,review 和网页都定义了 quality score。然后大致按照上面讲的方法对这些值进行迭代更新。
- reviewer: \(F(u)=\frac{\sum\limits_{(u,p)\in Out(u)}R(u,p)}{|Out(u)|}\)
- review: \(R(u,p)=\frac1{\gamma_1+\gamma_2}(\gamma_1F(u)+\gamma_2(1-\frac{|score(u,p)-G(p)|}2))\)
- 网页: \(G(p)=\frac{\sum\limits_{(u,p)\in In(p)}R(u,p)\cdot score(u,p)}{|In(p)|}\)
有学生问到一个问题:如果一个人对所有网页都给 good review,那他算不算 fake?
Michele 的回答是这样做只会让这个人的评分趋近 \(0.5\) 而不会像那种给好网页评负分的真正的 fake reviewer 那样得分趋近 \(0\)
另一个有意思的问题是,如果某个人口味独特,给某些奇怪的网站评了高分,会不会被认为是 fake?
我很好奇口味有多独特,奇怪的网页指什么。但实际上世界很大,网络规模也很大,有独特癖好的不止你一个,因此你不孤单。总有那么一群人给这些奇怪的网页评高分,相对来说也就不会被分为 fake。不过这个问题也得看实际情况。
Belief Propagation
信念传播是一个动态规划的过程,主要用于解决图模型中的条件概率问题。不过在看它到底是什么东西前我们先了解下信息传递是怎么回事。想象一群高度近视的人不戴眼镜在操场上排了个纵队,他们只能看到前面和后面一个人。这种情况下如何让他们知道自己在第几个?很简单,第一个人告诉第二个人“你前面有一个人(就是第一个人自己)”,第二个人告诉第三个人“你前面俩人”,依次类推所有人都知道自己第几了。同理,如果从最后一个人开始往前,那么就能知道队伍的总人数了(正数和倒数第几都有了)。这个道理用到网络里其实差不多,每个节点能知道自己的大概位置。但是一旦遇到环,这个方法就没完了……这个我们待会儿再说。该介绍信念传播的算法了:Loopy Belief Propagation
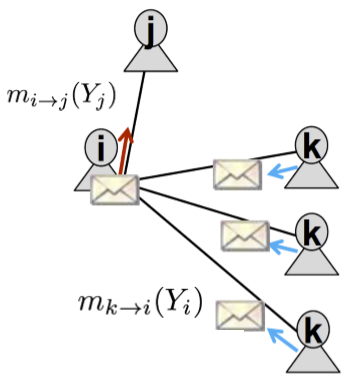
在上图的简单网络结构中,节点 \(i\) 发给 \(j\) 的信息包含了节点 \(k\) 发给 \(i\) 的信息。因此先做如下定义
- label-label potential matrix \(\psi(Y_i,Y_j)\):表示节点 \(i\) 是类别 \(Y_i\) 的条件下,其邻接节点 \(j\) 为类别 \(Y_j\) 的概率
- prior belief \(\phi_i(Y_i)\):表示节点 \(i\) 为类别 \(Y_i\) 的先验概率
- \(m_{i\rightarrow j}(Y_j)\):节点 \(i\) 在多大程度上认为其邻接节点 \(j\) 是类别 \(Y_j\) (不知道这里能不能算作是一个概率)
这个式子应该很好理解:节点 \(i\) 为 \(Y_i\) 时,有个先验 \(\phi\),同时它会收到节点 \(k\) 的信息 \(m_{k\rightarrow i}(Y_i)\),然后根据类似转移矩阵的 \(\psi\) 得到节点 \(j\)。这里的 \(\alpha\) 类似于学习率。
老规矩,随机顺序迭代,直到收敛,然后就得到了节点 \(i\) 是类别 \(Y_i\) 的信念。
好,信念传播的过程和模型介绍了,需要来解决环的问题了。在传播过程中,环的存在可能会导致信念的重复累加,但这样对结果不会造成太大影响,因为它无非就是让节点更加确信结果而已。其最主要的问题是可能会导致原本相关的信息被作为独立信息来处理,如下图中圈出的两个信息。这两条信息其实是同一条,但因为信念传播是局部算法,因此它会将这两条信息作为相互独立的两条信息来对待。那我们怎么解决呢?我没理解错的话 Michele 的意思是不用处理……因为这个例子很极端,而实际中环的影响很弱,比如有些环很~长,而大多数环存在至少一种弱相关性[1]。
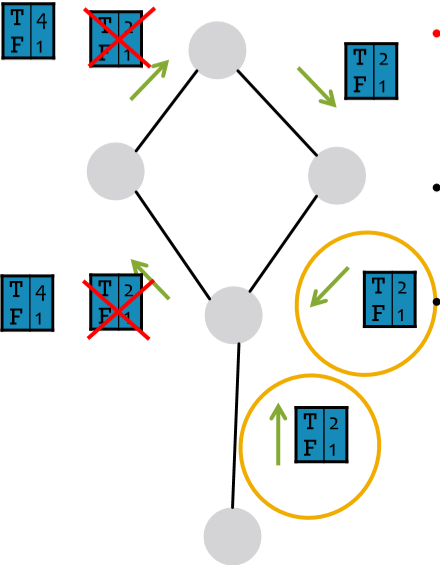
图里那两个
T4F1应该是T4F2
核心算法已经讲了,后面还举了个栗子,自己看 slide 吧。
这里的 weak correlation 不太明白是什么意思。弱相关能解环?还是说这里的 correlation 就是 link 的意思,然后 weak 代表传播的概率在这里很小? ↩︎



 浙公网安备 33010602011771号
浙公网安备 33010602011771号