【图机器学习】cs224w Lecture 4 - 社区结构
Community
转自本人:https://blog.csdn.net/New2World/article/details/105328390
之前讲到了网络中节点扮演不同角色,而角色这个概念和社区互补,那么接下来就讨论下社区这个概念。
以找工作为例,曾经学者 Granovetter 调查过人们的工作是由谁介绍的,结果很意外。大部分人的工作是由“熟人”,或者说关系并不是很密切的人介绍的。然后 Granovetter 分析后提出了他的解释:这种“熟人”可能涉及整个社交网络很广泛的区域 (普遍来说通过 \(6.6\) 个人就能认识全世界任何人)。这样一来他们很可能覆盖了很多行业,其中一个就是你的专业。然后将这个解释整理一下就得到了如下两个方面的结论:
- 结构上连接紧密的边的社会性更强;跨度大的边连接了网络不同的两个或多个领域反而社会性不稳定
- 从信息传播的角度来看,跨度大的边能传递不同领域的信息,在找工作方面更有利;而结构上连接密的边过于冗余因此无法提供新的信息
Granovetter 的这个理论在后来电话网络中得到了印证,即连接更强的边一般都有更频繁的电话联络。这里提到一个 edge overlap 需要记录一下,它衡量了两个点间连接的紧密程度。当某条边是 local bridge 时,重叠率为 \(0\)。
那如果我们按重叠率从小到大来移除边,那整个网络会很快变成不相连的几个部分,也就是说网络的最大相连的部分大小会很快缩小。如此一来我们就可以断定这个网络里存在不同的社区。那么给出社区的定义:包含大量内部连接和少量外部连接的节点集合。一个比较经典的社团网络是 Zachary 的 Karate club network
给出具有明显社区的网络的邻接矩阵,按一定顺序排列节点可以明显看出有分块的趋势。
按套路来说,这时候应该要提出一个用来衡量网络是否具有典型的社区的标准了。那么他来了:modularity \(Q\)。给定网络中的一些点作为一个划分 \(s\in S\)
这个式子的结果衡量的是:到底图里的边或边的权重比我们预想的多多少?如果多很多那说明存在一个社区,少很多说明是 bridge。那这里的 expected 是怎么来的呢?再一次请出零模型
Configuration Model
现在我们的目标是给定 \(n\) 个节点 \(m\) 条边,然后生成一个具有相同度分布的随机网络。不同于之前我们构建的零模型,这里我们只需要知道节点间边的期望,或者对于无向图来说就是有边的概率。这里可以通过每个节点的度来计算节点间边的期望 \(p(i,j)=k_i\frac{k_j}{2m}\)
那么这个图里所有边的期望为
\[\begin{aligned}E_{edge}&=\frac12\sum_{i\in N}\sum_{j\in N}\frac{k_ik_j}{2m} \\ &=\frac12\frac1{2m}\sum_{i\in N}k_i(\sum_{j\in N}k_j) \\ &=m\end{aligned} \]
有了这个期望后,我们将 modularity 这个概念具体化。其中 \(\delta\) 是判别函数,判断两个节点所属社区是否相同,即只考虑划分 \(s\) 内的所有边。
得到的 \(Q\) 值落在 \([-1,1]\),正值表示图中的边多余预期。一般地,\(Q\) 大于 \(0.3\) ~ \(0.7\) 表明图中存在明显的社区结构。
Louvain Algorithm
根据上面推导到的 modularity 我们可以想到将 \(Q\) 最大化就能得到一个比较好的划分方案。于是 Louvain 算法就是基于这样思想的一个贪心算法。而且它具有
- 速度快
- 收敛快
- 结果好
- 支持嵌套社区结构
这个算法分两步,然后不停迭代直到收敛
- 在局部范围内交换节点的社区,如果交换后能使 modularity 增大则保留交换,否则回退
- 在第一步收敛后将所有属于同一社区的节点汇聚为一个超级节点,然后根据原图结构连接这些超级节点形成新的图,而边的权重是所有对应边的权重之和
在第一步里还有很多细节。初始化的时候给所有节点分配一个单独的社区。交换社区怎么做呢?将节点 \(i\) 的社区改变为其任一邻接节点 \(j\) 的社区,然后计算 \(\Delta Q\),在得到所有邻接节点的 \(\Delta Q\) 后取其中最大的。这里有学生问节点遍历顺序的问题,的确,遍历顺序会影响最终结果。但 Jure 在 slide 里批注到根据研究表明节点顺序并不会对结果产生很大影响,因此无所谓。
那么现在还有一个问题,就是这个 \(\Delta Q\)。虽然说这是 modularity 的变化量,但思考一下,改变一个节点的社区类型其实是两步操作:首先将这个节点从原社区移除,然后才能将其加入新的社区。那这里的 \(\Delta Q\) 就需要包括移除和加入两步对 modularity 的影响。因此定义 \(\Delta Q(i\rightarrow C)\) 将节点 \(i\) 加入社区 \(C\);\(\Delta Q(D\rightarrow i)\) 将节点 \(i\) 从社区 \(D\) 移除。\(\Delta Q=\Delta Q(i\rightarrow C)+\Delta Q(D\rightarrow i)\)。其中移除节点的具体表达为
- \(\sum_{in}\) 社区 \(C\) 内边的权重之和
- \(\sum_{tot}\) 与社区 \(C\) 内所有点相连的边的权重
- \(k_{i,in}\) 节点 \(i\) 和社区 \(C\) 内所有点的连接的权重和
- \(k_i\) 与节点 \(i\) 连接的所有边的权重和
(目前先理解加入这一步,但没有自己推导;而移除的表达式没有推,后面有时间会补上)
下图是这个计算式的 intuition [1]
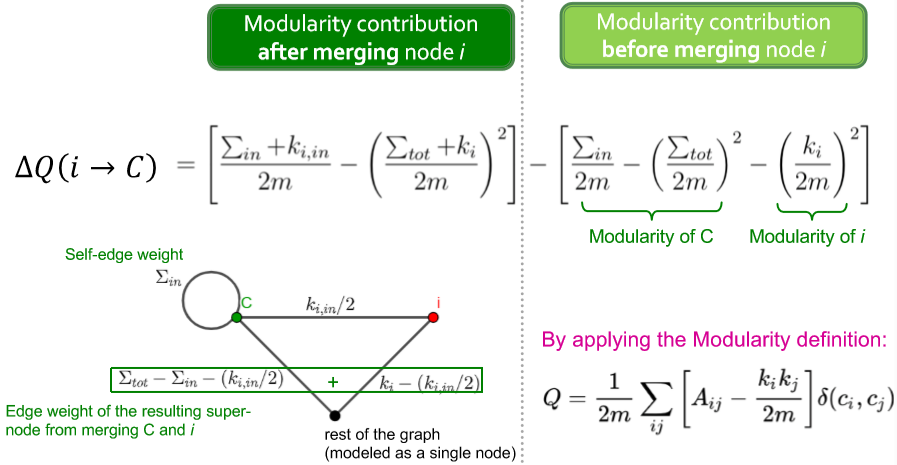
具体伪码有点长就不贴了,但需要说明一点。在移动了节点的社区类型后社区结构变了,看起来需要重新数边什么的,然而可以根据改变了的节点的信息更新社区信息,因此只是简单的加减法而不需要重新数。
这里学生提到一个问题,就是什么时候结束算法?这里我们其实不需要手动中止,因为 Louvain 保证收敛,所以只要让它跑完就行。每迭代一次都会输出一次 modularity,而我们只需要取 modularity 最大的那一次迭代就能确定多少社区合适,并从而获取社区的聚类。一般来说算法最后都会收敛到剩下两个社区。
另一个学生提问:这个算法在多大程度上收敛到最优解。这个问题 Jure 的回答是不知道,但应该不差。
BigCLAM
Louvain 虽然好处多多应用也广,但有个缺陷,它只能给每个节点分配一个社区。然而现在社会结构复杂,一个人可能参加多个社团或属于多个社区,这样就是 overlap 的问题。用邻接矩阵来表示更直观
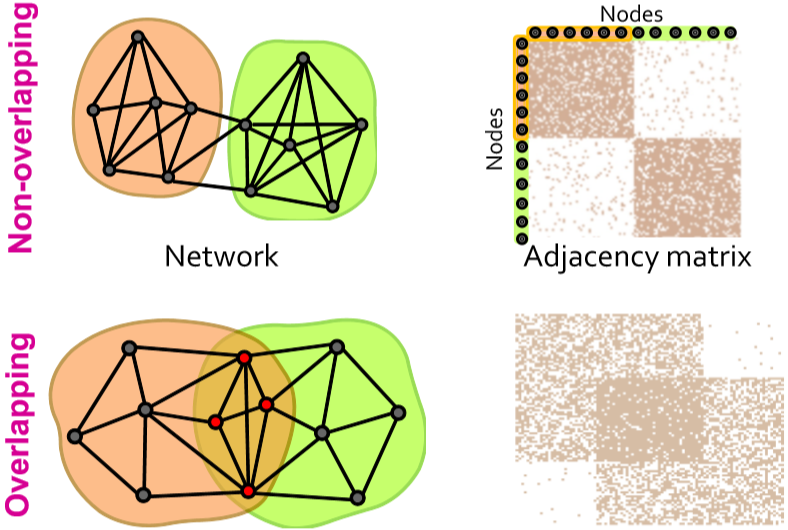
这里采取的思路是:首先设计一个能生成重叠图的模型,然后通过调整模型参数来拟合给定的图。这个模型叫 Community Affiliation Graph Model (AGM),它的定义很直观。给定社区集合 \(C\),节点集合 \(V\) 以及成员关系 \(M\) 表示某个节点属于某个或多个社区。社区 \(c\) 内部的点互相连接的概率为 \(p_c\),那么任意两个节点互相连接的概率就是 \(p(\mu,\nu)=1-\prod\limits_{c\in M_{\mu}\cap M_{\nu}}(1-p_c)\)。AGM 不仅能表示重叠,还能表示嵌套的情况,因此是个很有效的模型。而现在我们要做的就是通过给定的网络结构反推 AGM 模型,包括社区个数、节点与社区的隶属关系以及每个社区内的连接概率。即给定图 \(G\),找模型 \(F\),相当于最大化概率 \(P(G|F)=\prod\limits_{(\mu,\nu)\in G}P(\mu,\nu)\prod\limits_{(\mu,\nu)\notin G}(1-P(\mu,\nu))\)
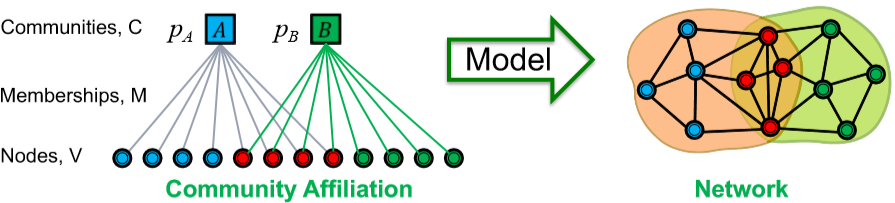
但是这种“有就是有,没有就是没有”的定义太死板了,需要松弛一下。所以给每个节点定义一个向量 \(F_{\mu}\) 表示这个节点属于各个社区的权重(或概率)。这样就需要调整节点间连接的概率 \(P(\mu,\nu)=1-\exp(-F_{\mu}F_{\nu}^T)\),而我们需要最大化的目标就是这样的一个似然函数
那接下来需要做的就是
- 随机初始化 AGM 的参数 \(F\)
- 固定其他节点的社区成员关系,更新节点 \(\mu\)
至于怎么做 Jure 这里因为快下课了就没讲。但是提点了一下,就是大家再熟悉不过的梯度上升了。这里梯度为
这里看起来是要对所有非邻节点的 \(F_{\nu}\) 求和,但实际上只需要保存然后随迭代更新就行了。因此这一步的复杂度是和节点的度呈线性关系的。
这里 \(i\) 到 \(C\) 的权重为什么是 \(k_{i,in}/2\),不应该就是 \(k_{i,in}\) 吗? ↩︎




 浙公网安备 33010602011771号
浙公网安备 33010602011771号