CF1221F Choose a Square

题目链接

博客食用更佳哦

蒟蒻真的是菜啦，花一天时间才过这道题。

如果您是巨佬，还请移步至楼上@jun头吉吉的题解。

题目大意

有 \(n\) 个点求构造一个内部点权（包含边界）减去边长最大的，对角线在 \(y=x\) 上的正方形。输出内部点权减去边长的值，以及正方形左下角和右上角的坐标。

核心思路

正方形需要考虑直线 \(y=x\) 两边的操作，方便起见，根据正方形的对称性，我们直接把在直线下方的点关于直线对称到直线上方（将横纵坐标交换即可），那么这道题就变成了求一个等腰直角三角形。

考虑到如果三角形的边界上没有点的话，相当于在一个边界有点的三角形的基础上进行扩大，边权变大，显然较劣，所以每次都考虑边上有点的情况。

由于边都是平行于 \(x\) 轴和 \(y\) 轴的，所以我们想到用线段树家扫描线的方法求解。

具体操作

我们按照 \(y\) 为第一关键字从小到大排序。

对 \(x\) 和 \(y\) 分别进行离散操作，以离散后的 \(x\) 序列的下标为叶子节点建立线段树。

接下来考虑两种操作：

1. 在当前扫描线上加点。

对于这种情况，由于新加点只会被三角形顶点的 \(x\) 坐标更小的包含，所以我们进行区间加，从 \(1\) 到 \(idx\) 加 \(w\)。（\(idx\) 表示离散后的位置）

2. 扫描线上移，并新加点。

这种情况就比较麻烦了。

• 由于上一条线已经处理完了，所以我们要对其询问取 \(\max\) ，取从 \(1\) 到 \(x\) 的最大值。

• 扫描线上移，意味着每一个 \(x\) 上建立三角形的边长会增加，我们分两部分处理，一部分是上一次线上包含的 \(x\) ,另一部分是新加的 \(x\) ,分别为图中标蓝和标红的区域。蓝色区间加，红色暴力枚举修改。

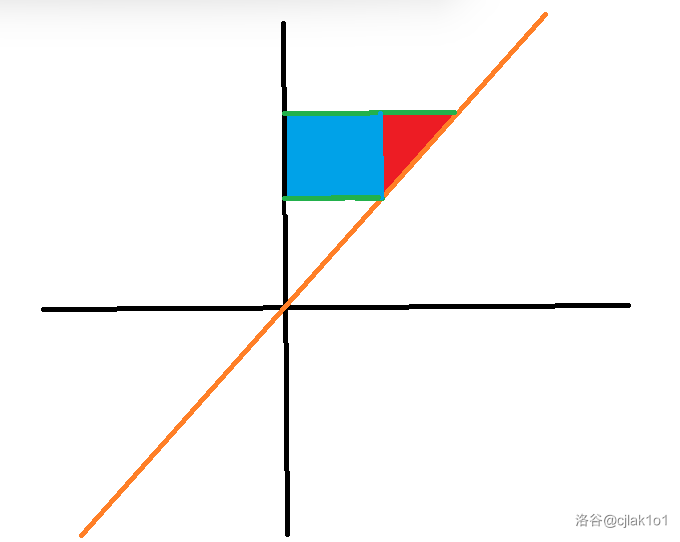
还要记得预处理第一根扫描线。

code

#include<bits/stdc++.h>
#define int long long
#define mp make_pair
#define fi first
#define se second
#define ls rt<<1
#define rs rt<<1|1
#define lson ls,l,mid
#define rson rs,mid+1,r
using namespace std;
const int N=5e5+1e4,Inf=1e15+7;

int read(){
	int res=0,f=1;char c;
	for(;!isdigit(c);c=getchar()) if(c=='-') f=-1;
	for(;isdigit(c);c=getchar()) res=(res<<1)+(res<<3)+(c^48);
	return res*f;
}

int n,Px[N],cntx,Py[N],cnty,last=-1;
struct node{
	int x,y,w;
	bool operator < (const node &b)const{return y==b.y?x<b.x:y<b.y;}
}a[N];

struct TREE{
	int sum,id,lazy;
}t[N<<2];
void push_up(int rt){
	t[rt].sum=max(t[ls].sum,t[rs].sum);
	t[rt].id=t[ls].sum>t[rs].sum?t[ls].id:t[rs].id;
}
void push_down(int rt,int l,int r){
	if(t[rt].lazy){
		int k=t[rt].lazy,mid=(l+r)>>1,Len=mid-l+1,Ren=r-mid;
		t[ls].sum+=k,t[rs].sum+=k,t[ls].lazy+=k,t[rs].lazy+=k,t[rt].lazy=0; 
	}
}
void build(int rt,int l,int r){
	if(l==r) return t[rt].id=l,void();
	int mid=(l+r)>>1;build(lson),build(rson),push_up(rt);
}
void update(int rt,int l,int r,int ul,int ur,int k){
	if(ul<=l&&r<=ur) return t[rt].sum+=k,t[rt].lazy+=k,void();
	push_down(rt,l,r);int mid=(l+r)>>1;
	if(ul<=mid) update(lson,ul,ur,k);
	if(mid<ur) update(rson,ul,ur,k);
	push_up(rt);
}
void update(int rt,int l,int r,int ul,int ur){
	
}
pair<int,int> query(int rt,int l,int r,int ql,int qr){
	if(ql>r||l>qr) return mp(0ll,-1ll);
	if(ql<=l&&r<=qr) return mp(t[rt].sum,t[rt].id);
	int mid=(l+r)>>1;
	return max(query(lson,ql,qr),query(rson,ql,qr));
}

pair<int,int> ans;
int upup;

signed main(){
	n=read();upup=500000,ans.se=500000;
	for(int i=1;i<=n;i++){
		a[i].x=read(),a[i].y=read(),a[i].w=read();
		if(a[i].x>a[i].y) swap(a[i].x,a[i].y);
		Px[++cntx]=a[i].x;Py[++cnty]=a[i].y;
	}
	sort(a+1,a+n+1);sort(Px+1,Px+n+1);sort(Py+1,Py+n+1);
	cntx=unique(Px+1,Px+n+1)-Px-1;
	cnty=unique(Py+1,Py+n+1)-Py-1;
	build(1,1,cntx);//以离散后的x为叶子节点建树 
	int ur1=upper_bound(Px+1,Px+cntx+1,a[1].y)-Px-1;
	for(int i=1;i<=ur1;i++) update(1,1,cntx,i,i,Px[i]-a[1].y);
	int idx,_idx,idy,_idy;
	for(int i=1;i<=n+1;i++){
		if(i<=n) idx=lower_bound(Px+1,Px+cntx+1,a[i].x)-Px,idy=lower_bound(Py+1,Py+cnty+1,a[i].y)-Py;
		if((i!=1&&idy!=_idy)||i==n+1){//扫描线上移
			last=a[i-1].y;
			pair<int,int> sum=query(1,1,cntx,1,_idx);
			if(sum.fi>ans.fi) ans.fi=sum.fi,ans.se=Px[sum.se],upup=a[i-1].y;
			if(i==n+1) break;
			int ur=upper_bound(Px+1,Px+cntx+1,a[i-1].y)-Px-1,uR=upper_bound(Px+1,Px+cntx+1,a[i].y)-Px-1;
			//ur,uR分别表示两条线上最靠右的存在的x
			update(1,1,cntx,1,ur,a[i-1].y-a[i].y);//蓝色部分
			for(int j=ur+1;j<=uR;j++) update(1,1,cntx,j,j,Px[j]-a[i].y);//红色部分
		}
		if(i<=n) update(1,1,cntx,1,idx,a[i].w);
		_idx=idx,_idy=idy;
	}
	printf("%lld\n%lld %lld %lld %lld\n",ans.fi,ans.se,ans.se,upup,upup);
	return 0;
}
/*
7
5461255 4302067 16
1325913 2652299 15
1735 2640383 11
5293204 2140683 29
3729701 5526121 14
2769558 6182111 22
4396749 3148205 17
*/