BUAA_OO_Unit1总结
Unit1 总结
1. 程序结构分析
1.1 代码结构(类图)
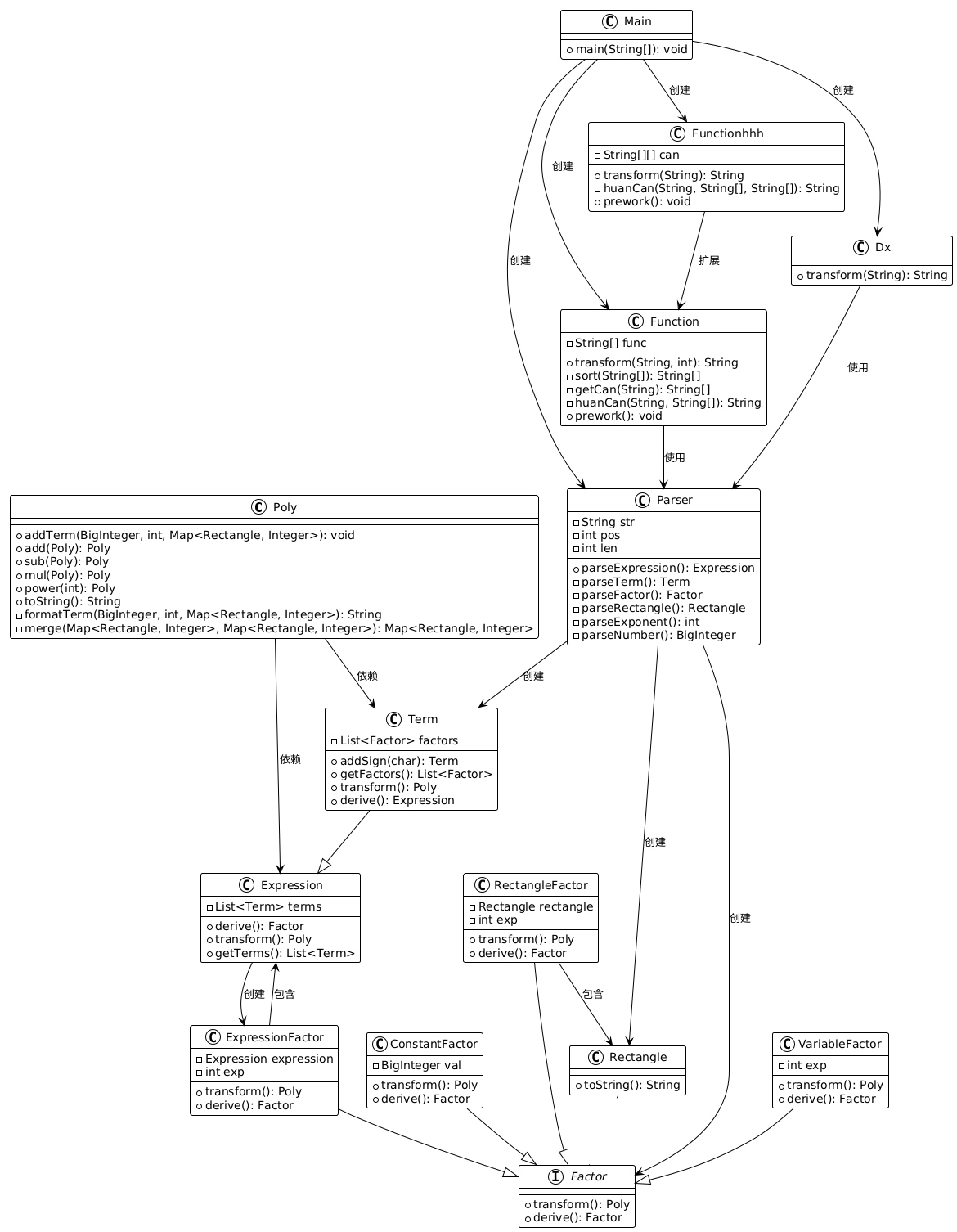
1.2 类的度量统计
| 类名 | 属性个数 | 方法个数 | 方法名 | 方法规模(代码行) | 控制分支数目 | 类总代码规模(行) |
|---|---|---|---|---|---|---|
| Function | 4 | 6 | Function |
5 | 0 | 85 |
sort |
10 | 1 (双重循环) | ||||
getCan |
20 | 3 (条件+循环嵌套) | ||||
huanCan |
15 | 2 (条件替换逻辑) | ||||
prework |
15 | 2 (条件+循环) | ||||
transform |
30 | 5 (循环+递归解析) | ||||
| Main | 0 | 1 | main |
10 | 0 | 10 |
| ExpressionFactor | 2 | 2 | transform |
10 | 1 (条件) | 20 |
derive |
12 | 2 (循环+条件) | ||||
| Dx | 0 | 2 | Dx |
1 | 0 | 25 |
transform |
20 | 4 (循环+嵌套解析) | ||||
| Factor | 0 | 2 | transform (接口) |
0 | 0 | 4 |
derive (接口) |
0 | 0 | ||||
| Functionhhh | 4 | 5 | Functionhhh |
5 | 0 | 60 |
getCan |
15 | 3 (条件+循环嵌套) | ||||
huanCan |
20 | 2 (参数替换逻辑) | ||||
prework |
10 | 1 (循环) | ||||
transform |
30 | 4 (循环嵌套替换) | ||||
| Parser | 3 | 8 | Parser |
10 | 1 (符号处理) | 110 |
parseExpression |
20 | 2 (符号递归解析) | ||||
parseTerm |
15 | 3 (因子组合解析) | ||||
parseFactor |
40 | 6 (多重分支解析) | ||||
parseRectangle |
10 | 1 (条件解析) | ||||
parseExponent |
8 | 1 (条件) | ||||
parseNumber |
10 | 2 (符号+数字解析) | ||||
| Poly | 1 | 9 | addTerm |
10 | 2 (Map合并逻辑) | 130 |
add |
15 | 2 (循环合并项) | ||||
sub |
15 | 2 (循环项取反) | ||||
mul |
30 | 3 (双重循环乘法) | ||||
merge |
10 | 2 (Map合并) | ||||
power |
25 | 4 (位运算+循环) | ||||
toString |
35 | 6 (多项条件格式化) | ||||
formatTerm |
30 | 5 (符号和幂次处理) | ||||
| ConstantFactor | 1 | 2 | transform |
8 | 0 | 12 |
derive |
3 | 0 | ||||
| Expression | 1 | 4 | derive |
15 | 2 (循环项派生) | 25 |
transform |
8 | 1 (循环合并项) | ||||
getTerms |
1 | 0 | ||||
| Rectangle | 2 | 2 | toString |
10 | 1 (条件判断表达式复杂度) | 25 |
derive |
15 | 2 (type类型判断+因子组合) |
||||
| RectangleFactor | 2 | 4 | transform |
8 | 0 | 35 |
derive |
12 | 1 (递归调用条件) | ||||
same |
3 | 0 | ||||
merge |
2 | 0 | ||||
| Term | 1 | 4 | addSign |
5 | 1 (sign符号判断) |
30 |
transform |
10 | 1 (循环乘法操作) | ||||
derive |
15 | 2 (循环遍历因子+条件分支) | ||||
getFactors |
1 | 0 | ||||
| VariableFactor | 1 | 2 | transform |
6 | 0 | 20 |
derive |
10 | 1 (exp == 0条件判断) |
1.3 分析与自我评价
1.3.1 内聚性、耦合性分析
高内聚类
Poly类- 优点:专注于多项式的存储和运算(加、减、乘、幂次、合并项等),所有方法围绕多项式操作展开,职责单一。
- 示例:
add()、mul()等方法仅处理多项式运算逻辑,无其他无关功能。
ConstantFactor类- 优点:仅实现常数因子的转换和求导逻辑,代码简洁且高度聚焦。
VariableFactor类- 优点:专注于变量因子(如
x^exp)的转换和求导,逻辑清晰。
- 优点:专注于变量因子(如
低内聚类
Function和Functionhhh类- 问题:两者功能高度相似(处理函数替换和参数解析),但未通过继承或组合复用代码,导致职责分散。
- 示例:
getCan()和huanCan()方法在两个类中重复实现,违反单一职责原则。
Rectangle类- 问题:同时承担几何表示(如
sin/cos)和代数运算的职责,混合了领域逻辑。 - 示例:
derive()方法包含三角函数求导逻辑,与代数表达式解析无关。
- 问题:同时承担几何表示(如
低耦合模块
Factor接口及其实现类- 优点:通过接口抽象,
Expression和Parser仅依赖Factor接口,而非具体实现类,符合依赖倒置原则。
- 优点:通过接口抽象,
Parser类- 优点:通过
parseFactor()动态创建Factor对象,减少对具体类的直接依赖。
- 优点:通过
高耦合模块
Function与Functionhhh类- 问题:两者直接依赖相同的字符串替换逻辑,且未通过抽象隔离,导致修改一处可能影响另一处。
Poly与Term类- 问题:
Poly直接操作Term的因子列表,未通过接口隔离,导致Poly需要了解Term的内部结构。
- 问题:
Rectangle与ExpressionFactor类- 问题:
Rectangle的derive()方法直接创建ExpressionFactor对象,形成紧耦合。
- 问题:
1.3.2 代码优缺点总结
优点:
- 模块化设计
Factor接口和Poly类的设计体现了职责分离,便于扩展新因子类型或运算逻辑。
- 接口抽象
Factor接口统一了因子转换和求导行为,支持多态调用。
- 递归解析能力
Parser类的递归下降解析方法(如parseExpression())灵活处理复杂表达式。
缺点:
- 重复逻辑
Function和Functionhhh类中的getCan()和huanCan()方法重复实现。
- 紧耦合设计
Rectangle类直接依赖ExpressionFactor,导致几何逻辑与代数逻辑混杂。
- 冗余分支判断
Parser.parseFactor()和Poly.formatTerm()包含过多条件分支,增加维护成本。
- 缺乏封装
Term类的factors列表直接暴露给外部(如getFactors()),违反封装原则。
1.3.3 改进方法
1. 内聚性优化
- 合并重复功能
- 将
Function和Functionhhh合并为FunctionHandler类,通过策略模式区分不同参数替换逻辑。
- 将
- 拆分混合职责
- 将
Rectangle的几何逻辑(如sin/cos)分离到TrigonometricFactor类,保留Rectangle仅表示代数变量。
- 将
2. 耦合性优化
- 依赖抽象而非实现
Poly类应依赖Term的接口(如TermInterface),而非直接操作其内部factors列表。Rectangle.derive()应返回Factor接口对象,而非具体ExpressionFactor。
3. 代码复用与简化
- 提取工具类
- 将
Function和Functionhhh的公共逻辑(如字符串替换)封装到StringUtils工具类。
- 将
- 使用模板方法模式
- 在
Parser类中统一处理符号解析逻辑,减少parseFactor()的条件分支。
- 在
4. 增强封装性
- 隐藏内部状态
- 移除
Term.getFactors()方法,改为通过Term内部方法操作因子列表。 - 将
Poly.terms的访问权限设为private,通过方法提供安全访问。
- 移除
实例:
// 改进1:合并 Function 和 Functionhhh
public class FunctionHandler {
private FunctionType type; // 枚举区分不同函数类型
public FunctionHandler(FunctionType type) { /* ... */ }
public String transform(String input) { /* 根据类型调用不同替换逻辑 */ }
}
// 改进2:拆分 Rectangle 的几何逻辑
public class TrigonometricFactor implements Factor {
private String type; // "sin" 或 "cos"
private Factor inner;
@Override
public Factor derive() {
// 实现三角函数求导逻辑,不依赖 ExpressionFator
}
}
2. 架构设计体验
第一单元的作业针对“表达式展开”问题进行了三次开发。
第一次作业主要考察递归下降在解析表达式中的应用。由于不涉及复杂的运算,加上有先导课程的基础,本次作业比较容易完成。只要按照递归下降的方法逐层解析表达式、因子、项,并依次展开即可。
第二次作业加入了递推函数表达式和三角函数。对于递推函数,我在进行递归下降前添加了解析函数的部分,也就是先把所有 \(f\) 都替换成普通的表达式,然后再进入第一次作业的流程。这样只需要加入一个预处理步骤,不需要对第一次作业进行任何修改。对于三角函数,添加 \(\text{Rectangle}\) 类,包含函数类型及内部因子,其余操作和幂因子、表达式因子差不多。
第三次作业加入求导和普通函数。普通函数的部分很好处理。对于求导,再次添加一步预处理操作:将所有dx替换为普通表达式。在执行这一步时,为了方便且避免错误,我对dx内的表达式执行递归下降的解析并求导。需要注意的是,最好先预处理函数,再预处理dx。
在迭代开发、设计的过程中,我对这一问题的理解越来越深刻,对于java代码结构的掌控能力也一步步提升。
3. bug分析
第二次作业的提交在出现连续四个正负号时会出错。为了避免类似的情况,我增添了一步预处理:将所有连续的一段正负号缩写为一个,避免了不必要的麻烦。
第三次作业中,我在替换dx的时候没有添加括号,导致当dx的求导内容不止一项时运算顺序错误。
除此之外,替换函数内容需要获取实参和形参,在解析双参数的函数需要找到正确的分界 \(\text{','}\),可以利用括号匹配的方法判断。
4. 优化
在处理递推函数时,我先依次处理出了 \(f_1,f_2,f_3,f_4,f_5\) 的实际表达式,避免了每次都一步步递归造成的浪费。
在答案长度上并没有做太多优化,只是简单地合并同类项。在合并自定义的类时,判断是否相同需要自己编写相应的 \(\text{equal}\) 函数。
5. 心得体会
在复杂的、拓展的任务中,一个好的基本架构非常重要,它决定了未来代码编写的难度和准确度。因此在最初设计时,要充分考虑框架的适用性和可拓展性,当架构不足以满足后续的要求时要及时修改、重构。
进行迭代开发需要我们仔细思考如何加入新功能,最好能够保持原有部分不变,减少工作量和出错的概率。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号