线性回归的变种--岭回归与Lasso回归
1.线性回归的一般形式
2.一般线性回归出现的问题及解决方法
2.1问题
2.2解决方法
3.正则化
4.岭回归与Lasso回归
4.1岭回归与lasso回归的异同
1.线性回归的一般形式
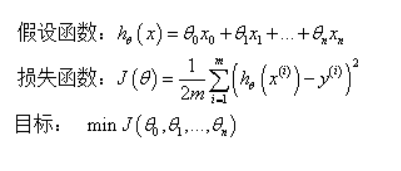
2.一般线性回归出现的过拟合问题及解决方法
2.1过拟合问题
数据少特征多容易发生过拟合问题
- 在统计学和机器学习中,overfitting一般在描述统计学模型随机误差或噪音时用到。它通常发生在模型过于复杂的情况下,如参数过多等。overfitting会使得模型的预测性能变弱,并且增加数据的波动性。
- Overfitting的概念在机器学习中很重要。通常一个学习算法是借由训练样本来训练的,在训练时会伴随着训练误差training error。当把该模型用到未知数据的测试时,就会相应的带来一个validation error。下面通过训练误差和验证误差来详细分析一下overfitting。如下图:
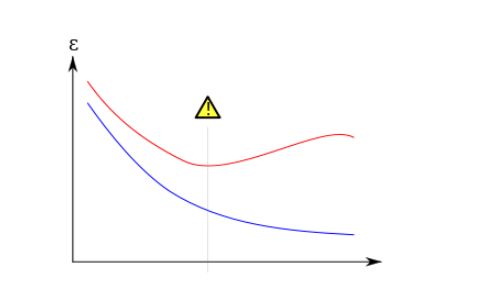
在上图中,蓝色表示训练误差training error,红色表示validation error。当训练误差达到中间的那条垂直线的点时,模型应该是最优的,如果继续减少模型的训练误差,这时就会发生过拟合。
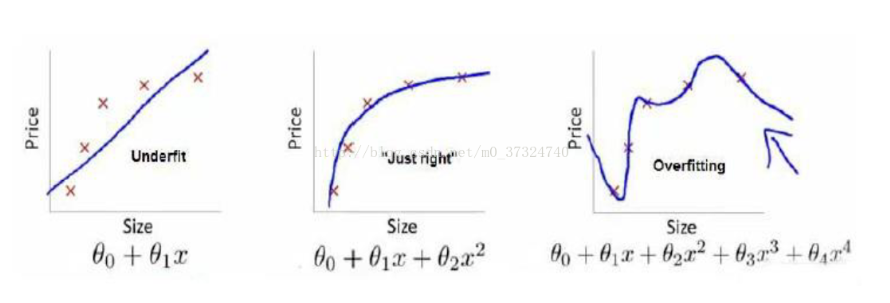
第一个模型欠拟合,第二个模型刚好拟合,第三个过拟合。
2.2解决方法
- 丢弃一些对我们最终预测结果影响不大的特征,具体哪些特征需要丢弃可以通过PCA算法来实现;
- 使用正则化技术,保留所有特征,但是减少特征前面的参数θ的大小,具体就是修改线性回归中的损失函数形式即可,岭回归以及Lasso回归就是这么做的。
3.正则化
3.1为何引入正则化(正则化的基本思想)(引用这位大神的文章)
, 其中,r(d)可以理解为有d的参数进行约束,或者 D 向量有d个维度
咱们可以令: f() =
.
- 如何去防止过拟合
显而易见,我们应该、而且只能去看【过拟合】的f(x)形式吧?
显而易见,我们从【过拟合】的图形可以看出f(x)的涉及到的特征项一定很多吧,即
显而易见,N很大的时候,
显而易见,w系数都是学习来的吧?

3.2线性回归的正则化

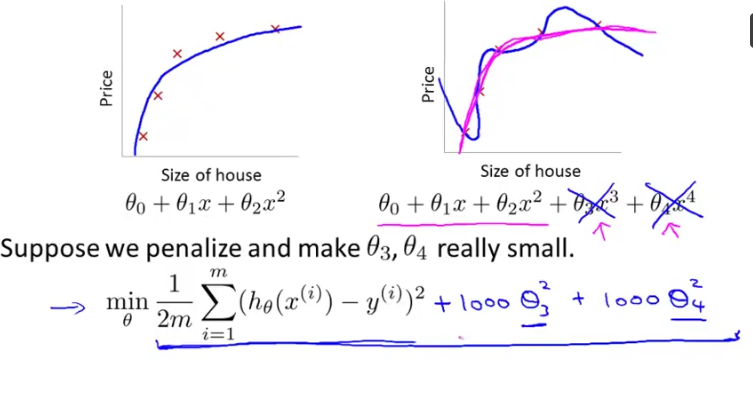
此图中![]() 即为r(d)。如果增加的式子不能让整体变小,那么只会变大。而目标是整体最小化,所以应该保证局部r(d)也应该最小化,所以
即为r(d)。如果增加的式子不能让整体变小,那么只会变大。而目标是整体最小化,所以应该保证局部r(d)也应该最小化,所以![]() 接近为0,参数取到最小。
接近为0,参数取到最小。

3.3正则化后用两种方法求解参数
梯度下降算法求解参数:(引用)

使用正规方程算法求解参数:

4.岭回归与Lasso回归
4.1岭回归与lasso回归的异同
同:
岭回归与Lasso回归的出现是为了解决线性回归出现的过拟合以及在通过正规方程方法求解θ的过程中出现的x转置乘以x不可逆这两类问题的,这两种回归均通过在损失函数中引入正则化项来达到目的,具体三者的损失函数对比见下图:
其中λ称为正则化参数,如果λ选取过大,会把所有参数θ均最小化,造成欠拟合,如果λ选取过小,会导致对过拟合问题解决不当,因此λ的选取是一个技术活。
异:
- 岭回归与Lasso回归最大的区别在于岭回归引入的是L2范数惩罚项,Lasso回归引入的是L1范数惩罚项,Lasso回归能够使得损失函数中的许多θ均变成0,这点要优于岭回归,因为岭回归是要所有的θ均存在的,这样计算量Lasso回归将远远小于岭回归。
- 从贝叶斯角度看,lasso(L1 正则)等价于参数 ww 的先验概率分布满足拉普拉斯分布,而 ridge(L2 正则)等价于参数 ww 的先验概率分布满足高斯分布。
引用文章:
https://blog.csdn.net/hzw19920329/article/details/77200475
https://www.cnblogs.com/wuliytTaotao/p/10837533.html

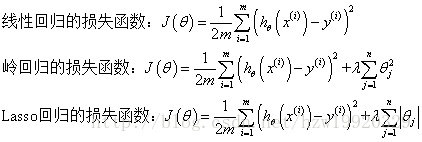

 浙公网安备 33010602011771号
浙公网安备 33010602011771号