（图论进阶笔记）【连通性】

【连通性】

图的基本概念

图论基本定理

对于任何无向图\(G = (V, E)\)，有\(\sum_{v \in V} d(v) = 2|E|\)（度数为边数的两倍）。
推论：在任意图中，度数为奇数的点必然有偶数个。

连通分量：无向图

对于一个不连通的无向图，它会被分割成多个极大连通子图，每个这样的子图称为一个连通分量
eg

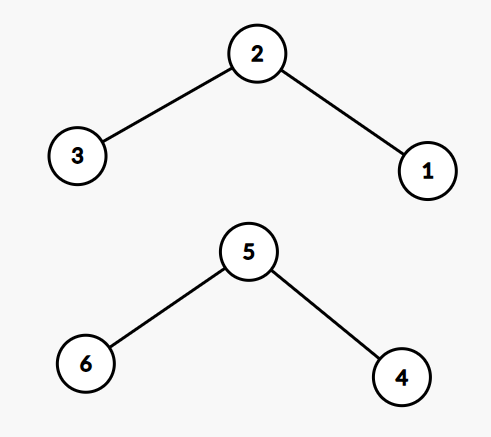
[1-2-3] [4-5-6]是连通分量
※[1-2]不是 要加一个3才是

强联通分量：有向图

有向子图的节点两两互相可达

割点/点割集

一般对于无向图
若删除某点后，图不再连通（任意两点不互达）->这样的点是割点

【性质】
从1~n一定要经过的点

割边/桥

与割点求法十分类似，都是Tarjan
若删除某边后，图不再连通（任意两点不互达）->这样的边是割边

【性质】
从1~n一定要经过的边

点连通度

最少需要删除的顶点数，使得图不再连通

边连通度

最少需要删除的边数，使得图不再连通

Whitney 定理

对任意的图\(G\)，有\(\kappa(G) \leq \lambda(G) \leq \delta(G)\)
点连通度\(\leq\)边连通度\(\leq\)最小度

点双连通VBCC

没有割点的图

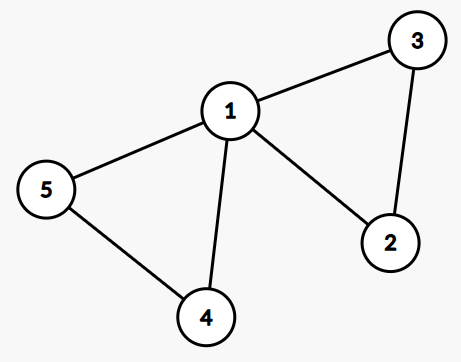
1为割点
\([1-4-5]、[1-2-3]\)为点双连通分量

边双连通EBCC

没有桥的图

\([2-5]、[2-6]\)是桥
若分\([2-5]\)：\([1-4-2-3]、[5-6]\)是边双连通分量

稀疏图/稠密图

比较边数和点数的平方

【DAG】有向无环图

【性质】
（1）可拓扑排序
（2）可DP求最短路，复杂度可降至\(O(n+m)\)

无向连通图

不含环：树
包含恰好一个环：基环树

二分图

一张图的点集可以被分为两部分，每一部分的内部都没有连边

特殊点集/边集

支配集：选择一个点/边集合，满足所有点要么在该集合内，要么与该集合内的点为邻居

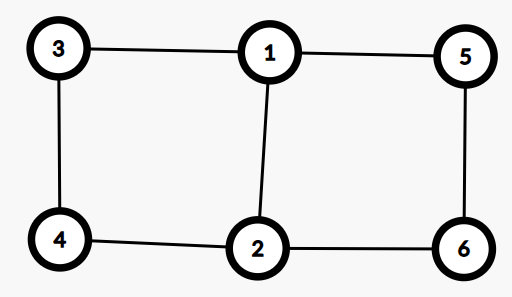
\([1-2]、[1]、[1-2-3]\)都是支配集

独立集：选择一个点/边集合，满足集合内该点互不相邻

\([1-4-6]\)是独立集

匹配：从图中选取一组边，使得这些边中的任意两条边没有公共的顶点

点覆盖：一个点集，使得每条边至少有一个端点属于该集合

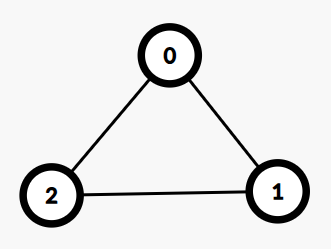
\([0,1]\)是一个点覆盖

边覆盖：一个边集，使得每个顶点都被至少一条边触及

\([\{0-1\} ,\{2-1\}]\)是一个边覆盖

团：（无向图）顶点之间完全相连的子图

竞赛图：（有向图）对于任意两个不同的顶点，恰好存在一条有向边

【性质】
(1)\(n\)个顶点的竞赛图有 \(\frac{n(n-1)}{2}\) 条有向边
(2)任意\(n≥1\)的竞赛图都存在哈密顿路径(经过所有顶点恰好一次的有向路径)
(3)图中存在King：可以击败其他所有点

【SCC】强连通分量

模版代码

实现过程

Tarjan算法