【差分约束】

【差分约束】

概念

题目会显性或隐性的给出一组约束条件(不等关系)
->转化为差分约束来解决
形如

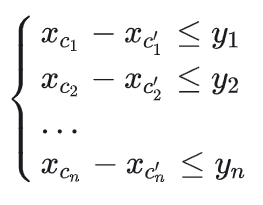
求其中x[1],x[2],...x[n]的任意解/要么无解
->最大解、最小解问题

求解逻辑

Bellman-Ford算法/SPFA算法

总结

(见https://www.zybuluo.com/DATASOURCE/note/164437)

（1）难点在于建图
（2）求解步骤：
①a-b<=c:
建一条b到a的权值为c的边
求的是最短路，得到的是最大值
②a-b>=c:
建一条b到a的权值为c的边
求的是最长路，得到的是最小值
③存在负环的话无解
④求不出最短路（dist[ ]没有得到更新）的话是任意解
（3）一种建图方法：
设x[i]是第i位置（或时刻）的值（跟所求值的属性一样）
那么把x[i]看成数列，前n项和为s[n]
则x[i]=s[i]-s[i-1]；
那么这样就可以最起码建立起类似这样的一个关系 0<=s[i]-s[i-1]<=1

例题

模版题

https://www.luogu.com.cn/problem/P5960

思路

直接敲SPFA
注意：
（1）节点0和各边都要连一个边权为0的边，且起点从0开始
（2）SPFA判出负环(cnt[t]>n)就说明无解

代码

const int N=5e3+10;
int n,m;
vector<PII> g[N];
int dist[N],cnt[N];//cnt判负环
bool st[N];
bool SPFA(int s,int n){
	memset(dist,0x3f,sizeof dist);
	dist[s]=0;
	queue<int> q;
	q.push(s);
	while(q.size()){
		int t=q.front();
		if(cnt[t]>n) return false;//判负环
		q.pop();
		st[t]=0;
		for(auto son:g[t]){
			int pos=son.fi;
			int val=son.sc;
			if(val+dist[t]<dist[pos]){
				dist[pos]=val+dist[t];
				if(!st[pos]){
					q.push(pos);
					st[pos]=1;
					cnt[pos]++;
				}
			}
		}
	}
	return true;
}
void solve(){
    cin>>n>>m;
	for(int i=1;i<=m;i++){
		int u,v,w;
		cin>>u>>v>>w;
		g[v].push_back({u,w});
	}
	for(int i=1;i<=n;i++){
		g[0].push_back({i,0});
	}
    if(SPFA(0,n)){
		for(int i=1;i<=n;i++) cout<<dist[i]<<" ";
	}
	else cout<<"NO"<<endl;
}

种树

利用数列建图
https://www.luogu.com.cn/problem/P1250

思路

注意本题正解是贪心

两个约束条件：
(1)从区域b到e至少要包含t棵树：
前缀和s[e]-s[b-1]>=t
->无法转化，所以本题求的是*最长路*
(2)※最容易漏
每个位置只能种1棵树
0<=s[i]-s[i-1]<=1
->
s[i]-s[i-1]>=0
s[i-1]-s[i]>=-1

代码

const int N=3e4+10;
int n,h;
vector<PII> g[N];
int dist[N];
bool st[N];
void SPFA(int s,int n){
	for(int i=1;i<=n;i++) dist[i]=-inf_int;
	dist[s]=0;
	queue<int> q;
	q.push(s);
	while(q.size()){
		auto t=q.front();
		st[t]=0;
		q.pop();
		for(auto son:g[t]){
			int pos=son.fi;
			int val=son.sc;
			if(dist[pos]<dist[t]+val){
				dist[pos]=dist[t]+val;
				if(!st[pos]){
					q.push(pos);
					st[pos]=1;
				}
			}
		}
	}
}
void solve(){
    cin>>n>>h;
	for(int i=1;i<=h;i++){
		int b,e,t;
		cin>>b>>e>>t;
		//s[e]-s[b-1]>=t ->求最长路
		g[b-1].push_back({e,t});
	}
	//第二个约束条件：每一个地块只能种一棵树 
	//0<=s[i]-s[i-1]<=1
	//-> s[i]-s[i-1]>=0
	//   s[i-1]-s[i]>=-1
	for(int i=1;i<=n;i++){
		g[i-1].push_back({i,0});
		g[i].push_back({i-1,-1});
	}
	
    for(int i=1;i<=n;i++){
		g[0].push_back({i,0});
	}
	
	SPFA(0,n);
	int ans=dist[n];
	cout<<ans<<endl;
}

参考：
https://zhuanlan.zhihu.com/p/104764488
https://www.zybuluo.com/DATASOURCE/note/164437
https://www.cnblogs.com/jffifa/archive/2012/05/12/2497072.html