【全排列】

【全排列】

性质

若干个不同的数 可以组成多少个不同的序列

全排列个数：\(n!\)
求解全排列：dfs+回溯

题目整理

小红与好数组

https://ac.nowcoder.com/acm/contest/112320/D
求和的全排列+附加条件
按字典序从小到大输出->每次dfs都从1开始for

代码

const int N=22;
int n;
int ans[N];
void dfs(int sum,int u){//一个是和，一个是层数
    if(sum<0) return;
    if(sum==0){
        for(int i=0;i<u;i++){
            cout<<ans[i]<<" ";
        }
        cout<<endl;
    }
    for(int i=1;i<=n;i++){
        if((!u) || (u && ans[u-1]!=i)){//注意相邻的不能相等
            ans[u]=i;
            dfs(sum-i,u+1);
            ans[u]=0;
        }
    }
}
void solve(){
    cin>>n;
    dfs(n,0);
}

[2024CCPC Online]军训II

https://codeforces.com/gym/105336

题目大意

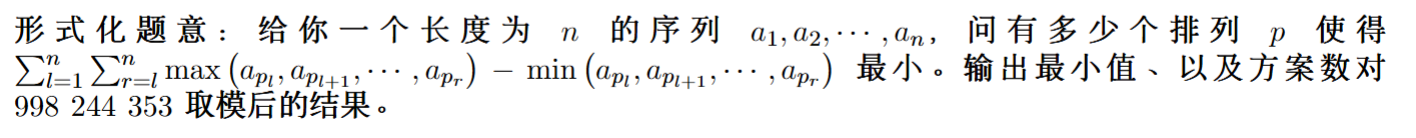
思路

结论：整齐度最小的序列是排过序的序列->正排反排均可->答案$ \times 2$

相同数之间可以任意排：对答案贡献是全排列个数
注意所有数都相同->正反排没区别->不用$ \times 2$

代码

int n;
i64 frac(int x){
    i64 res=1;
    for(int i=1;i<=x;i++){
        res=(i64)i*res%mod;
    }
    res%=mod;
    return res;
}
void solve(){
    cin>>n;
    vector<int> a(n+1,0);
    map<int,int> mp;
    for(int i=1;i<=n;i++){
        cin>>a[i];
        mp[a[i]]++;
    }
    sort(a.begin()+1,a.end(),cmp);
    i64 ans=0,res=1;
    for(auto [key,val]:mp){
        res=frac(val)*res%mod;
    }
    if(mp.size()>1) res=res*2LL%mod;
    for(int i=1;i<=n;i++){
        for(int j=i+1;j<=n;j++){
            ans+=(i64)(a[j]-a[i]);
        }
    }
    cout<<ans<<" "<<res<<endl;
}

[2025ICPC Online II]Tree Shuffling

【容斥+LCA计数】
https://codeforces.com/gym/106072/problem/H

题目大意

把这个描述进行转化

一棵树，点权位\(a_i=i\)，选一条路径，可以随机打乱其中的点。问能得到多少个不同的树，两棵树在一个点的点权不同即视为不同。

思路

区分两条路径的方式：端点是不变的

n为1e3->考虑钦定两个端点暴力->计算每条链的全排列
※注意：如果端点不变换那么会算重->端点一定需要变换
->考虑容斥：去掉头尾端点不变换的个数，加上中间变换的个数

代码

int n;
i64 ans=0;
i64 frac[N];
//提前打阶乘表
void calf(){
    frac[1]=1LL;
    for(int i=2;i<=3000;i++){
        frac[i]=frac[i-1]*(i64)i%mod;
    }
}
void solve(){
    cin>>n;
    //init
    ans=0;
    tree.init(n);
    for(int i=1;i<n;i++){
        int u,v;
        cin>>u>>v;
        tree.add(u,v);
    }
    tree.work();
	//直接暴力枚举两点即可
    for(int i=1;i<=n;i++){
        for(int j=i+1;j<=n;j++){
            i64 cnt=tree.clac(i,j)+1;
            i64 res1=frac[cnt];
            i64 res2=frac[cnt-1]*2LL%mod;
            i64 res3=frac[cnt-2];
            i64 res=((res1+mod-res2)%mod+res3)%mod;
            ans=(ans+res)%mod;
        }
    }
    ans=(ans+n)%mod;//注意最后要加n
    cout<<ans<<endl;
    tree.clear();
}