【博弈论】理论基础

【博弈论】理论基础

概念

初始状态很重要！一般都是针对初始状态进行讨论
必胜态
必败态

巴什博弈(Bash Game)

就是取石子

模型

结论

若n%(m+1)!=0 先手赢
若n%(m+1)==0 后手赢

分析

（1）若n%(m+1)!=0
先手可以拿到剩下(m+1)整数倍的石子留给后手
后手无论如何没办法拿完（只能拿1-m个）
->留给后手永远没办法拿完->后手必败态->先手必胜态
（2）若n%(m+1)==0
先手无论如何拿不完->先手必败态

例题

质数次方版取石子

https://www.luogu.com.cn/problem/P4018

结论

若n%6!=0 先手赢
若n%6==0 后手赢

分析

打表可以取的石子
1 可以
2 可以
3 可以
4 可以
5 可以
6=2*3 题目只能构造1个质数作为因数->不行
->既然6不能被取 那么如果想赢 最后留给对面的一定要是6的倍数->这样对面无论如何也取不完->我就可以取完
->若n%6!=0 先手可以给后手构造出n%6==0
->若n%6==0 先手最后都会面对 因为后手也知道要给先手构造n%6==0

Nim博弈

模型

https://www.luogu.com.cn/problem/P2197

结论

必胜态：所有数字异或起来不为0
必败态：所有数字异或起来为0

分析

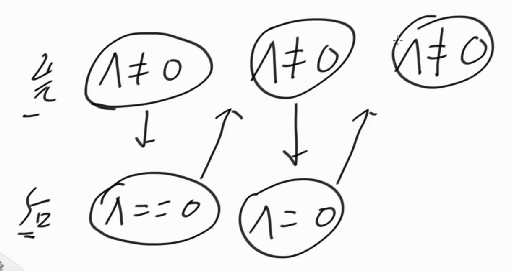
（1）在拿到所有数字异或完为0时，无论取几个，都无法改变异或完不为0的状态

只要取小，就一定会改变一个数每个位上0和1的状态->奇偶一定会变->异或结果一定会变

（2）在拿到所有数字异或完不为0时，都一定可以通过拿取，变为异或完为0的状态

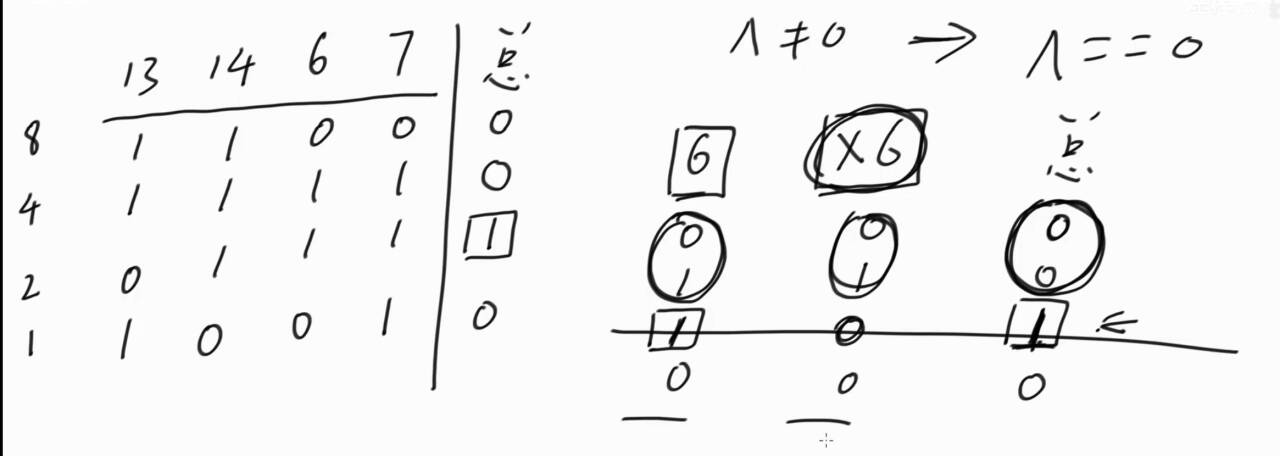
所有数异或完的结果 最高位的1对应过去 哪一个数字的该位上是1 拿这一堆就可以 一定可以通过变小达成结果

例题

反Nim博弈（反常游戏）

https://www.luogu.com.cn/problem/P4279

结论

(1)若初始即为1 1 1 1 1 ...型：按奇偶
 若n%2==0 先手赢
 若n%2!=0 后手赢
(2)若初始为随机：可构造为x>1 1 1 1 1 ...的形式进行操纵->此时为必胜态
->看谁能拿到x>1 1 1 1 1 ...
->观察到x>1 1 1 1 1 ...异或结果一定!=0
->若异或结果不为0 先手赢
  若异或结果为0   后手赢
※※看谁先拿到必胜态

代码

int n;
void solve(){
    cin>>n;
    vector<int> a(n+1,0);
    for(int i=1;i<=n;i++) cin>>a[i];
    int cnt=0;
    int huo=a[1];
    if(a[1]==1) cnt++;
    for(int i=2;i<=n;i++){
        if(a[i]==1) cnt++;
        huo=huo^a[i];
    }
    if(cnt==n){
        if(n%2){
            cout<<"Brother"<<endl;
        }
        else{
            cout<<"John"<<endl;
        }
    }
    else{
        if(huo==0){
            cout<<"Brother"<<endl;
        }
        else{
            cout<<"John"<<endl;
        }
    }
}