【区间/线段问题】
(贪心)【区间/线段问题】
模型整理
题目整理
注意不要推一些看上去简单又对的结论
数据范围小优先想想暴力+贪心
中场撸猫
https://ac.nowcoder.com/acm/contest/101921/D
正确结论
麻将塔的第一次层选择第一行最小的数字
之后每一层 除了最后一个 都选择这一层中不小于这一个点的右父亲的那个数字
(要遍历一遍上层数组->相当于暴力)
最后一个选择不小于左父亲的即可
->记得特判!
错误结论
下一行二分查找大于等于上一行左端点的数即可
hack数据:
1 100 101 102
2 3 101 102
4 5 6 101
5 5 5 5
代码
#include<bits/stdc++.h>
using namespace std;
#define endl '\n'
typedef pair<int,int> PII;
typedef long long ll;
ll abss(ll a){return a>0?a:-a;}
ll max_(ll a,ll b){return a>b?a:b;}
ll min_(ll a,ll b){return a<b?a:b;}
bool cmpll(ll a,ll b){return a>b;}
const int N=1e3+10;
int t;
int n;
int b[N][N];
void solve(){
cin>>n;
for(int i=1;i<=n;i++) for(int j=1;j<=n;j++) cin>>b[i][j];
for(int i=1;i<=n;i++) sort(b[i]+1,b[i]+1+n);
//倾向于选小数
int ans=1;
vector<int> up;
up.push_back(b[1][1]);
bool is_ok=true;
for(int i=2;i<=n;i++){
vector<int> tmp;
int l=1,r=n+1;
for(auto a : up){
//二分查找
r=n+1;
while(l<r){
int mid=(l+r)>>1;
if(b[i][mid]>=a) r=mid;
else l=mid+1;
}
if(l==n+1){
is_ok=false;
break;
}
else{
tmp.push_back(b[i][l]);
l++;
}
}
//处理最后一个数
r=n+1;
while(l<r){
int mid=(l+r)>>1;
if(b[i][mid]>=up[up.size()-1]) r=mid;
else l=mid+1;
}
if(l==n+1){
break;
}
else{
tmp.push_back(b[i][l]);
}
if(!is_ok) break;
up=tmp;
ans++;
}
cout<<ans<<endl;
}
signed main(){
ios::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
cin>>t;
while(t--) solve();
return 0;
}
小紫的线段染色
https://ac.nowcoder.com/acm/contest/103948/E
思路
先考虑无解的情况:当一个点有三条及以上线段叠在一起时->差分求解
->※此时一定有解
按区间左端点排序 对重合进行反色处理->^操作
※※※注意存线段id->排序后会乱序 不能直接输出i !!!
代码
#include<bits/stdc++.h>
using namespace std;
#define endl '\n'
typedef pair<int,int> PII;
typedef long long ll;
ll abss(ll a){return a>0?a:-a;}
ll max_(ll a,ll b){return a>b?a:b;}
ll min_(ll a,ll b){return a<b?a:b;}
bool cmpll(ll a,ll b){return a>b;}
const int N=1e5+10;
int t=1;
int n;
struct node{
int l,r,id;//记录id是为了记录第几条线段:注意线段不一定是有序的!
};
bool cmp(node x,node y){
if(x.l!=y.l) return x.l<y.l;
return x.r<y.r;
}
void solve(){
cin>>n;
vector<node> q(n+1);
vector<PII> d;//1e9:离散化差分:直接推+排序
for(int i=1;i<=n;i++){
int l,r;
cin>>l>>r;
q[i].l=l;q[i].r=r;q[i].id=i;
d.push_back({l,1});
d.push_back({r+1,-1});
}
sort(d.begin(),d.end());
int sum=0;
bool is_ok=true;
for(auto &[x,y]:d){
sum+=y;
if(sum>2){
is_ok=false;
break;
}
}
if(!is_ok) cout<<"-1";
else{
sort(q.begin()+1,q.end(),cmp);
vector<int> ans(n+1,0);
int k=0;
int r=-1,id=0;
for(int i=1;i<=n;i++){
if(q[i].l>r){
r=q[i].r;
id=q[i].id;
}
else if(q[i].l<=r){
ans[q[i].id]=ans[id]^1;
k++;
}
}
if(k==0){//注意特判不需要染色的情况:至少染一个
cout<<1<<endl;
cout<<1;
}
else{
cout<<k<<endl;
for(int i=1;i<=n;i++){
if(ans[i]) cout<<i<<" ";
}
}
}
}
signed main(){
ios::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
//cin>>t;
while(t--) solve();
return 0;
}
Manhattan Pairs
https://codeforces.com/contest/2122/problem/C
题目大意
二维坐标系
n个点两两配对,求曼哈顿距离总和最大
思路
1|2
-----
3|4
如果把坐标分成4个象限:2和3配对 1和4配对是最优的
->以一个轴分两半,块内交叉即可
代码
const int N=3e5+10;
int n;
void solve(){
cin>>n;
vector<array<i64,3>> q(n+1);
for(int i=1;i<=n;i++){
int a,b;
cin>>a>>b;
q[i]={a,b,i};
}
sort(q.begin()+1,q.end(),[&](array<i64,3> x,array<i64,3> y)->bool{
return x[0]<y[0];
});
vector<array<i64,3>> q1,q2;
for(int i=1;i<=n/2;i++){
q1.push_back(q[i]);
q2.push_back(q[n-i+1]);
}
sort(q1.begin(),q1.end(),[&](array<i64,3> x,array<i64,3> y)->bool{
return x[1]<y[1];
});
sort(q2.begin(),q2.end(),[&](array<i64,3> x,array<i64,3> y)->bool{
return x[1]>y[1];
});
for(int i=0;i<n/2;i++){
cout<<q1[i][2]<<" "<<q2[i][2]<<endl;
}
}
【区间和点匹配】Canvas Painting
https://qoj.ac/contest/2513/problem/14303
题目大意

思路
(1)连边肯定在相邻两点之间最优
->把连边当成位置,有\(n-1\)个连边,把区间右端点-1
->转化为区间和点匹配的问题
(2)从点的角度考虑:从左到右考虑每个点
选择所有覆盖它的区间中右端点最小的进行匹配一定最优
(3)从区间的角度考虑:把所有区间按照右端点排序再依次考虑每个区间,每次选择该区间内部最靠左且没匹配的点即可
代码
int n,m;
void solve(){
cin>>m>>n;
vector<PII> a(m+1);
for(int i=1;i<=m;i++){
cin>>a[i].fi>>a[i].sc;
}
sort(a.begin()+1,a.end(),[&](PII x,PII y)->bool{
if(x.sc!=y.sc) return x.sc<y.sc;
return x.fi<y.fi;
});
//记得特判1!
if(n==1){
cout<<1<<endl;
return;
}
set<PII> pos;pos.insert({1,n-1}); //当前尚未被打通的 “连续连接点区间”
int ans=n;
//优先打通最靠左的点
for(int i=1;i<=m;i++){
auto [l,r]=a[i];
r--;
if(l>r) continue;
auto it=pos.upper_bound({l,n});
//优先找<=l的最大
bool st=0;
if(it!=pos.begin()){
//若 tmp 包含 l,说明 l 是当前魔法区间 [l, r] 内最靠左的可用连接点
auto tmp=it;tmp--;
if(tmp->fi<=l && l<=tmp->sc){
ans--;
st=1;
int L=tmp->fi,R=tmp->sc;
pos.erase(tmp); //l点被覆盖了,拆成两个区间
//注意判断区间有效!因为有r-1
if(L<=l-1) pos.insert({L,l-1});
if(l+1<=R) pos.insert({l+1,R});
}
}
if(st) continue;
//然后考虑>l的交集
if(it!=pos.end()){ //能找到且为交集
int L=it->fi,R=it->sc;
if(L>r) continue;
//打通当前区间最靠左的连接点L
pos.erase(it);
ans--;
if(L+1<=R) pos.insert({L+1,R});
}
}
cout<<ans<<endl;
}
小红出千
【双指针处理区间映射问题】
https://ac.nowcoder.com/acm/contest/125954/G
题目大意

思路
错误贪心思路:b[i]=a[i]-a[1]-i;后找众数
hack数据:
8
5 5 6 7 6 10 11 12
正确思路:区间肯定为\([L,L+n-1]\)
将数组排序去重映射到数轴上,
后采用双指针(快慢指针) 对应区间
找包含在区间内的种类数num,答案为n-num
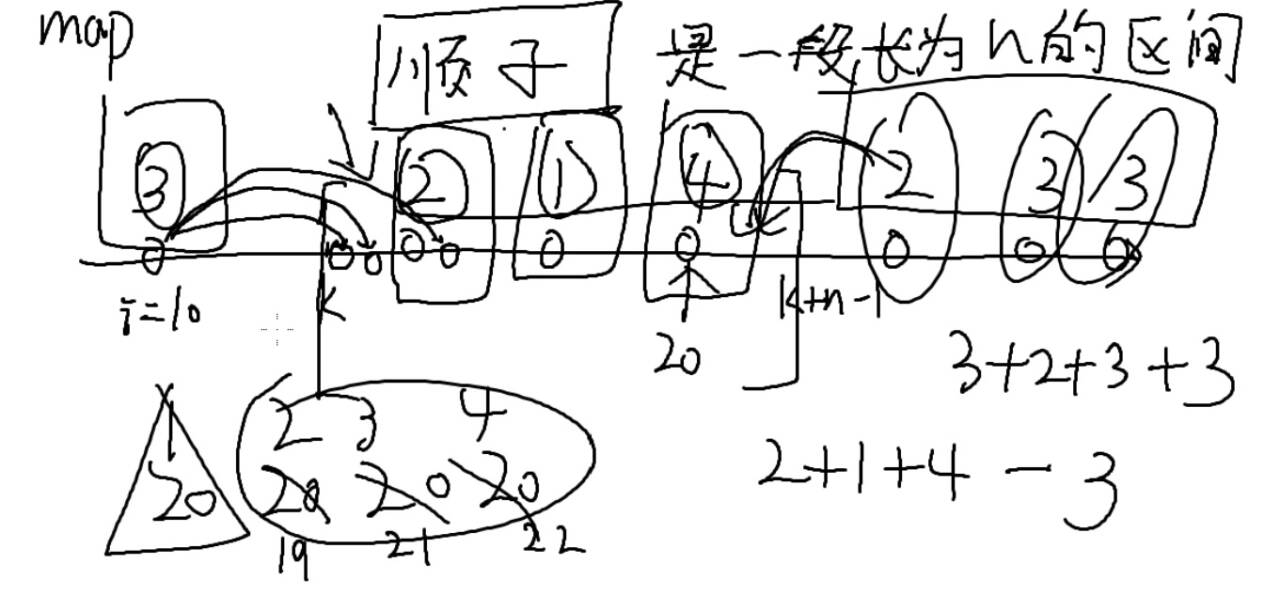
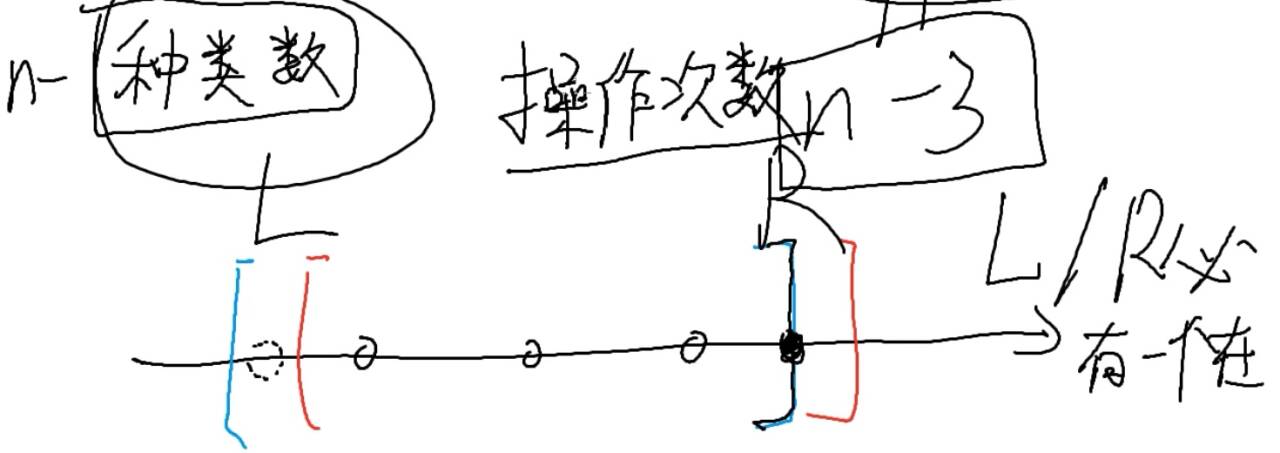
代码
int n;
void solve(){
cin>>n;
vector<int> a(n+1,0);
for(int i=1;i<=n;i++) cin>>a[i];
if(n==1){
cout<<0<<endl;
return;
}
map<int,int> pos;
for(int i=1;i<=n;i++) pos[a[i]]++;
vector<int> st;
for(auto [key,val]:pos){
st.push_back(key);
}
int lst=st.size();
/*
cout<<lst<<endl;
for(auto son:st) cout<<son<<" ";
cout<<endl;
*/
int l=0,r=0;
int num=-1,po=0;
for(r=0;r<lst;r++){
while(st[r]>(st[l]+n-1)){
l++;
}
int len=r-l+1;
if(len>num){
num=len;
po=l;
}
//cout<<l<<' '<<r<<endl;
}
//cout<<num<<' '<<po<<endl;
if(num==-1){
cout<<0<<endl;
return;
}
int ans=n-num;
cout<<ans<<endl;
map<int,int> st3;
vector<int> st2(n+1,0);
int idx=st[po];
int L=st[po],R=st[po]+n-1;
for(int i=1;i<=n;i++){
if(!st3[a[i]] && a[i]>=L && a[i]<=R){
st3[a[i]]=i;
st2[i]=1;
}
}
for(int i=1;i<=n;i++){
if(st2[i]) continue;
while(st3[idx]) idx++;
cout<<i<<" "<<idx<<endl;
st3[idx]=1;
st2[i]=1;
}
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号