【分块】
【分块】
依照某种规律把一组数分成块 块内具有相同性质->可方便计算
设阈值分治->一部分分块 一部分单独算
【整除分块】
O(sqrt(n)) 支持n<=1e12

核心思想
打表可得:

可发现:

时间复杂度分析

做法

【模版代码】
注意取模操作!
i64 division_block(i64 n){
i64 res=0;
for(i64 l=1LL,r;l<=n;l=r+1LL){
r=n/(n/l);
i64 cnt=(r-l+1)%mod;
i64 val=(n/l)%mod;
res=(res+(cnt*val)%mod)%mod;
}
return res;
}
题目整理
【二分+分块】智乃与模数
https://ac.nowcoder.com/acm/contest/95335/G
思路
代码
注意运用了很多等差数列的结论与变形计算
#include<bits/stdc++.h>
using namespace std;
#define endl '\n'
typedef pair<int,int> PII;
typedef long long ll;
ll abss(ll a){return a>0?a:-a;}
ll max_(ll a,ll b){return a>b?a:b;}
ll min_(ll a,ll b){return a<b?a:b;}
bool cmpll(ll a,ll b){return a>b;}
/*
【思路】
打表->发现每个商相同的可以分为一组->余数为等差数列->公差为商
找前k个数:排完序后有单调性->二分第k个数的数值x(大于等于x的数至少有k个) 去check里验证并求和
【余数的表示方式】
a/b=x......t
->余数 t=a-向下取整(a/b)*b
*/
ll n,k;
ll vtot=0,val=0;
ll check(ll x){
ll tot=0;//计算余数>=x的情况下有多少个
for(ll l=1,r;l<=n;l=r+1){
r=n/(n/l);//右区间
ll a=n-(n/l)*l; //余数->首项(最大的那个)
ll b=n/l; //商->公差
if(a<x) continue;
/*计算个数:末项a-b*(len-1)>=x -> len<=(a-x)/b+1*/
tot+=min_((a-x)/b+1,r-l+1);//(a-x)/b+1:区间内余数>=k的个数
}
return tot;
}
signed main(){
ios::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
cin>>n>>k;
ll L=1,R=n+1;
while(L<R){
ll mid=(L+R)/2;
//找小于第k个的第一个
ll tot_=check(mid);
if(tot_>=k){// 数量大于等于k 左端点右移 ※值变大 范围变小
L=mid+1;
}
else{
R=mid;
val=mid;
vtot=tot_;
}
}
ll ans=(k-vtot)*(val-1);
for(ll l=1,r;l<=n;l=r+1){
r=n/(n/l);//右区间
ll a=n-(n/l)*l; //余数->首项(最大的那个)
ll b=n/l; //商->公差
if(a<val) continue;
ll len=min_((a-val)/b+1,r-l+1);
ans+=(a+a-b*(len-1))*len/2;
}
cout<<ans;
return 0;
}
https://ac.nowcoder.com/acm/problem/17450
Count A%B=C
https://atcoder.jp/contests/abc414/tasks/abc414_e
题目大意
在1~n中找数互不相等的三元组(a,b,c),使得a%b=c,求三元组个数(取模)
n<=1e12
思路
※注意n~b中b的倍数个数:[n/b]向下取整

代码
注意取模要预处理
//整除分块 : 求1~n中 n/i 的总和
i64 division_block(i64 n){
i64 res=0;
for(i64 l=1LL,r;l<=n;l=r+1LL){
r=n/(n/l);
i64 cnt=(r-l+1)%mod;
i64 val=(n/l)%mod;
res=(res+(cnt*val)%mod)%mod;
}
return res;
}
const int N=3e5+10;
i64 n;
void solve(){
cin>>n;
i64 n_mod=n%mod;
i64 n1_mod=(n-1LL)%mod;
i64 ans=(n_mod*n_mod)%mod;
i64 res1=(n1_mod*n_mod)%mod*qmi(2LL,mod-2LL,mod)%mod;
ans=(ans+mod-res1)%mod;
i64 res2=division_block(n);
ans=(ans+mod-res2)%mod;
cout<<ans<<endl;
}
【倍数/因数分块】
越小的数倍数越多->需要一起算
【模版代码】预处理因数/倍数/GCD/LCM
//因数
int cnt[N];
vector<int> g[N];
//倍数
int G[B+6][B+6];
i64 lcm(i64 x,i64 y){
if(x==0 || y==0) return (x+y);
return x/G[x][y%x]*y;
}
void init(){
//预处理因数
for(int i=1;i<=n;i++){
for(int j=1;j<=n/i;j++){
g[i*j].push_back(i);
}
}
for(int i=1;i<=n;i++) cnt[i]=g[i].size();
for(int i=1;i<=B;i++){
for(int j=1;j<=n/i;j++){
//枚举倍数
}
}
//GCD表
for(int i=0;i<=B;i++){
for(int j=0;j<=B;j++){
if(i==0 || j==0){
G[i][j]=i+j;
}
else if(i<j){
G[i][j]=G[j%i][j];
}
else{
G[i][j]=G[i%j][j];
}
}
}
}
题目整理
Multiple and Factor
https://acm.hdu.edu.cn/contest/problem?cid=1181&pid=1002
题目大意

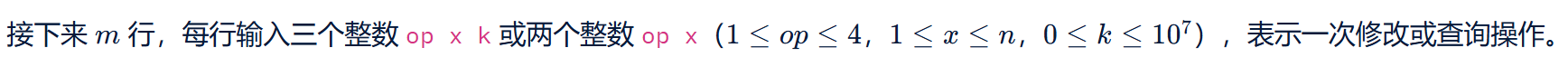
思路
越小的数倍数越多->分块加
因数没多少个->直接暴力加即可
注意本题gcd和lcm计算要处理成O(1)->提前打GCD表
代码
const int N=5e5+10;
const int B=300;//分块阈值
int n,m;
i64 a[N];
//因数
int cnt[N];
vector<int> g[N];
//倍数
int G[B+6][B+6];
i64 c[N];//小值修改记录
i64 sum[N];//i的倍数和
i64 lcm(i64 x,i64 y){
if(x==0 || y==0) return (x+y);
return x/G[x][y%x]*y;
}
void init(){
//预处理因数
for(int i=1;i<=n;i++){
for(int j=1;j<=n/i;j++){
g[i*j].push_back(i);
}
}
//因数个数
for(int i=1;i<=n;i++) cnt[i]=g[i].size();
//预处理倍数和
for(int i=1;i<=B;i++){
for(int j=1;j<=n/i;j++){
sum[i]+=a[i*j];
}
}
//预处理gcd表:注意这里复杂度是O(1)的 打表不用单算
for(int i=0;i<=B;i++){
for(int j=0;j<=B;j++){
if(i==0 || j==0){
G[i][j]=i+j;
}
else if(i<j){
G[i][j]=G[j%i][j];
}
else{
G[i][j]=G[i%j][j];
}
}
}
}
void solve(){
cin>>n>>m;
for(int i=1;i<=n;i++) cin>>a[i];
init();
while(m--){
int op,x;
cin>>op>>x;
if(op==1){
i64 k;
cin>>k;
if(x<=B){
c[x]+=k;
}
else{
for(int i=x;i<=n;i+=x){
a[i]+=k;
}
}
//更新sum
for(int i=1;i<=B;i++){
sum[i]+=1LL*k*(n/lcm(i,x));//lcm(i,x)既是i倍数又是x倍数
}
}
else if(op==2){
i64 k;
cin>>k;
for(auto son:g[x]){
a[son]+=k;
}
for(int i=1;i<=B;i++){
if(x%i==0){
sum[i]+=1LL*k*cnt[x/i];
}
}
}
else if(op==3){
if(x<=B){
cout<<sum[x]<<endl;
}
else{
//a中大数直接算和
i64 ans=0;
for(int i=x;i<=n;i+=x){
ans+=a[i];
}
//需要加上小数c加倍数的贡献
for(int i=1;i<=B;i++){
ans+=c[i]*(n/lcm(i,x));//小数同样能是大数的倍数
}
cout<<ans<<endl;
}
}
else if(op==4){
i64 ans=0;
for(auto son:g[x]){
ans+=a[son];
if(son<=B){//还需要加上小数c加倍数的贡献
ans+=c[son]*cnt[x/son];// *cnt[x/son]:son倍数中同时也是x因数的部分
}
}
cout<<ans<<endl;
}
}
}
杂题整理
最努力的活着
https://acm.hdu.edu.cn/contest/problem?cid=1179&pid=1009
题目大意

思路
放置是上帝视角:从低到高保留即可
有暴力代码
i128 n,w;
void solve(){
read(n);read(w);
i128 nn=n;
i128 ans=0;
while(n>=w){
ans+=nn*n-n*(n-1)/2;
n-=n/w;
}
ans+=nn*n-n*(n-1)/2;
write(ans);
putchar('\n');
}
考虑分块优化

代码
i128 n,w;
const i128 K=100;
void solve(){
read(n);read(w);
i128 N=n,ans=0;
while(n>=w){
i128 q=n/w;
if(q==0)break;
i128 mn=q*w;//当前n中有多少个w
i128 s_q=(n-mn)/q+1; //分值为q的块大小
s_q=max128(s_q,1);
//同时n不能小于w
i128 s_w=(n-w)/q+1;
i128 s=min128(s_q,s_w);
s=min128(s,(i128)100000);
//算贡献:块递减大小为q 有s个块
if(s>K){
i128 a=n;
i128 last=a-(s-1)*q;//算第s步的n值:注意剪前(s-1)步
i128 b=a-s*q;//下一轮迭代的n值
i128 sx=s*(a+last)/2;
i128 sx2=a*a*s-a*q*s*(s-1)+q*q*(s-1)*s*(2*s-1)/6;
ans+=((2*N+1)*sx-sx2)/2;
n=b;
}
else{
for(i128 i=0;i<s&&n>=w;i++){
ans+=n*(2*N-n+1)/2;
n-=q;
}
}
}
//注意最后<w的块也需要加
ans+=n*(2*N-n+1)/2;
write(ans);
putchar('\n');
}
Symmetry Intervals 2
https://ac.nowcoder.com/acm/contest/108298/H
16进制分块
struct FenwickTree {
vector<int> tree;
int size;
FenwickTree(int n){
size=n;
tree.resize(n+1,0);
}
void update(int pos, int delta){
for(;pos<=size;pos+=pos&-pos)
tree[pos]^=delta;
}
int query(int pos){
int res=0;
for(;pos>0;pos-=pos&-pos)
res^=tree[pos];
return res;
}
};
const int N=1e6+10;
const int M=1<<16;
int n,q;
string str=" ";
int s[N];
us mask[N];
int pre[M],suf[M],in[M];
/*
【翻转操作】
树状数组:处理块的翻转
tag_d:*暴力*处理边界的翻转
*/
int tag_d[N];
void solve(){
read(n);
read(q);
FenwickTree ft(n);
for(int i=1;i<=n;i++){
char c=nc();
if(c=='0' || c=='1') str+=c;
}
for(int i=1;i<=n;i++){
s[i]=str[i]&1;
}
for(int i=1;i<=n;i++){
for(int j=0;(i+j)<=n&&j<16;j++){
if(s[i+j]) mask[i]|=(1<<j);
//mask:以每个点为起始点,往下数16个
}
}
//init:算1<<16种块,每一种块的前缀后缀和中间的*连续1子串*产生的贡献
for(int i=0;i<M;i++){
int cnt=0;
bool fl=true;
for(int j=0;j<16;j++){
if((i>>j)&1){
cnt++;
}
else{
if(fl){//前缀
pre[i]=cnt;
fl=false;
}
else{
in[i]+=((cnt+1)*cnt)>>1;
}
cnt=0;
}
}
if(fl){//全1
pre[i]=suf[i]=16;
}
else{
suf[i]=cnt;
}
}
while(q--){
int op;
read(op);
if(op==1){
int l,r;
read(l);read(r);
if((r-l)<15){//块内翻转:对于包含了l到r的所有块,都需要暴力标记一下"要翻转"
for(int i=max(1,l-15);i<=r;i++){
int u=max(0,l-i);
int v=min(15,r-i);
us flip=((1<<(v-u+1))-1)<<u;
mask[i]^=flip;
}
}
else{
//左边界
for(int i=max(1,l-15);i<l;i++){
int u=max(0,l-i);
int v=min(15,r-i);
us flip=((1<<(v-u+1))-1)<<u;
mask[i]^=flip;
tag_d[i]^=1;
}
//右边界
for(int i=max(1,r-14);i<=r;i++){
int u=max(0,l-i);
int v=min(15,r-i);
us flip=((1<<(v-u+1))-1)<<u;
mask[i]^=flip;
}
//中间
ft.update(l,1);
ft.update(r-14,1);
tag_d[l]^=1;
//中间块边界
for(int i=max(1,r-29);i<=r-14;i++){
tag_d[i]^=1;
}
}
}
else if(op==2){
int l,a,b;
read(l);read(a);read(b);
int tag=ft.query(a)^ft.query(b);
i64 ans=0;
int cnt=0;
for(int i=0;i<l;i+=16){
us cur=mask[i+a]^mask[i+b];
if(!tag) cur=~cur;
if(i+15>=l) cur&=(1<<(l-i))-1;
//全1
if(pre[cur]==16){
cnt+=16;
}
else{
cnt+=pre[cur];
ans+=(((i64)cnt+1LL)*(i64)cnt)>>1LL;
ans+=in[cur];
cnt=suf[cur];
}
tag^=tag_d[i+a+1]^tag_d[i+b+1];
}
ans+=(((i64)cnt+1LL)*(i64)cnt)>>1LL;
write(ans);
putchar('\n');
}
}
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号