【欧拉函数】

【欧拉函数】

运用

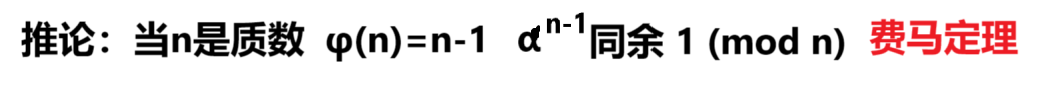
公式求欧拉函数

时间复杂度 O(sqrt(n))

//公式法求欧拉函数 
#include<bits/stdc++.h>
using namespace std;
#define endl '\n'
typedef long long ll;
int n;
ll a;
signed main(){
      ios::sync_with_stdio(0);
      cin.tie(0);
      cout.tie(0);
      cin>>n;
      while(n--){
      	cin>>a;
      	ll res=a;
      	//分解质因数 
      	for(int i=2;i<=a/i;i++) {
      		if(a%i==0){
      			res=res/i*(i-1);//都是整数 所以不要写分数形式 
      			while(a%i==0) a/=i;
			}
		}
		if(a>1) res=res/a*(a-1);
		cout<<res<<endl;
	}
      return 0;
}

筛法求欧拉函数

求1~n中每一个数的欧拉函数
时间复杂度 O(n)

#include<bits/stdc++.h>
using namespace std;
#define endl '\n'
typedef long long ll;
const int N=1000010;
int t;
int primes[N],cnt;
bool st[N];
int phi[N];
ll get_eulers(int n){
	//线性筛质数打底 
	phi[1]=1;//特别定义 
	for(int i=2;i<=n;i++){
		if(!st[i]){
			primes[cnt++]=i;
			phi[i]=i-1;//i是质数的情况下，其他所有比他小的数都能和他互质 
		}
		for(int j=0;primes[j]<=n/i;j++){
			st[primes[j]*i]=true;
			if(i%primes[j]==0){
				//pj是质数->没法被分解 
				//当i%pj==0时->φ(pj*i) =pj * φ(i) 
				phi[primes[j]*i]=primes[j]*phi[i];
				break;
			}
			//多了一个质因子->多乘一个(1-1/pj) 
			//i%pj!=0时-> φ(pj*i) =(pj-1) * φ(i)  
			phi[primes[j]*i]=(primes[j]-1)*phi[i];
		}
	}
	ll res=0;
	for(int i=1;i<=n;i++) res+=phi[i];
	return res;
}
signed main(){
      ios::sync_with_stdio(0);
      cin.tie(0);
      cout.tie(0);
      cin>>t;
      ll ans=get_eulers(t);
      cout<<ans; 
      return 0;
}