【质数】

【质数】

判定质数：试除法

时间复杂度 O(sqrt(n))

思路

代码

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
int t,a;
bool is_prime(int n){
	if(n<2) return false;
	//注意这里细节：尽量不要写成i<=sqrt(n) 或者 i*i<=n 
	for(int i=2;i<=n/i;i++){
		if(n%i==0) return false;
	}
	return true;
}
signed main(){
      ios::sync_with_stdio(0);
      cin.tie(0);
      cout.tie(0);
      cin>>t;
      while(t--){
      	cin>>a;
      	if(is_prime(a)) cout<<"Yes"<<"\n";
      	else cout<<"No"<<"\n";
	}
      return 0;
}

分解质因数：试除法

时间复杂度 最好O(logn) 最坏O(sqrt(n))

思路

（1）从小到大枚举所有数
（2）n中最多只包含一个大于sqrt(n)的质因子
->先枚举小于sqrt(n)的 再单独输出一次

代码

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
int t,a;
void divide(int n){
	for(int i=2;i<=n/i;i++){
		//细节：这里不需要特别去判质数
		/*
		先除的2 那么就把2的倍数全部除掉了
		先除的3 那么就把3的倍数全部除掉了
		以此类推 
		*/ 
		if(n%i==0){
			//判次数
			int s=0;
			while(n%i==0){
				n/=i;//直接更新n 
				s++;
			}
			cout<<i<<" "<<s<<"\n";
		}
	}
	//单独输出一次大于sqrt(n)的质数（注意特判n>1防止n被除完而输出1） 
	if(n>1) cout<<n<<" 1"<<"\n";
	cout<<"\n";
}
signed main(){
      ios::sync_with_stdio(0);
      cin.tie(0);
      cout.tie(0);
      cin>>t;
      while(t--){
      	cin>>a;
      	divide(a);
	}
      return 0;
}

筛质数：埃式筛法（埃筛）

思路

（1）朴素算法：从小到大把该数的倍数删掉 O(nlogn)
（2）优化：只需要删质数的倍数 O(nloglogn)->O(n)

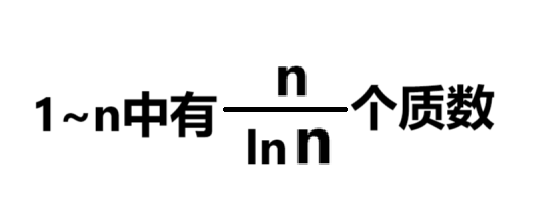
质数定理

代码

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N=1000010;
int t; 
int primes[N],cnt;
bool st[N];
void get_primes(int n){
	for(int i=2;i<=n;i++){
		if(st[i]) continue;//只需要筛质数 
		primes[cnt++]=i;//记录质数 
		for(int j=i+i;j<=n;j+=i){//把倍数全部删掉 
			st[j]=true;
		}
	}
}
signed main(){
      ios::sync_with_stdio(0);
      cin.tie(0);
      cout.tie(0);
      cin>>t;
      get_primes(t);
      cout<<cnt;
      return 0;
}

筛质数：线性筛法（欧拉筛）

更快

思路

O(n)
1.对于每个数n，只会被它的最小质因子筛掉
分类讨论：
（1）i%primes[j]==0
     primes[j]一定是i的最小质因子
     primes[j]一定是primes[j]*i的最小质因子
（2）i%primes[j]!=0
     primes[j]一定小于i的所有质因子（要继续找更大的质因子）
     primes[j]也一定是primes[j]*i的最小质因子
->不管什么情况 primes[j]一定是primes[j]*i的最小质因子->primes[j]*i被筛掉
2.对于一个合数x，一定有一个最小质因子
  当i枚举到i/primes[j]时 x就会被筛掉

代码

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N=1000010;
int t; 
int primes[N],cnt;
bool st[N];
void get_primes(int n){
	for(int i=2;i<=n;i++){
		if(!st[i]) primes[cnt++]=i;//是质数 
		//小细节：不用写j<=cnt -> 一定会在小于cnt时停下 
		//primes[j]<=n/i -> 把大于n的合数筛去没意义 
		for(int j=0;primes[j]<=n/i;j++){//找每一个质因子 
			st[primes[j]*i]=true;//最小质因子的倍数都是合数->筛去 
			if(i%primes[j]==0) break;//primes[j]一定小于i的所有质因子（要继续找更大的质因子）
		}
	}
}
signed main(){
      ios::sync_with_stdio(0);
      cin.tie(0);
      cout.tie(0);
      cin>>t;
      get_primes(t);
      cout<<cnt;
      return 0;
}

题目积累

质数筛法

LCM Sequence（区间筛素数）

用埃筛写

https://atcoder.jp/contests/abc412/tasks/abc412_e

区间筛素数做法

设区间为L，R
（1）如果一个数x不是质数：至少在sqrt(x)范围内有1个因子
->先把sqrt(R)内的所有质数筛出（线性筛法即可）
（2）遍历质数表：对于一个质数pr
找(L+pr-1)/pr*pr到R/pr*pr的所有pr倍数 并筛去
（3）没被筛到的数就是质数

题目大意

思路

【思路】能让lcm变化仅有两种方式：
（1）该数为质数
->素数筛的区间筛法：
判断1e14内的一个数不是质数：一定有一个sqrt(1e14)=1e7内的因数
->把1e7内的质数全部筛去->用埃筛的方式筛去所有合数

（2）质数的幂次：质因子只有1个
->想到2^64也才循环64次->暴力求解即可

代码

const int N=1e7+10;
i64 l,r;
bool vis[N];
void solve(){
    cin>>l>>r;
	if(l==r){
		cout<<1<<endl;
		return;
	}
	get_primes(N);
    for(int i=0;i<primes_cnt;i++){
		if(primes[i]>r) break;
		//（1）
		i64 x=(l+primes[i]-1LL)/primes[i]*primes[i];
		i64 y=r/primes[i]*primes[i];
		for(i64 k=x;k<=y;k+=primes[i]){
			vis[k-l]=1;
		}
	}
	for(int i=0;i<primes_cnt;i++){
		if(primes[i]>r) break;
		//（2）
		i64 pr=primes[i];
		while(pr<=r){
			if(pr>l) vis[pr-l]=0;//注意这里不是>=l：第一个数不用累计
			pr*=primes[i];
		}
	}
	int sz=r-l+1;
	int ans=1;
	for(int i=1;i<sz;i++) if(!vis[i]) ans++;//注意第一个数不累计->从l+1开始
	cout<<ans<<endl;
}