python数据挖掘初体验——COVID19数据可视化分析挖掘

数据说明：

来源： https://www.kesci.com/mw/project/5e68db4acdf64e002c97b413/dataset

（ncov）

• 日期：从2020年1月21日开始

• 累计确诊：当日累计确诊

• 全国新增确诊：全国当日新增确诊

• 湖北新增确诊：湖北省当日新增确诊

• 累计疑似：实为当日全国现有疑似

• 新增疑似：当日新增疑似

• 现有重症：当日现有重症

• 新增重症：当日新增重症，若减少统计为0

• 累计死亡：当日累计死亡

• 全国新增死亡：当日全国新增死亡

• 湖北新增死亡：当日湖北省新增死亡

• 累计治愈：当日全国累计治愈

• 全国新增治愈：当日全国新增治愈

• 湖北新增治愈：当日湖北省新增治愈

• 当日密切接触：当日全国新增密切接触，为当日累计密接减去截止前一天累计密接人数

• 当日解除观察：当日全国解除观察

• 累计继续观察：截至当日剩余继续观察

• 累计入境：截至当日累计确诊入境人员，从3月1日开始统计（3月1、2、3日国家卫健委未通报入境确诊情况，数据来自其他地方，可能不准确）

• 新增入境：当日入境人员新增确诊，从3月1日开始统计（3月1、2、3日国家卫健委未通报入境确诊情况，数据来自其他地方，可能不准确）

（beijing_local）

数据仅包含从6月11日开始北京本地患者变化情况，不包含境外患者。

• 日期：从2020年6月11日至2020年7月31日

• 累计确诊：当日累计确诊

• 累计治愈：当日累计治愈

• 累计死亡：当日累计死亡

• 现有无症状：截至当日现有无症状感染者

• 新增确诊：当日新增确诊

• 新增治愈：当日新增治愈

• 新增死亡：当日新增死亡

• 新增疑似：截至当日新增疑似

• 新增无症状：截至当日新增无症状感染者

思路分析：

我把重心放在数据挖掘上，所以没有自己爬数据，所以使用的数据是已有的清洗过的干净的数据。数据来源于

首先是从磁盘中读取文件：，采用with open打开文件，然后使用read_csv 读取文件

代码如下：

with open('E:/DM/data/ncov.csv')as f:

data = pd.read_csv(f)

date_list = list(data['日期'])

confirm_list = list(data['累计确诊'])

suspect_list = list(data['累计疑似'])

dead_list = list(data['累计死亡'])

heal_list = list(data['累计治愈'])

1. 数据测试：

   f =open('E://DM/data/ncov.csv')

   df1 = pd.read_csv(f)

测试数据是否正确可读，结果如图：

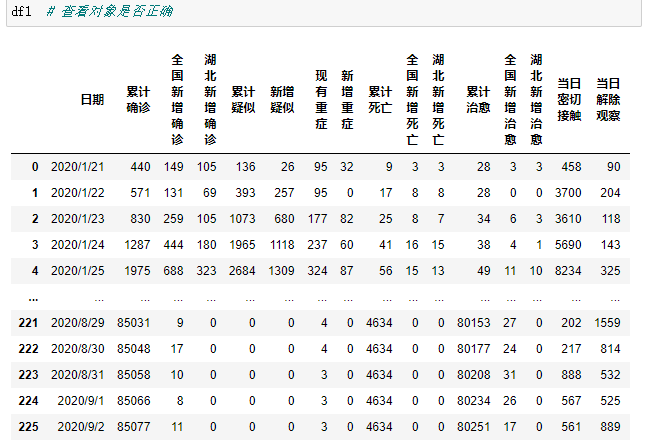
然后通过pyecharts
模块绘制折线图，绘制累计确诊、累计疑似等数据的曲线图，输出到output目录下：

结果如下：

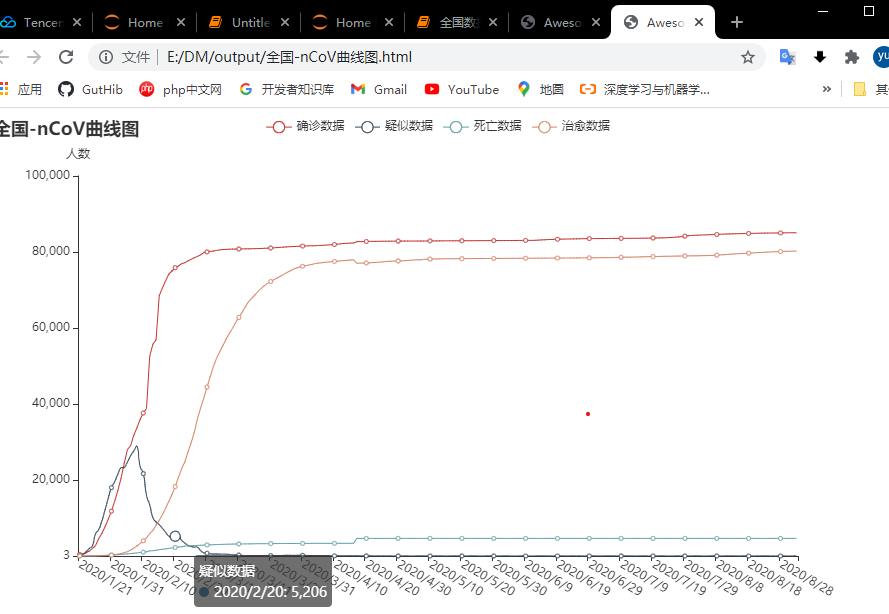
同理，读取北京地区的数据，通过.add_xaxis 方法将北京的数据中时间加入pyecharts
的对象中，作为横坐标，然后把其他数据加入横坐标中，绘制图像后保存到bei_jing的HTML中，如下图：

然后是绘制全国数据的折线面积图：核心代码如下：

line = (

Line()

.add_xaxis(date_list)

.add_yaxis('确诊数据', confirm_list, is_smooth=True,

markline_opts=opts.MarkLineOpts(data=[opts.MarkLineItem(type_="average")]))

.add_yaxis('疑似数据', suspect_list, is_smooth=True,

markline_opts=opts.MarkLineOpts(data=[opts.MarkLineItem(type_="average")]),)

.add_yaxis('死亡数据', dead_list, is_smooth=True,

markline_opts=opts.MarkLineOpts(data=[opts.MarkLineItem(type_="average")]),)

.add_yaxis('治愈数据', heal_list, is_smooth=True,

markline_opts=opts.MarkLineOpts(data=[opts.MarkLineItem(type_="average")]),)

# 隐藏数字 设置面积

.set_series_opts(

areastyle_opts=opts.AreaStyleOpts(opacity=0.5),

label_opts=opts.LabelOpts(is_show=False))

# 设置x轴标签旋转角度

.set_global_opts(xaxis_opts=opts.AxisOpts(axislabel_opts=opts.LabelOpts(rotate=-30)),

yaxis_opts=opts.AxisOpts(name='人数', min_=3),

title_opts=opts.TitleOpts(title='2019-nCoV曲线图'))

)

line.render('E:/DM/output/全国-nCoV曲线面积图2.html')

结果如图：

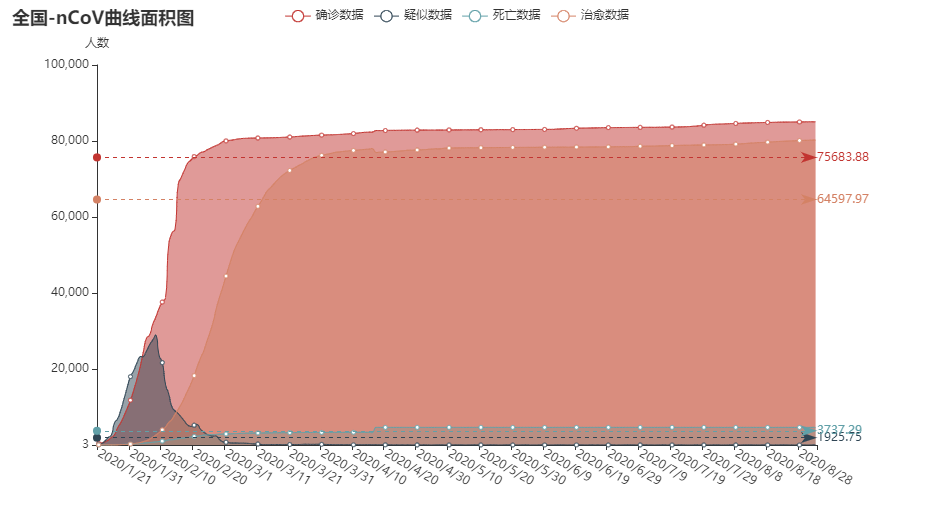
最后是在第二个分析的基础上，加上最大值和最小值

更改代码：

opts.MarkPointOpts(data=[opts.MarkPointItem(type_="max"),

opts.MarkPointItem(type_="min")]))

运行结果如下：

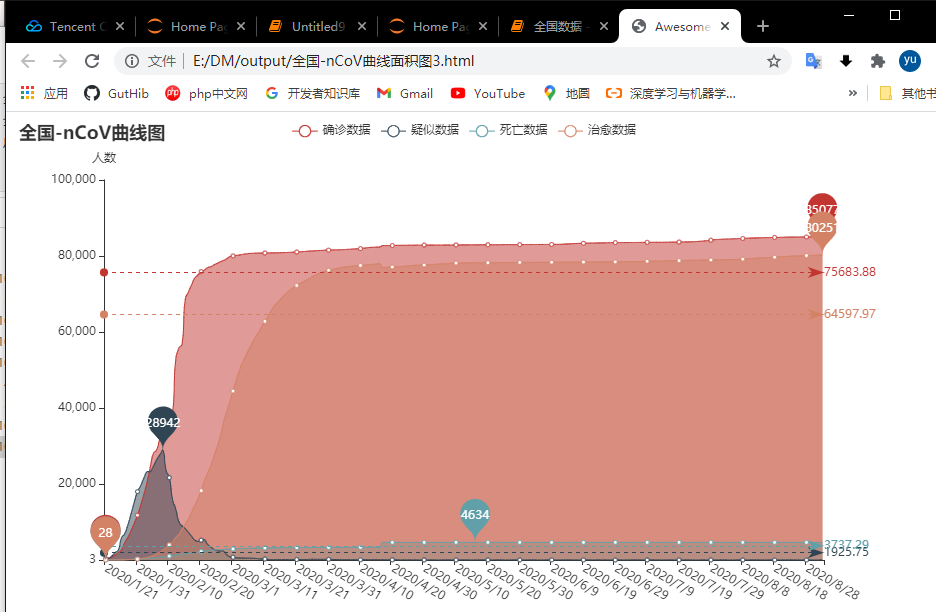
第二部分是基于确诊人数的预测分析。

1、首先是通过数据建立函数模型，通过 matlab的扩展绘制出来。

核心代码如下：

t = range(len(confirm)) # 构建作图的横坐标

fig = plt.figure(figsize=(10,4))

ax = fig.add_subplot(1,1,1)

ax.scatter(t,confirm,color="k",label="确诊人数") #真实数据散点图

#ax.set_xlabel("天数") #横坐标

ax.set_ylabel("确诊人数") #纵坐标

ax.set_title("确诊人数变化") #标题

ax.set_xticklabels(['', '2020/1/21', '2020/2/21', '2020/3/21',
'2020/4/21','2020/5/21','2020/6/21'], rotation=30, fontsize=10)
#自定义横坐标标签

得出的拟合函数如图所示：

1. 拟合

   查阅资料知道对于人数增长的模型，一般logistic模型进行拟合用

   需要先定义出函数表达式，这里采用logistic函数，因为从散点图可以看到这些散点大致分布在“S”形曲线的前半部分上，logistic函数表达式如下

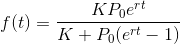
查阅资料得知：

K为环境容量，即增长到最后，f(t)能达到的极限
P0为初始容量，就是t=0时刻的数量。
r为增长速率，r越大则增长越快，越快逼近K值，r越小增长越慢，越慢逼近K值。
首先定义出logistic函数，其中K,P0,r是待求的参数，然后调用from
scipy.optimize里面的curve_fit函数进行拟合，会得到拟合参数，接着把拟合曲线也绘制出来

核心代码如下：

def logistic(t,K,P0,r): #定义logistic函数

exp_value=np.exp(r*(t))

return (K*exp_value*41)/(K+(exp_value-1)*41)

coef, pcov = curve_fit(logistic, t, confirm) #拟合

print(coef) #logistic函数参数

y_values = logistic(t,coef[0],coef[1],coef[2]) #拟合y值

plt.plot(t,y_values,color="blue",label="拟合曲线") #画出拟合曲线

绘制得到如图所示的曲线：

最后一部分 是通过获得的拟合曲线，预测结果

代码如下：

x=np.linspace(23,46,24) #构造期货日期

y_predict=logistic(x,coef[0], coef[1], coef[2]) #未来预测值

ax.scatter(x,y_predict, color="green",label="未来预测") #未来预测散点

ax.legend() #加标签

ax.plot(x,y_predict,color="blue", label="预测曲线")

得出的结果如下：

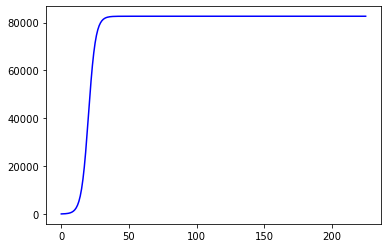
可以看到最终的结果是跟预测分析的结果几乎一模一样

我认为这时因为数据集很大，包括了从1月21日开始一直到9月21日的全部数据，所以拟合度很高，几乎一模一样，但也说明了拟合的正确性

遇到的问题：

1）、当我尝试输入日期和确诊人数的绘图时，notebook报错

Image size of 4490273x485 pixels is too large. It must be less than 2^16 in
each direction

图片像素过大，无法输出。

最终选择导出为html文件，因为html文件的兼容性，很好的解决这个问题。

实验总结：

这次实验所有的实验过程都是基于jupyter
notebook，也是一次全新的尝试，发现notebook在做分析时效率很明显，不用去配置环境变量，基于anaconda的环境使得使用起来很方便。

实验过程中查阅的大量的资料，也是第一次真正的接触数据挖掘，作业开始之前请教一位这方面的师兄，有没有比较速成的数据挖掘入门的教程，得到这样一句话：

确实是这样。

实验中深刻的认识到，数学和计算机科学本来就是同一门学科，就想起一大佬的一句话：

“统计学做不到的人工智能也做不到“。

还要继续加油，要学的东西还有好多。