KNN算法
1、KNN算法基本介绍
KNN（K-Nearest Neighbors，K - 近邻）是一种简单、直观、无参数的惰性学习算法，核心思想是认为 “物以类聚、人以群分”，通过待预测样本与训练集中 “最近邻” 样本的相似度，推断其类别（分类任务）或数值（回归任务）。它无需训练模型参数，仅在预测时计算距离，广泛应用于分类、回归、推荐系统等场景。
1.1、核心原理（3 步理解）
KNN 通过距离度量判断样本间的 “远近”（相似度），距离越近，相似度越高。
常用距离公式有
- 欧氏距离（最常用），计算公式为对应维度差值平方和，开平方根
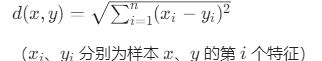
- 曼哈顿距离（城市街区距离），计算公式为对应维度差值的绝对值之和。如[1,2]、[3,5]，值则为5
- 切比雪夫距离，计算公式为对应维度差值的绝对值中的最大值。如[1,2]、[3,5]，值则为3
- 闵可夫斯基距离（闵氏距离），这并不是一种距离度量方式，只是对多种距离度量公式的概括性的表达
K 的大小直接影响模型拟合效果：
- K 过小（如 K=1）：过度依赖单个样本，易受噪声 / 异常值影响，导致过拟合；
- K 过大（如 K≈训练集样本数）：过度平滑，忽略局部特征，导致欠拟合；
- 最优 K：通过交叉验证（如 5 折交叉验证）+ 网格搜索（测试 K=3、5、7...31）选择。
- 分类任务：对 K 个最近邻样本的类别进行 “多数投票”，得票最多的类别作为预测结果。例：K=5 时，最近邻样本类别为 [猫、猫、狗、猫、兔]，预测结果为 “猫”（3 票胜出）。
- 回归任务：对 K 个最近邻样本的数值取 “平均值”（或加权平均值），作为预测结果。例：K=3 时，最近邻样本房价为 [100 万、120 万、110 万]，预测房价 =（100+120+110）/3=110 万。
1.2、KNN 的核心特性（优缺点）
1.3、适用场景与不适用场景
2、KNN算法API（scikit-learn）
scikit-learn（简称 sklearn）是 Python 生态中最成熟、最流行的开源机器学习库，基于 numpy（数值计算）和 scipy（科学计算）构建，专注于传统机器学习算法的工程化实现，提供了从数据预处理到模型部署的全流程工具链，是入门机器学习、快速验证算法思路、甚至工业级应用的首选工具。scikit-learn 是开源免费的，基于 BSD 许可证，可商业使用。
scikit-learn 的安装参考：https://www.cnblogs.com/wenxuehai/p/18542054#_label2_0
2.1、分类API
KNN 分类 API如下，可参考官网api：https://scikit-learn.org/stable/modules/generated/sklearn.neighbors.KNeighborsClassifier.html
class sklearn.neighbors.KNeighborsClassifier(n_neighbors=5, *, weights='uniform', algorithm='auto', leaf_size=30, p=2, metric='minkowski', metric_params=None, n_jobs=None)
示例代码如下：
""" KNN算法介绍(K Nearest Neighbors), K近邻算法 原理: 基于 欧式距离(或者其它距离计算方式)计算 测试集 和 每个训练集之间的距离, 然后根据距离升序排列, 找到最近的K个样本. 基于K个样本投票, 票数多的就作为最终预测结果 -> 分类问题. 基于K个样本计算平均值, 作为最终预测结果 -> 回归问题. 实现思路: 1. 分类问题 适用于: 有特征, 有标签, 且标签是不连续的(离散的) 2. 回归问题. 适用于: 有特征, 有标签, 且标签是连续的. KNN算法, 分类问题思路如下: 1. 计算测试集和每个训练的样本之间的 距离. 2. 基于距离进行升序排列. 3. 找到最近的K个样本. 4. K个样本进行投票. 5. 票数多的结果, 作为最终的预测结果. 代码实现思路: 1. 导包. 2. 准备数据集(测试集 和 训练集) 3. 创建(KNN 分类模型)模型对象. 4. 模型训练. 5. 模型预测. """ # 1. 导包. from sklearn.neighbors import KNeighborsClassifier # 分类 # 2. 准备数据集(测试集 和 训练集) x_train = [[0], [1], [2], [3]] # 训练集的特征数据, 因为特征可以有多个特征, 所以是一个二维数组，如[[1,1], [1,4], [2,1], [3,9]] y_train = [0, 0, 1, 1] # 训练集的标签数据, 因为标签是离散的, 所以是一个一维数组 x_test = [[5]] # 测试集的特征数据 # 3. 创建(KNN 分类模型)模型对象. # estimator: 估计器, 模型对象, 也可以用变量名 model做接收. estimator = KNeighborsClassifier(n_neighbors=3) # 4. 模型训练 # 传入: 训练集的特征数据, 训练集的标签数据 estimator.fit(x_train, y_train) # 5. 模型预测. # 传入: 测试集的特征数据, 获取到: 预测结果(测试集的标签, y_test) y_pre = estimator.predict(x_test) # 6. 打印预测结果. print(f'预测值为: {y_pre}')
上面执行结果如下：
2.2、回归API
KNN 回归 API如下，可参考官网api：https://scikit-learn.org/stable/modules/generated/sklearn.neighbors.KNeighborsRegressor.html
class sklearn.neighbors.KNeighborsRegressor(n_neighbors=5, *, weights='uniform', algorithm='auto', leaf_size=30, p=2, metric='minkowski', metric_params=None, n_jobs=None)
示例代码如下：
""" KNN算法介绍(K Nearest Neighbors), K近邻算法 原理: 基于 欧式距离(或者其它距离计算方式)计算 测试集 和 每个训练集之间的距离, 然后根据距离升序排列, 找到最近的K个样本. 基于K个样本投票, 票数多的就作为最终预测结果 -> 分类问题. 基于K个样本计算平均值, 作为最终预测结果 -> 回归问题. 实现思路: 1. 分类问题 适用于: 有特征, 有标签, 且标签是不连续的(离散的) 2. 回归问题. 适用于: 有特征, 有标签, 且标签是连续的. KNN算法, 回归问题思路如下: 1. 计算测试集和每个训练的样本之间的 距离. 2. 基于距离进行升序排列. 3. 找到最近的K个样本. 4. 基于K个样本的标签值, 计算平均值. 5. 将上述计算出来的平均值, 作为最终的预测结果. 代码实现思路: 1. 导包. 2. 准备数据集(测试集 和 训练集) 3. 创建(KNN 回归模型)模型对象. 4. 模型训练. 5. 模型预测. 总结: K值过小, 容易受到异常值的影响, 且会导致模型学到大量的"脏的特征", 导致出现: 过拟合. K值过大, 模型会变得简单, 容易发生: 欠拟合. """ # 1. 导包. from sklearn.neighbors import KNeighborsRegressor # KNN算法的 回归模型 # 2. 准备数据集(测试集 和 训练集) x_train = [[0, 0, 1], [1, 1, 0], [3, 10, 10], [4, 11, 12]] # 训练集的特征数据, 因为特征可以有多个特征, 所以是一个二维数组 y_train = [0.1, 0.2, 0.3, 0.4] # 训练集的标签数据, 因为标签是连续的, 所以是一个一维数组 x_test = [[3, 11, 10]] # 测试集的特征数据 # 3. 创建(KNN 回归模型)模型对象. estimator = KNeighborsRegressor(n_neighbors=2) # 4. 模型训练. estimator.fit(x_train, y_train) # 5. 模型预测. y_pre = estimator.predict(x_test) # 6. 打印预测结果. print(f'预测值为: {y_pre}')
上面执行结果如下：
3、常见距离计算方法
KNN（K - 近邻）算法的核心是通过距离度量衡量样本间的相似度（距离越近，相似度越高），不同距离计算方法适用于不同数据类型（连续型、高维、稀疏数据等）。
3.1、欧式距离（Euclidean Distance）
欧式距离是最经典的距离度量，可以理解为两个点在空间中的距离。
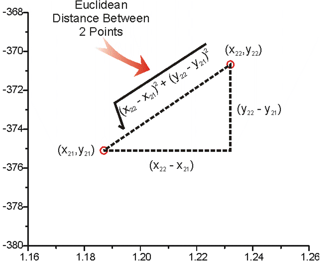
计算公式为：
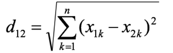（即对应维度差值平方和，然后开平方根）
举个例子：AB 两点为 [[1,1],[2,2]] ，计算 AB 距离，经计算得: AB = √(2−1)^2 +(2−1)^2 = √ 2 = 1.414
典型案例：
3.2、曼哈顿距离（Manhattan Distance）
也称为城市街区距离。
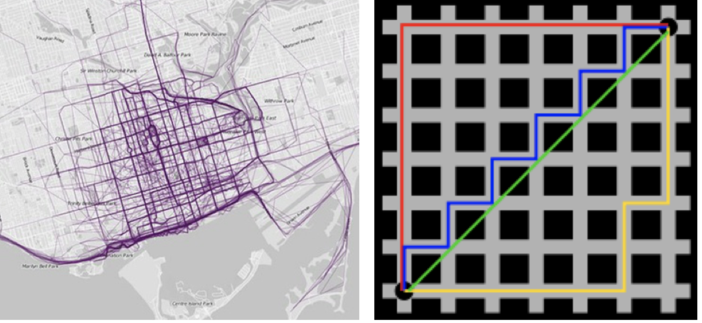
计算公式为：
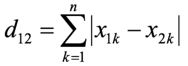（对应维度差值的绝对值之和）
举个例子： AB 点为[ [1,1], [2,2]] ， 计算AB 曼哈顿距离 经计算得: AB =|2−1|+ ⌈2−1⌉= 2
典型案例：
3.3、切比雪夫距离（Chebyshev Distance）
在国际象棋中，国王可以直行、横行、斜行，所以国王走一步可以移动到相邻8个方格中的任意一个。 国王从格子(x1,y1)走到格子(x2,y2)最少需要多少步？这个距离就叫切比雪夫距离。
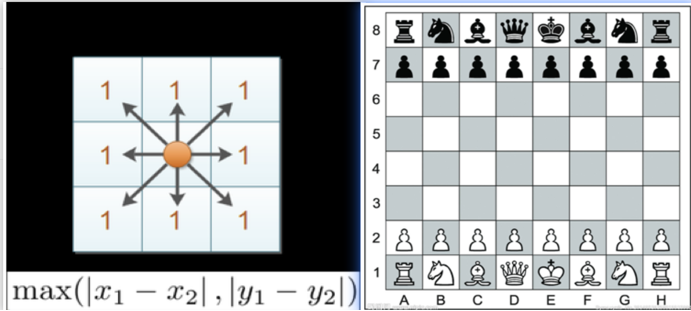
计算公式为：
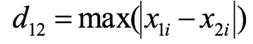（即对应维度差值的绝对值中的最大值）
举个例子： AB 点为 [ [1,1], [2,3] ] ， 计算AB曼哈顿距离，经计算得: AB =max(|2−1|, ⌈3−1⌉) = 2
3.4、闵可夫斯基距离（Minkowski Distance）
也称为闵氏距离，闵氏距离不是一种新的距离的度量方式，而是欧氏距离、曼哈顿距离、切比雪夫距离的统一泛化表达，通过参数 p 控制距离类型。
定义为：
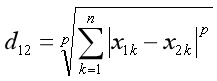
其中p是一个变参数，根据 p 的不同，闵氏距离可表示某一类种的距离：
- 当 p=1 时，就是曼哈顿距离；
- 当 p=2 时，就是欧氏距离；
- 当 p→∞ 时，就是切比雪夫距离
4、特征预处理
特征预处理是特征工程的一部分，特征预处理的两种核心方法 —— 归一化（Min-Max Scaling）和标准化（Standard Scaling），它们的核心目的都是消除特征的量级差异、统一数据尺度，避免因特征范围不一致导致模型误判或性能下降。
比如，假设有两个特征：「身高（m）」范围 [1.5, 2.0]，「体重（kg）」范围 [40, 100]。在 KNN 的欧氏距离计算中，经平方值放大后，身高的差异（如 0.5m）权重远小于体重的差异（如 60kg），导致模型过度关注 “体重” 而忽略 “身高”—— 这就是特征量级不一致的危害。归一化 / 标准化的作用就是将所有特征映射到同一尺度，让每个特征对模型的影响更均衡。
4.1、归一化（Min-Max Scaling，缩放到固定区间）
归一化就是通过对原始数据进行变换把数据映射到某个数值区间（如 [mi, mx]），默认为 [0,1] 。由于归一化方法非常容易受异常点影响，所以一般比较少用。
转换到 [0, 1] 区间的公式为：
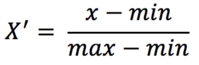
如果转换区间不是 [0, 1] 而是其他值，如 [mi, mx]，在上面公式基础上继续以下计算：
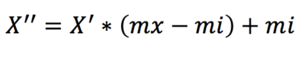
示例：假设特征「体重（kg）」的原始数据为 [40, 60, 80, 100]： min(x)=40 ， max(x)=100 ； 对 60kg 归一化： (60−40)/(100−40)=20/60≈0.333 ； 对 100kg 归一化： (100−40)/(100−40)=1 ； 以此类推计算出结果：[0, 0.333, 0.667, 1]。
4.1.1、归一化API
API 如下，可参考官网：https://scikit-learn.org/stable/modules/generated/sklearn.preprocessing.MinMaxScaler.html
class sklearn.preprocessing.MinMaxScaler(feature_range=(0, 1), *, copy=True, clip=False) # feature_range 缩放区间
示例代码：
# 导包 from sklearn.preprocessing import MinMaxScaler # 归一化对象 # 1. 准备数据集(归一化之前的原数据). x_train = [[90, 2, 10, 40], [60, 4, 15, 45], [75, 3, 13, 46]] # 2. 创建归一化对象. # 参数feature_range 表示生成范围, 默认为: 0, 1 如果就是这个区间, 则参数可以省略不写. transfer = MinMaxScaler() # transfer = MinMaxScaler(feature_range=(3, 5)) # 可以指定区间 # 3. 对原数据集进行归一化操作. x_train_new = transfer.fit_transform(x_train) # 4. 打印处理后的数据. print('归一化后的数据集为: \n') print(x_train_new)
执行后输出结果如下：
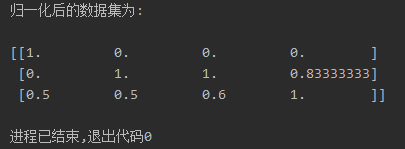
4.2、标准化（Standard Scaling/Z-Score 标准化，缩放到正态分布）
标准化是将特征值映射到均值为 0、标准差为 1 的正态分布（也叫 Z-Score 转换）。该方法对异常值不敏感，比较常用。
公式：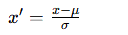
- x ：原始特征值
- x ′ ：标准化后的特征值
- μ （mu）：该特征的均值
- σ （sigma）：该特征的标准差，公式为
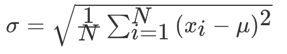
示例，特征「体重（kg）」数据 [40, 60, 80, 100]： 均值 μ=(40+60+80+100)/4=70 ； 标准差 σ≈22.36； 对 60kg 标准化： (60−70)/22.36≈−0.447 ； 对 100kg 标准化： (100−70)/25.82≈1.341； 结果：[[-1.34164079], [-0.4472136 ], [ 0.4472136 ], [ 1.34164079]]（均值≈0，标准差≈1）。
核心特点：
- 优点：对异常值稳健（异常值的影响被标准差稀释，不会过度压缩正常数据）
- 缺点：结果范围不固定（通常在 [-3, 3] 之间，因正态分布 99.7% 数据在 ±3σ 内）；
- 适用场景：数据近似正态分布、存在异常值、模型对数据分布有要求的场景（如 KNN、SVM、线性回归、逻辑回归等大多数机器学习模型）。
4.2.1、标准化API
API 如下，可参考官网：https://scikit-learn.org/stable/modules/generated/sklearn.preprocessing.StandardScaler.html#
class sklearn.preprocessing.StandardScaler(*, copy=True, with_mean=True, with_std=True)[source]#
使用代码示例：
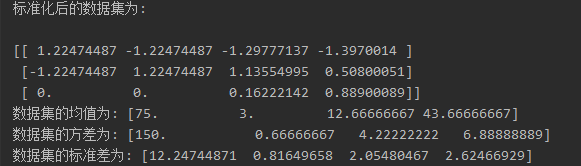
# 导包 from sklearn.preprocessing import StandardScaler # 标准化对象 # 1. 准备数据集(标准化之前的原数据). x_train = [[90, 2, 10, 40], [60, 4, 15, 45], [75, 3, 13, 46]] # 2. 创建标准化对象. transfer = StandardScaler() # 3. 对原数据集进行标准化操作. x_train_new = transfer.fit_transform(x_train) # 4. 打印处理后的数据. print('标准化后的数据集为: \n') print(x_train_new) # 5. 打印数据集的均值和方差. print(f'数据集的均值为: {transfer.mean_}') print(f'数据集的方差为: {transfer.var_}') print(f'数据集的标准差为: {transfer.scale_}')
执行后输出结果如下：
浙公网安备 33010602011771号