452. Minimum Number of Arrows to Burst Balloons

There are a number of spherical balloons spread in two-dimensional space. For each balloon, provided input is the start and end coordinates of the horizontal diameter. Since it's horizontal, y-coordinates don't matter and hence the x-coordinates of start and end of the diameter suffice. Start is always smaller than end. There will be at most 104 balloons.

An arrow can be shot up exactly vertically from different points along the x-axis. A balloon with xstart and xend bursts by an arrow shot at x if xstart ≤ x ≤ xend. There is no limit to the number of arrows that can be shot. An arrow once shot keeps travelling up infinitely. The problem is to find the minimum number of arrows that must be shot to burst all balloons.

Example:

Input:
[[10,16], [2,8], [1,6], [7,12]]

Output:
2

Explanation:
One way is to shoot one arrow for example at x = 6 (bursting the balloons [2,8] and [1,6]) and another arrow at x = 11 (bursting the other two balloons).

class Solution {
    public int findMinArrowShots(int[][] points) {
            if (points.length == 0) {
                return 0;
            }
            Arrays.sort(points, (a, b) -> a[1] - b[1]);// Arrays.sort(points, (a, b) -> Integer.compare(a[1], b[1]));
            int arrowPos = points[0][1];
            int arrowCnt = 1;
            for (int i = 1; i < points.length; i++) {
                if (arrowPos >= points[i][0]) {
                    continue;
                }
                arrowCnt++;
                arrowPos = points[i][1];
            }
            return arrowCnt;
        }
}

 

 56 Merge Intervals <- very similar😈
435 Non-overlapping Intervals <- very similar😈
252 Meeting Rooms
253 Meeting Rooms II

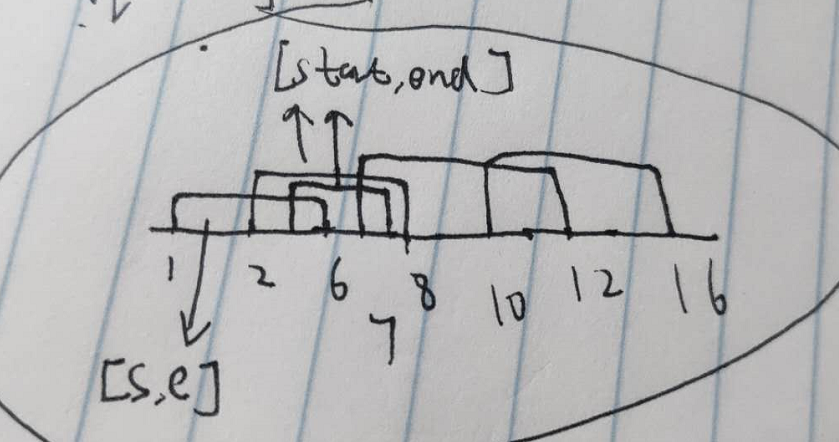
说为啥像merge interval？

仔细一看，就像是merge inteval里面的merge情况，e ≥ start就可以合并，这里我们合并就是可以用一个arrow射爆，那么第一个【s，e】可以合并三个，然后更新【s，e】继续往下

 有个问题啊，就是Integer的界限问题在用Arrays.sort(points, (a, b) -> a[1] - b[1])体现，因为a[1] - b[1]会越界，所以以后都要用 Arrays.sort(points, (a, b) -> Integer.compare(a[1], b[1]));来写