518. Coin Change 2
You are given coins of different denominations and a total amount of money. Write a function to compute the number of combinations that make up that amount. You may assume that you have infinite number of each kind of coin.
Example 1:
Input: amount = 5, coins = [1, 2, 5] Output: 4 Explanation: there are four ways to make up the amount: 5=5 5=2+2+1 5=2+1+1+1 5=1+1+1+1+1
Example 2:
Input: amount = 3, coins = [2] Output: 0 Explanation: the amount of 3 cannot be made up just with coins of 2.
Example 3:
Input: amount = 10, coins = [10] Output: 1
Note:
You can assume that
- 0 <= amount <= 5000
- 1 <= coin <= 5000
- the number of coins is less than 500
- the answer is guaranteed to fit into signed 32-bit integer
class Solution { public int change(int amount, int[] coins) { int[] dp = new int[amount + 1]; dp[0] = 1; for (int j = 0; j < coins.length; j++) { for (int i = 1; i <= amount; i++) { if (i - coins[j] >= 0) { dp[i] += dp[i - coins[j]]; } } } return dp[amount]; } }

dp[i] = dp[i - coins[0]] + dp[i - coins[1]] + ... + dp[i - coins[coins.length - 1]] if i - coins[0] >= 0
意思是从dp[i - coins[0]] , dp[i - coins[1]] 是走到前一步的dp加上当前的coin一气呵成
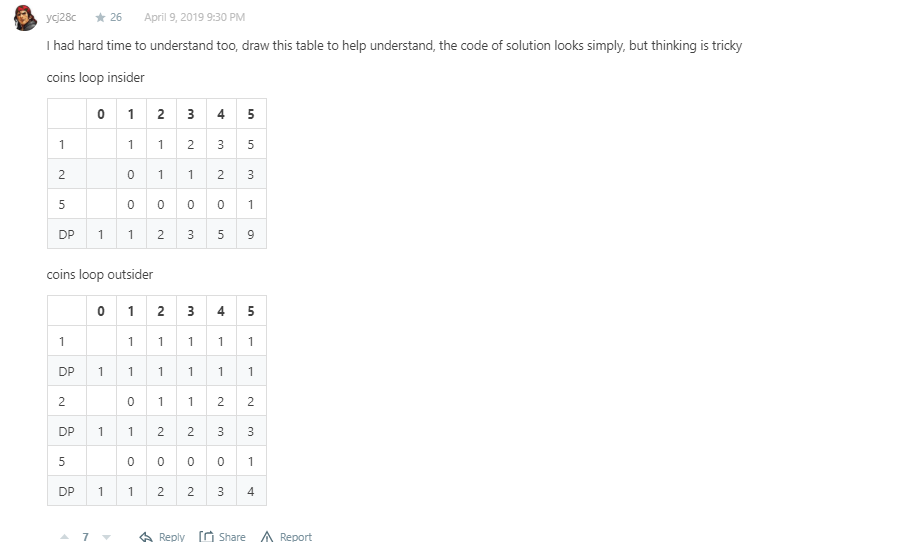
https://leetcode.com/problems/coin-change-2/discuss/176706/Beginner-Mistake%3A-Why-an-inner-loop-for-coins-doensn't-work-Java-Soln

update 10/2/2020
这题和377. Combination Sum IV有什么区别?为什么这题是coin在外循环,377是value在外循环?
猜想:这题coin change,要求所有不同的排列,那比如5 = 1+2+2,这算一个,而2+2+1,1+2+1就不算了。
但是在377中是算不同的,他叫combination sum,其实是permutaion sum。
所以在coin change中,用了一次的coin不能返回去再用,这要求我们把coin放在外循环。
而combination sum IV,我们要所有的结果,所以把nums放内循环,确保了每个value可以得到所有的combination。
继续:为什么coin change1中顺序无所谓?因为1要的是minumum number,比如2+2+1,1+2+1都是3个,所以不影响结果,但速度有影响,coin放在外面更快。




 浙公网安备 33010602011771号
浙公网安备 33010602011771号