第04次作业-树

1.学习总结

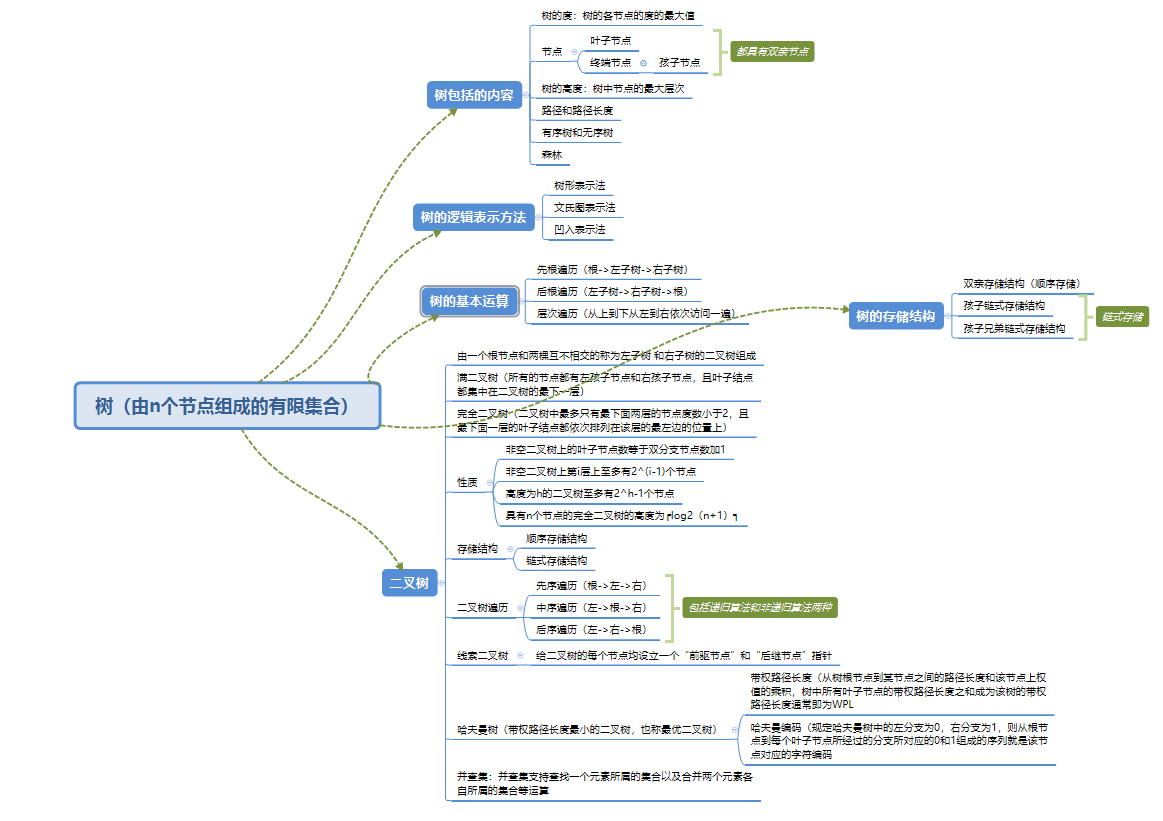
1.1树的思维导图

1.2 树结构学习体会

认识：树是一种非线性数据结构，很像自然界中的树呢样，从树根到大分支，小分支，直达叶子把数据联系起来，这种数据结构叫做树结构。树是n个节点的有限集合。值得一提的是树中只有呢些下面不在右分支的节点才能成为叶子结点。

困难：学习树所遇到的最大困难就是很难将已经懂得的内容用代码的方式转换出来，到目前为止甚至连树的建立都很困难以及表达示的转换问题。

树的结构可以解决的问题：树的前，中，后序遍历、三种计算表达式的转换、哈夫曼编码

2.PTA实验作业

2.1 题目1：二叉树操作集

2.1.1 设计思路（伪代码或流程图）

void 创建树(BTree &BT,string str)
{
    定义树T
    定义队列Q用来存放树的节点
    定义i=0用来计数
    判断str[i]!=0
	{
        BT申请空间
        将str[i]赋予BT->data
        初始化BT的左右孩子
        BT的节点入队
    }
    否则 重新进入函数

    i++;
    队列Q不为空while循环
	{
	    将队头元素赋给树T
	    元素出队
	    判断str[i]=='#'||str[i]=='0'
	    {
    		令左孩子为空
    	}
    	否则
		{
    		给T的左子树申请空间
    		将str[i]赋给左孩子
    		初始化左子树的左右孩子
    		T的左孩子入队 
	    }
    	i++;
    	判断str[i]=='#'||str[i]=='0'
		{
	    	初始化T的左孩子
	    }
    	否则
		{
	    	给T的右子树申请空间
    		将str[i]赋给右孩子
    		初始化右子树的左右孩子
    		T的右孩子入队 
    	}
    	i++; 
    }
}

2.1.2 代码截图

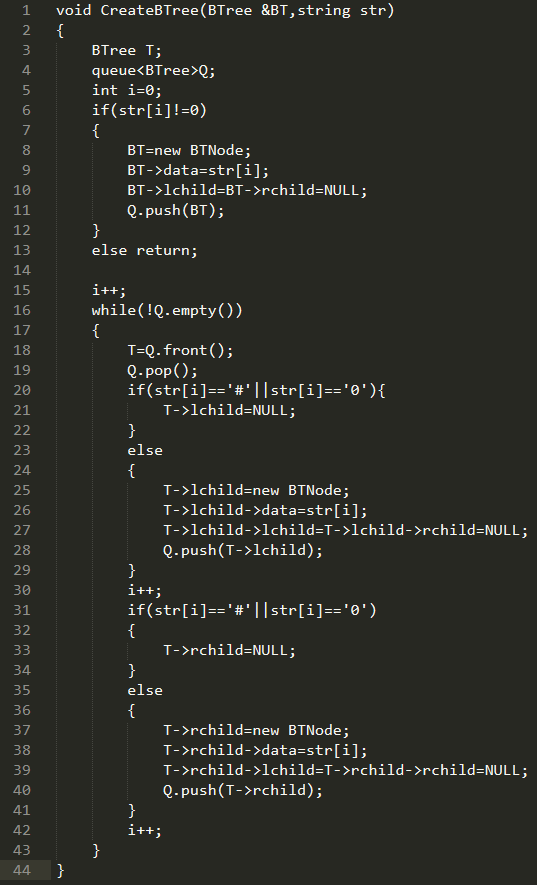
2.1.3 PTA提交列表说明。

说明：1.部分正确：一开始忽略了要将左右孩子初始化的步骤----添加 “T->lchild=T->rchild=NULL;”将左右孩子初始化。

2.2 题目2：还原二叉树

2.2.1 设计思路（伪代码或流程图）

Tree RestoreTree(int x1,int x2,int z1,int z2)
{
    创建一个根节点head并调入creatNode
    将x[x1]赋给head
    for int i = z1 to z2
    {
        判断z[i] == x[x1]
        {
            判断如果i!=z1，左子树递归带入
            判断如果i!=z1，左子树递归带入
            break;
        }
    }
    返回 head;
}
int max(int a,int b)
{
    if(a>b)return a;
    return b;
}
int Theight(Tree tree)
{
    判断tree == NULL 返回 0;
    否则 左右子树中深度最大的一个再+1;
}

2.2.2 代码截图

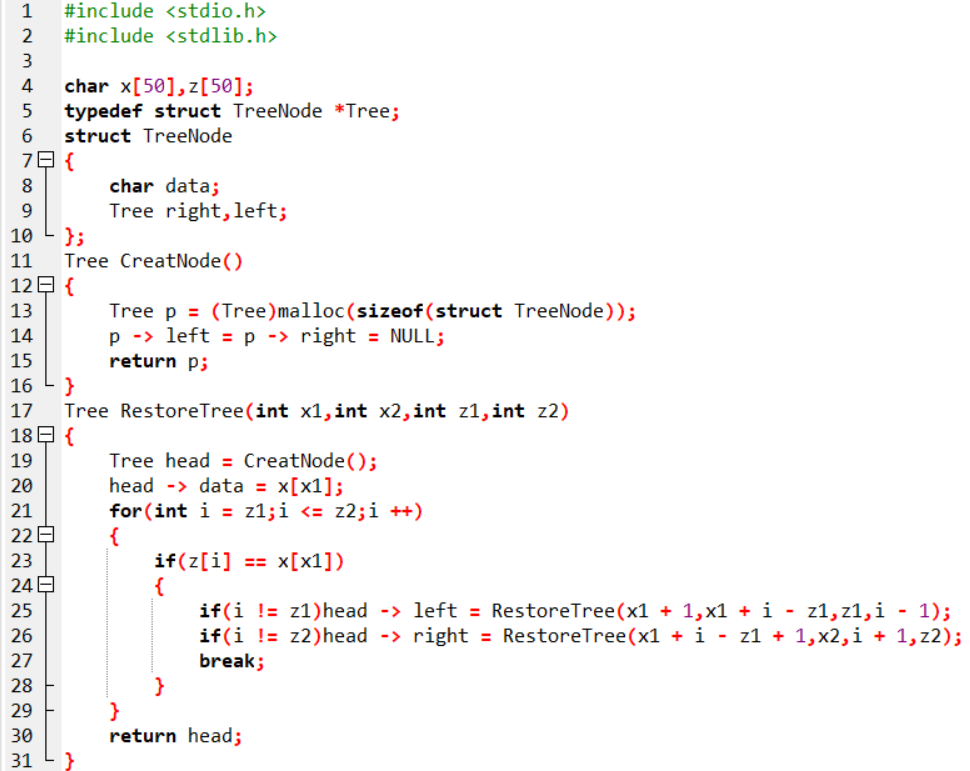
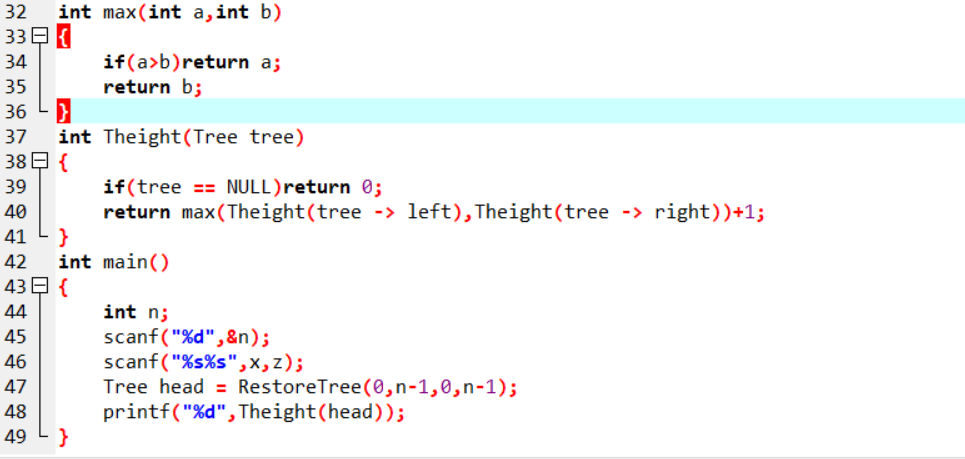
2.2.3 PTA提交列表说明。

说明：1.部分正确：一开始忽略了要将左右孩子初始化的步骤----添加 “T->lchild=T->rchild=NULL;”将左右孩子初始化。在检查完后又发现在Theight这个函数中缺少一个判断条件当树为空时。

2.3 题目3：表达式树

2.3.1 设计思路（伪代码或流程图）

void InitExpTree(BTree &T,string str)  
{
	定义栈s用于存放树的节点数据
	定义字符栈用来存放符号
	#入栈用作空栈标识
	定义i做下标
	while str[i]存在
	{
		判断str[i]不是字符
		{
			创建树T并申请空间
			将str中的数据赋给树T
			左右子树初始化
			T中数据入栈
		}
		否则
		{
			switch判断字符
			{
				"<"时
				    数据入栈op
					i++;
					break;
				"="时
					op栈顶元素出栈;
					i++;
					break;
				">"时
					创建新节点T
					将op栈顶元素赋给T
					将s的栈顶元素赋给T的右孩子
					s栈顶元素出栈
					将s站费那个元素赋给左孩子
					s栈顶元素出栈
					将此T的元素入栈s
					op栈顶元素出栈
					break;
			}
		}
	}
	while op栈顶元素不为'#'
	{
		创建新节点T
		将op栈顶元素赋给T
		将s的栈顶元素赋给T的右孩子
		s栈顶元素出栈
		判断s不为空
		{
			将s站费那个元素赋给左孩子
			s栈顶元素出栈
		}
		
		将此T的元素入栈s
		op栈顶元素出栈
	}
	将s的栈顶元素赋给T
}
double EvaluateExTree(BTree T)
{
	定义a b表示运算的两个元素
	判断T的左右孩子都不存在
	{
		返回 T->data-'0';
	}
	a=EvaluateExTree(T->lchild);
	b=EvaluateExTree(T->rchild);
	switch T此时的元素
	{
		'+'时
			返回a+b;
			break;
		'-'时 
			返回a-b;
			break;
		'*'时
			返回a*b;
			break;
		'/'时
		  判断b<1且b-1
			 {
			   打印"divide 0 error!"
		     }
			否则返回a/b;
			break;
	}
}

2.3.2 代码截图

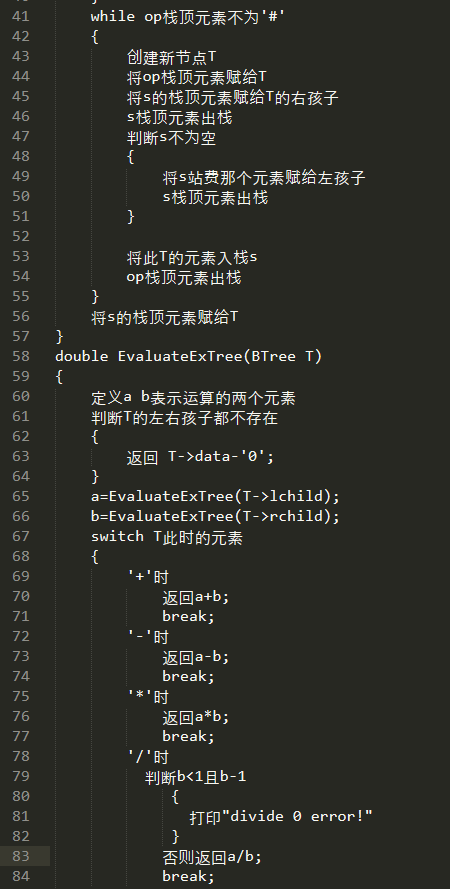
2.3.3 PTA提交列表说明。

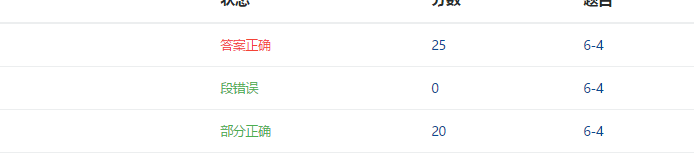
说明：1.部分正确：计算函数中除法缺少情况当除数为0时；添加这一情况当除数为0且data-1等于0时，输出错误

2.段错误：在将栈s创建进树中是缺少情况建立左子树。添加当s不为空是，将s的栈顶元素赋给T的左子树

3.截图本周题目集的PTA最后排名

暂时没有

3.1 PTA排名截图

暂时没有

3.2 我的总分：1分

4. 阅读代码

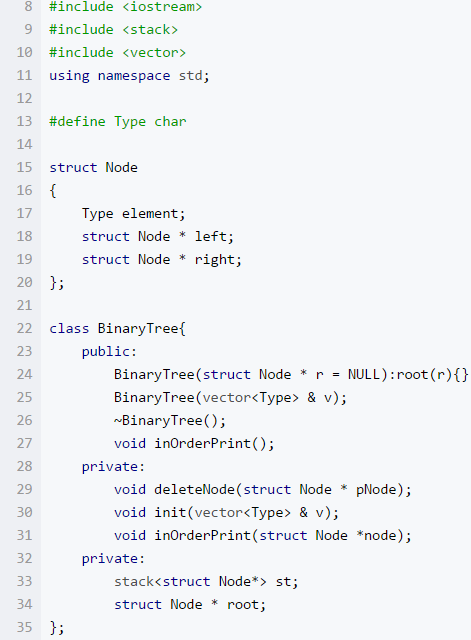
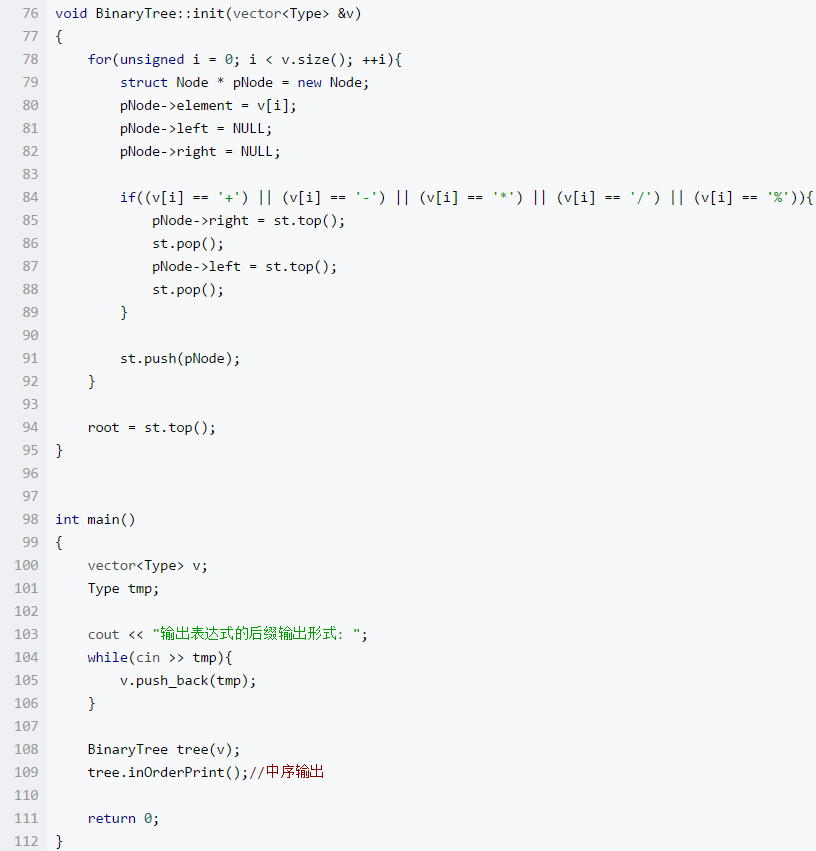
功能：这个代码功能是将表达示由后缀转换成中缀

优点：代码工整，思路明确，能够使读者很快的理解并熟悉

5. 代码Git提交记录截图