懒人需要掌握的快排-已经连续被绊倒N次了

基于最近连续被快排算法绊倒在初面。决定再此复述一遍：

• 快排的时间复杂度是O(nlogn)，空间复杂度是O(1)，是基于选择交换、分而治之的算法。在实现中用到了递归。
• 口述快排算法：
  1. 选择首位元素作为初始基准点，从基准点之后的数组最左边和最右边开始遍历数组，把大于基准点的元素交换到右边，小于基准点的元素交换到左边，知道左右指针相遇。
  2. 交换相遇点位置的元素和基准点比较，如果大于初始基准点，则直接作为新的基准点，否则交换位置。如果相遇前左右指针相减为0，则比较左指针元素和初始基准点元素。(实际为了解决这种情况，从右边开始找比基准点大的元素，这样在左边的指针不小于右边指针时的元素就可以直接和基准点替换了，为了防止找过，限制左指针小于右指针)
  3. 首次快排结束之后，基准点的左边都是比它小的元素，基准点右边都是比它大的元素。
  4. 分别对基准点左边的数组右边的数组进行快排，直到要进行快排的子数组只有一位。
  5. 递归的停止条件是i>j。
• 图解快排： https://upload-images.jianshu.io/upload_images/14579564-f4c51a3d0215acc4.png?imageMogr2/auto-orient/strip|imageView2/2/format/webp
  
• 代码抄写如下：

  public class QuickSort {
    public void sort(int[] nums,int start, int end){
        if(start>end) retun;
        int left = start,right =end,key = nums[star];
        int temp =0;
        while(left<right){
        	while(left<right && nums[right]>=key){
        		right --;
        	}
        	while(left<right && nums[left]<=key){
        		left ++;
        	}
        	temp = nums[left];
        	nums[left] = nums[right];
        	nums[right] = temp;
        }
        nums[start] = nums[left];
        nums[left] = key;
        
        sort(nums,start,left-1);
        sort(nums,left+1,end);
   }
   public static void main(String args[]) {
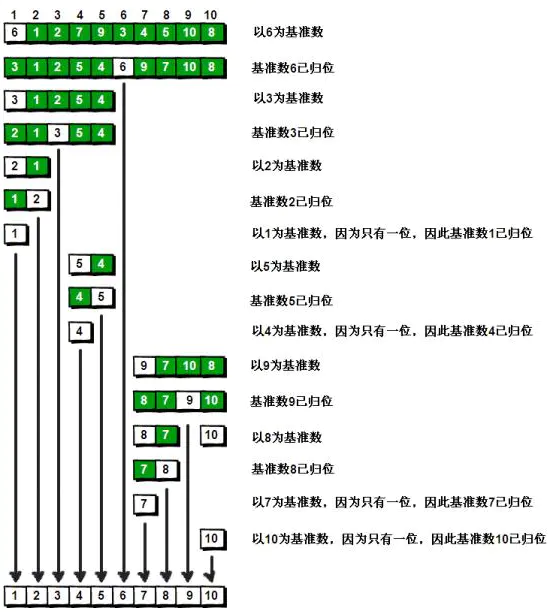
        int a[] = {6,1,2,7,9,3,4,5,10,8};
        QuickSort q = new QuickSort();
        q.sort(a,0,a.length-1);
        for(int i=0;i<a.length;i++){
            System.out.print(a[i]);
        }
    }
 }

口述针对TopK问题使用快排的思路

1. 基于快排的思想：基准点左边的元素总是小于基准点，右边的元素总是大于基准点，所以topK问题就可以转换为找到一个基准点，他的位置在len-k的地方，初始基准点是最右边的元素。
2. 如果基准点位置p大于len-k，对左边的数组进行快排，以基准点左边的元素为新的基准点，找到top(p+k-len)大的元素。
3. 如果基准点位置p小于len-k，对右边的元素找到top(len-k-p)小的元素。

• 代码如下：
  https://leetcode-cn.com/problems/smallest-k-lcci/solution/zui-xiao-kge-shu-by-leetcode-solution-o5eg/

class Solution {
    public int[] smallestK(int[] arr, int k) {
        randomizedSelected(arr, 0, arr.length - 1, k);
        int[] vec = new int[k];
        for (int i = 0; i < k; ++i) {
            vec[i] = arr[i];
        }
        return vec;
    }

    private void randomizedSelected(int[] arr, int l, int r, int k) {
        if (l >= r) {
            return;
        }
        int pos = randomizedPartition(arr, l, r);
        int num = pos - l + 1;
        if (k == num) {
            return;
        } else if (k < num) {
            randomizedSelected(arr, l, pos - 1, k);
        } else {
            randomizedSelected(arr, pos + 1, r, k - num);
        }
    }

    // 基于随机的划分
    private int randomizedPartition(int[] nums, int l, int r) {
        int i = new Random().nextInt(r - l + 1) + l;
        swap(nums, r, i);
        return partition(nums, l, r);
    }

    private int partition(int[] nums, int l, int r) {
        int pivot = nums[r];
        int i = l - 1;
        for (int j = l; j <= r - 1; ++j) {
            if (nums[j] <= pivot) {
                i = i + 1;
                swap(nums, i, j);
            }
        }
        swap(nums, i + 1, r);
        return i + 1;
    }

    private void swap(int[] nums, int i, int j) {
        int temp = nums[i];
        nums[i] = nums[j];
        nums[j] = temp;
    }
}

作者：LeetCode-Solution
链接：https://leetcode-cn.com/problems/smallest-k-lcci/solution/zui-xiao-kge-shu-by-leetcode-solution-o5eg/
来源：力扣（LeetCode）
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

参考：

1. https://www.cnblogs.com/lxy-xf/p/11338652.html
2. https://www.jianshu.com/p/55a1f740c8ef