递归分析和分治算法

递归分析一般利用的方法是主定理，辅助的方法有替换法，递归树方法~

主定理：

递归树：

主定理的证明可以通过递归树的方法进行；

 

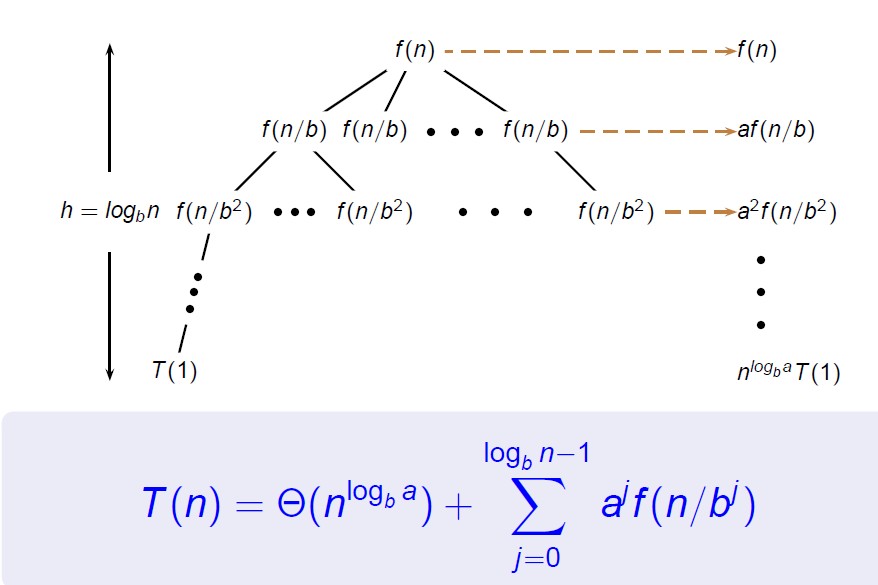
主定理适用的范围比较局限，有些情况不能被包括，这些情况就需要利用递归树的方法了，

主定理的case1是f(n)小于n^log_ba多项式时间，原定理描述为f(n)=O（n^log_ba-ε）且ε>0，它与case2中f(n)=Θ(n^log_ba)中间差一些情况，就是f(n)小于n^log_ba，但是多余的不是多项式时间；

另外就是case2和case3之间相差的部分，就是f(n)大于n^log_ba，但是如果不大于多项式时间，就不能满足主定理了；

另外一种是case3中的f(n)不满足后面的情况；

举个例子，如果最近点对中间利用快速排序进行排序，则合并时间nlgn，递归公式T（n）=2T（n/2）+nlgn，这种情况介于case2和case3，所以利用递归树：

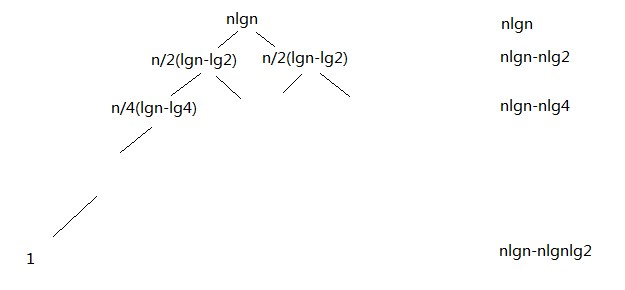
T（n）=nlgn+n(lgn-lg2)+n(lgn-lg4)+...=nlgnlgn-n(lg2+2lg2+3lg2+...+lgnlg2)=nlgnlgn-nlg2((1+lgn)lgn)/2=nlgnlgn=nlg²n;

不过这里我查到mit给的主定理和算法导论有所不同，涵盖了上面的情况，如下：

可能这算是一种情况来了；

那么这里我在取一个不满足主定理的例子~

所以主定理不满足时就利用决策树进行带入吧！如果数学计算能力比较强大还是可以计算出来的，毕竟主定理都是决策树证明的，数学能力不强表示证明有点困难...

 

不过这里有个偷懒的证明方法，直接假设f（n）是一个n^k形式的；

T（n）=aT（n/b）+n^k

T（n/b）=aT（n/b²）+（n/b）^k

...

所以T(n)=a（aT（n/b²）+（n/b）^k）+n^k=n^k（1+a/b^k+...+(a/b^k)^h)=(n^k-n^logba)/(1-a/b^k),接下来讨论a和b^k的关系决定了为n^k还是n^logba，上面如果为1则为n^klog_bn了。

简单的证明，不过不太准确；

 

替换法举一个例子如下：

    分治方法算是算法设计中一种很常见的设计方式，一般能够大大提高算法的时间复杂度的~分治的思想很简单，就是将一个问题切分为两个或者多个独立的子问题，子问题的解决方案同，子问题解决之后通过合并算法组合成更大问题的结果，所以分治算法主要有三个步骤，Divide（切分子问题的方案）、Conquer（一般子问题独立相同的，所以这里一般是递归的解决子问题）、Combine（子问题提升至更大问题的时候需要对子问题的解决方案进行合并）。分治算法还是对待不同的问题需要不同的分治方案，所以掌握缩小问题的规模的思想还是比较重要的，比较高级的动态规划和贪心也都是通过缩小问题规模提升时间复杂度的。所以感觉还是多掌握一些具体实例的分治方案，这样碰到陌生问题的时候可以像熟悉的问题靠拢，所以接下来具体分析一下算法导论中一些分治的实例。（怎么感觉map-reduce也是这么干的？）

下面的内容：1归并排序  2二分查找  3斐波那契近似求值  4大数相乘  5矩阵乘法  6最近点对

1、归并排序

Divide：一个数字序列切分为两部分，各n/2

Conquer：对切分的两个子问题分别merge-sort，子问题的性质同父问题，所以可以递归调用

Combine：对两个已经排序好的数组进行合并，两个数组开始均设置一个指针，然后向后读取，每次取最小，这样线性时间就可以对两个排序好的数组合并成为一个大的数组

实现代码：

//因为merge算法需要额外的空间，算法执行之前动态开辟，准备的算法
bool PreMergeSort(unsigned int* array,int begin,int end)
{
	unsigned int* arrayAssit = new unsigned int[end - begin + 1];
	mergeSort(array,arrayAssit,begin,end);
	delete [] arrayAssit;
	return true;
}

//merge的主程序部分，首先进行切分，找出中间位置，然后切分成前半部分merge-sort和后半部分merge-sort
bool mergeSort(unsigned int* array,unsigned int* arrayAssit,int begin,int end)
{
        //递归结束条件
	if (end == begin)
	{
		return true;
	}
	int mid = (begin+end)/2;
	mergeSort(array,arrayAssit,begin,mid);
	mergeSort(array,arrayAssit,mid+1,end);
        //合并部分
 	merge(array,arrayAssit,begin,mid,end);
	return true;
}
//递归之后的合并部分，思想就是两个指示器指示两个待合并的数组的起始位置，比较大小，每次输出小的元素，然后相应指示器++，如果一个输出完毕，则另外一个全部输出，输出的为合并好的数组
bool merge(unsigned int* array,unsigned int* arrayAssit,int begin,int mid,int end)
{
	int i,j,k;
	i = begin;
	j = mid + 1;
	k = begin;
        //比较输出小的过程
	while(i <= mid&&j<= end)
	{
		if (array[i] <= array[j])
		{
			arrayAssit[k++] = array[i++];
		}
		else
		{
			arrayAssit[k++] = array[j++];
		}
	}
        //一个输出完毕，另外一个全部输出
	while (i <= mid)
	{
		arrayAssit[k++] = array[i++];
	}
	while (j <= end)
	{
		arrayAssit[k++] = array[j++];
	}
        //临时数组拷贝至原数组
	memcpy(array+begin,arrayAssit+begin,(end-begin+1)*sizeof(array[0]));
	return true;
}

时间复杂度分析：

Divide：  Θ（1）

Conquer：2T（n/2）

Combine：Θ（n）

递归式

T（n）=　　2T（n/2）+Θ（n）+Θ（1）  n>1

         =      1                                     n=1

根据主定理，T（n）=Θ（nlgn）

2、二分查找

输入有序数组~

Divide：查找中间位置元素，比对大小

Conquer：根据上面直接把问题划分为左边查找还是右边查找~

Combine：这个问题没有合并的步骤

 

时间复杂度分析：

Divide：  Θ（1）

Conquer：T（n/2）

Combine：Θ（1）

递归式

T（n）=　　T（n/2）+Θ（1）+Θ（1） 

根据主定理，T（n）=Θ（lgn）

3、斐波那契数列

斐波那契数列的分治算法基于以下一个近似算法和以下一个矩阵计算方法：

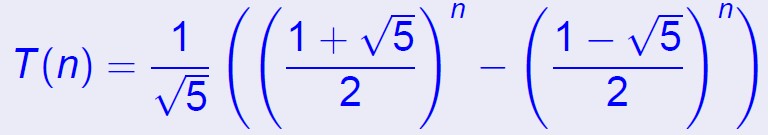
分治的思想是就是一个求pow的分治，比如pow（a，n）可以分治为pow（a，n/2）*pow（a，n/2）

Divide：Θ（1）

Conquer：T（n/2）

Combine：Θ（1）乘法

由主定理：T（n）=Θ（lgn）

代码实现：

 

//左边递归
double leftn(int n)
{
	if (n == 1)
	{
		return (1+sqrt((double)5))/2;
	}
	if (n>=2&&n%2!=0)
	{
		double tmp = leftn((n-1)/2);
		return tmp*tmp*(1+sqrt((double)5))/2;
	}
	if (n>=2&&n%2==0)
	{
		double tmp = leftn(n/2);
		return tmp*tmp;
	}
}
//右边递归
double rightn(int n)
{
	if (n == 1)
	{
		return (1-sqrt((double)5))/2;
	}
	if (n%2!=0)
	{
		double tmp = rightn((n-1)/2);
		return tmp*tmp*(1-sqrt((double)5))/2;
	}
	if (n%2==0)
	{
		double tmp = rightn(n/2);
		return tmp*tmp;
	}
}
//近似求值
double FibonaccinClose(int n)
{
	return ((leftn(n)-rightn(n))/sqrt((double)5));
}

　　

 

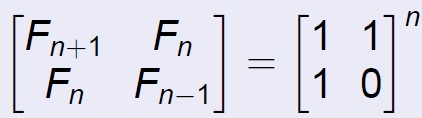
递归的相似同上，矩阵的pow分治

代码实现：

Rect FibonacciRect(int n)
{
	if (n == 0)
	{
		//  1 1
		//  1 0
		rect.x01 = 0;
		rect.x02 = 0;
		rect.x11 = 0;
		rect.x12 = 0;
		return rect;
	}
	if (n == 1)
	{
		//  1 1
		//  1 0
		rect.x01 = 1;
		rect.x02 = 1;
		rect.x11 = 1;
		rect.x12 = 0;
		return rect;
	}
	//偶数
	if (n >= 2 && n%2 == 0)
	{
		tmpRect1 = FibonacciRect(n/2);
		rect.x01 = tmpRect1.x01*tmpRect1.x01+tmpRect1.x02*tmpRect1.x11;
		rect.x02 = tmpRect1.x01*tmpRect1.x02+tmpRect1.x02*tmpRect1.x12;
		rect.x11 = tmpRect1.x11*tmpRect1.x01+tmpRect1.x12*tmpRect1.x11;
		rect.x12 = tmpRect1.x11*tmpRect1.x02+tmpRect1.x12*tmpRect1.x12;
		
		return rect;
	}
	//奇数
	if (n > 2 && n%2 == 1)
	{
		tmpRect1 = FibonacciRect((n-1)/2);
		tmpRect2.x01 = tmpRect1.x01*tmpRect1.x01+tmpRect1.x02*tmpRect1.x11;
		tmpRect2.x02 = tmpRect1.x01*tmpRect1.x02+tmpRect1.x02*tmpRect1.x12;
		tmpRect2.x11 = tmpRect1.x11*tmpRect1.x01+tmpRect1.x12*tmpRect1.x11;
		tmpRect2.x12 = tmpRect1.x11*tmpRect1.x02+tmpRect1.x12*tmpRect1.x12;

		rect.x01 = tmpRect2.x01 + tmpRect2.x02;
		rect.x02 = tmpRect2.x01;
		rect.x11 = tmpRect2.x11 + tmpRect2.x12;
		rect.x12 = tmpRect2.x11;

		return rect;
	}
}

时间复杂度：

Divide：Θ（1）

Conquer：T（n/2）

Combine：Θ（1）乘法

由主定理：T（n）=Θ（lgn）

 4、分治法求大整数相乘

c=a*b=(a1*10^n/2+a0)*(b1*10^n/2+b0)=(a1*b1)10ⁿ+(a1*b0+b1*a0)10^n/2+b0*a0

 = c0*10ⁿ+c1*10^n/2+c2

如果c1利用上面的(a1*b0+b1*a0)进行计算，

算法分析如下：

Divide：Θ（1）

Conquer：4T（n/2）

Combine：Θ（1）乘法

由主定理：T（n）=Θ（n²）

这里时间复杂度没有减少，具体原因是由于乘法的次数没有减少，所以c1修改为如下计算：（a1+a0）*（b1+b0）-（c0+c2）

这样分析就如下

Divide：Θ（1）

Conquer：3T（n/2）

Combine：Θ（1）乘法

由主定理：T（n）=Θ（n^1.585）

5、矩阵乘法

矩阵的乘法的分治和上面的很相似，也是乘法数量的减少，普通的矩阵分治：

T（n）=8T(n/2)+Θ(n²)

主定理T（n）=Θ（n³），没有时间复杂度的提高

这样减少乘法的数量：

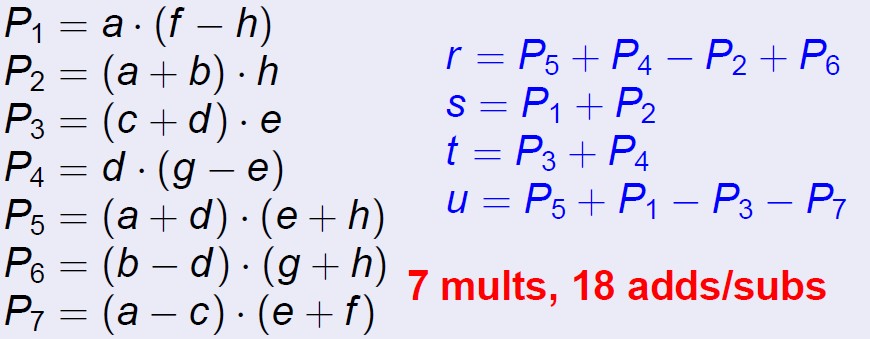
T（n）=7T(n/2)+Θ(n²)

主定理T（n）=Θ（n^2.81），

6、最近点对

最近点对的分治思想比较容易得到，就是从中部分开，然后分别求两边最短的点对，但是这里的难点在于合并，合并的时候可能出现跨越两个区域的最近点对，合并的时间复杂度如果选择不当，则会导致整个算法的时间复杂度的提高；

递归结束条件为3，3个点的时候暴力求解即可；

T（n）=2T（n/2）+？，问号及为合并的时间，如果算法想要达到nlgn的时间复杂度，则这里的？必须为线性时间的！注意，这个是重点~

合并的时候首先考虑到只需要考虑以下带状区域：这里的d为两边求取的最小的距离，中间合并只可能出现比这个距离更小的，所以要在带状区域寻找

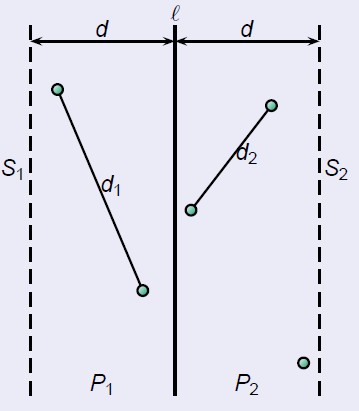
但是如果每个点暴力解决带状区域考虑最坏情况可能是n²的时间复杂度，所以不行；

所以考虑以下其中一个点，看看其需要遍历哪些点，看看是否能够减少一个点遍历的点的数量，上面是遍历所有带状区域的点，这里我们发现可以根据某个点划分一个区域：

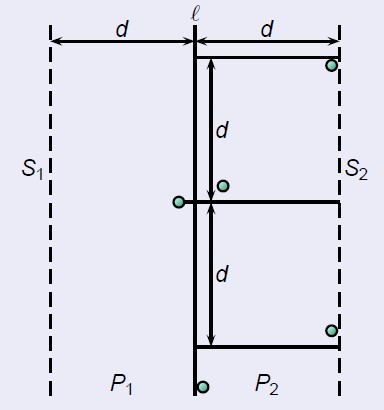
针对左边的某个点，右边划分出的矩形中最多存在6个点与其对应，所以每次只需要遍历6个点即可，这6个点是y坐标距离左边某个点最近的6个点；

 

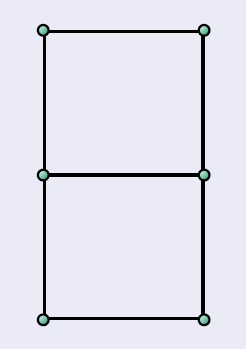
对于左边范围内的p点，最多只有6个点。这个可以反推证明，如果右边这2个正方形内有7个点与p点距离小于δ，例如q点，则q点与下面正方形的四个顶点距离小于δ，则和δ为S_L和S_R中的最小点对距离相矛盾。因此对于左边的p点，不需求出p点和右边虚线框内所有点距离，只需计算S_R中与p点y坐标距离最近的6个点，就可以求出最近点对，节省了比较次数。线性合并时间的关键保持一个按照y排序的数组，利用预处理和归并的思想~

代码如下：

 

//原理就是归并排序的合并，
void merge(point y[], point m[], int begin, int end, int mid)
{
	int i, j, k;
	for (i = begin, j = mid + 1, k = begin; i <= mid && j <= end;)
	{
		//左边开始的为i，右边开始的为j，i从begin开始，j从mid+1开始
		//然后开始比较i和j的关系，如果j小，则把j移动到i这边同时j++
		//m保存着已经排序好的
		if (m[i].y > m[j].y)
		{
			y[k++] = m[j];
			j++;
		}
		else
		{
			y[k++] = m[i];
			i++;
		}
	}
	while (i <= mid)
		y[k++] = m[i++];
	while (j <= end)
		y[k++] = m[j++];
	//将排序好的m拷贝到y中
	memcpy(m + begin, y + begin, (end - begin + 1) *sizeof(y[0]));
}

double closepair(point x[],point y[],point m[],int begin,int end,point& px,point& py)
{
	//一个点直接返回0
	if (end-begin==0)
	{
		return 0;
	}
	//小于等于3个点就不递归了，直接穷举计算
	if (end-begin<=2)
	{
		return enumpair(x,begin,end,px,py);
	}
	//取分治的点
	int mid = (begin + end)/2;
	int i,j,k;
	double dl,dr,dm;
	//这里开始把按照y坐标排序的y数组分成左边按照y排序和右边按照y排序
	//点的标识这里用到了
	for (i=begin,j=begin,k=mid+1;i<=end;i++)
	{
		if (y[i].index<=mid)
		{
			m[j++]=y[i];
		}
		else
		{
			m[k++]=y[i];
		}
	}
	//递归
	dl = closepair(x,m,y,begin,mid,px,py);
	dr = closepair(x,m,y,mid+1,end,px,py);

	dm = min(dl,dr);

	//将上面分的y合并
	merge(y,m,begin,end,mid);

	//找出带状Y'按照y排序的那部分
	for (i=begin,k=begin;i<=end;i++)
	{
		if (fabs(y[i].x-x[mid].x)<dm)
		{
			m[k++]=y[i];
		}
	}
	//然后遍历带状Y’中最短的进行
	//合并
	for (i=begin;i<k;i++)
	{
		for (j=i+1;j<k&&m[j].y - m[i].y < dm;j++)
		{
			double tmp = compudis(m[i],m[j]);
			if (tmp<(dm<shortest?dm:shortest))
			{
				//记录最小距离以及最近点对
				shortest=tmp;
				px.x = m[i].x;
				px.y = m[i].y;
				py.x = m[j].x;
				py.y = m[j].y;
			}
		}
	}
	return shortest;
}

上面算法中寻找6个点的时候排序后又线性的查找了距离的6个点，所以没有利用上面已经证明的，但是还是保持了线性的性质。可以直接在排序数组中利用6个点的性质。

最近点对的合并算法比较复杂，一般比较难的分治问题的难点就在于合并的难处，它最终也限制了算法的时间复杂度，所以重点理解下最近点对。

T（n）=2T（n/2）+Θ（n）

所以T（n）=nlgn  ！

 

有错误请指正~转载请注明出处，谢谢.