基础查找算法（四）哈希查找

一 定义

哈希查找是一种高效的数据检索技术，它通过特定的哈希函数将关键字直接映射到存储位置，从而实现近乎常数时间复杂度的查找性能

二 算法特性

特性	说明
核心思想	通过哈希函数建立关键字到存储地址的直接映射
时间复杂度	平均接近O(1)，最坏情况O(n)
空间复杂度	O(n)，需要预分配哈希表空间
关键组件	哈希函数、冲突解决方法、装载因子管理
主要优点	查找效率极高，适合大规模数据
主要缺点	需要处理冲突，不支持顺序遍历

三 算法原理与工作机制

3.1 整体流程

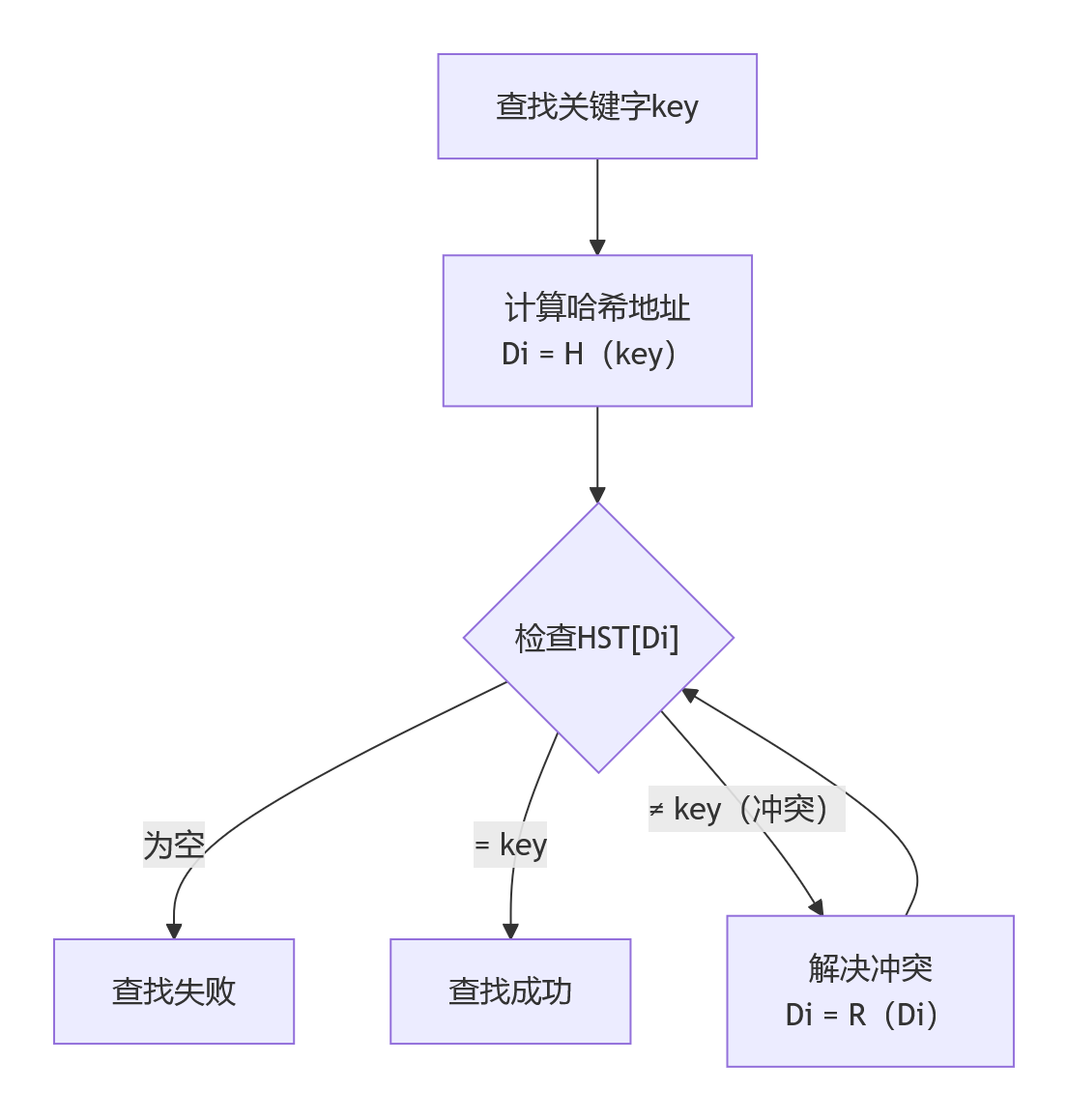
哈希查找的核心机制可以分为三个关键步骤，其整体工作流程如下图所示，体现了从关键字到最终定位的完整过程：

3.2 详细步骤

具体来说，每个步骤的细节如下：

3.2.1 哈希函数计算：

• 哈希函数 H(key)将关键字 key映射为哈希表中的位置索引 Di。例如，使用简单的除留余数法：H(key) = key % p，其中 p为不大于哈希表长的质数，这有助于哈希值分布均匀。
• 设计良好的哈希函数应具备计算速度快、输出值分布均匀的特点，以尽量减少冲突。

3.2.2 地址检查与冲突处理：

• 计算得到 Di后，检查哈希表中该位置的状态。
• 查找成功：若 HST[Di]等于 key，则查找成功。
• 发生冲突：若 HST[Di]已被其他不等于 key的元素占用，则发生哈希冲突，此时需使用预设的冲突解决方法。
• 查找失败：若 HST[Di]为空，则表示查找失败。

3.2.3 冲突解决方法：

• 开放定址法：按照既定规则（如线性探测 Di = (Di + 1) % m）寻找哈希表中的下一个空闲位置。
• 链地址法：将所有哈希到同一地址的元素存储在一个链表中，查找时遍历该链表直至找到目标关键字或到达链表末尾。

四 性能分析

哈希查找的性能主要受以下因素影响：

• 装载因子（Load Factor）：α = 表中已填入元素个数 / 哈希表长度。α越大，表明哈希表越满，发生冲突的可能性越高。通常需要通过扩容（Rehashing）来控制 α，以维持较高的查找效率。
• 哈希函数：均匀性好的哈希函数能有效减少冲突。
• 冲突处理方法：
  • 链地址法：查找成功时平均查找长度（ASL）约为 1 + α/2；查找失败时平均查找长度（ASL）约为 α + e^(-α)。
  • 线性探测法：查找成功时平均查找长度（ASL）约为 (1 + 1/(1-α)) / 2；查找失败时平均查找长度（ASL）约为 (1 + 1/(1-α)^2) / 2。随着 α增大（尤其接近1时），性能下降非常明显。

五 代码实现

5.1 c 语言

以下是使用C语言实现的哈希表，采用除留余数法作为哈希函数，线性探测法处理冲突。

5.1.1 代码

#include <stdio.h>
#include <stdlib.h>
#define SIZE 7 // 哈希表大小
#define EMPTY -1 // 空位置标记

// 哈希表结构
typedef struct {
    int *data; // 存储数据的数组
    int count; // 当前元素个数
} HashTable;

// 初始化哈希表
void initHashTable(HashTable *ht) {
    ht->data = (int *)malloc(SIZE * sizeof(int));
    for (int i = 0; i < SIZE; i++) {
        ht->data[i] = EMPTY; // 初始化为空
    }
    ht->count = 0;
}

// 哈希函数：除留余数法
int hashFunction(int key) {
    return key % SIZE;
}

// 插入元素
void insert(HashTable *ht, int key) {
    if (ht->count == SIZE) {
        printf("Hash table is full!\n");
        return;
    }
    int index = hashFunction(key);
    // 线性探测解决冲突
    while (ht->data[index] != EMPTY) {
        index = (index + 1) % SIZE; // 找下一个位置
    }
    ht->data[index] = key;
    ht->count++;
}

// 查找元素
int search(HashTable *ht, int key, int *comparisons) {
    *comparisons = 0;
    int index = hashFunction(key);
    int startIndex = index;
    do {
        (*comparisons)++;
        if (ht->data[index] == key) {
            return index; // 查找成功
        }
        if (ht->data[index] == EMPTY) {
            return -1; // 遇到空位，查找失败
        }
        index = (index + 1) % SIZE; // 继续探测
    } while (index != startIndex); // 回到起点则说明已遍历全表
    return -1; // 查找失败
}

// 打印哈希表
void printHashTable(HashTable *ht) {
    printf("Hash Table: ");
    for (int i = 0; i < SIZE; i++) {
        if (ht->data[i] != EMPTY) {
            printf("[%d]:%d ", i, ht->data[i]);
        } else {
            printf("[%d]:NULL ", i);
        }
    }
    printf("\n");
}

int main() {
    HashTable ht;
    initHashTable(&ht);
    
    int keys[] = {19, 14, 23, 1, 68};
    int n = sizeof(keys) / sizeof(keys[0]);
    
    // 插入数据
    for (int i = 0; i < n; i++) {
        insert(&ht, keys[i]);
    }
    printHashTable(&ht);
    
    // 测试查找
    int testKeys[] = {14, 68, 100};
    for (int i = 0; i < 3; i++) {
        int comps;
        int result = search(&ht, testKeys[i], &comps);
        if (result != -1) {
            printf("Key %d found at index %d, comparisons: %d\n", testKeys[i], result, comps);
        } else {
            printf("Key %d not found, comparisons: %d\n", testKeys[i], comps);
        }
    }
    free(ht.data);
    return 0;
}

5.1.2 代码解释

• 哈希表初始化：initHashTable函数将哈希表所有位置初始化为 EMPTY（-1），表示空位。
• 哈希函数：hashFunction使用简单的除留余数法（key % SIZE）计算初始位置。
• 插入操作：insert函数先计算哈希地址，若发生冲突，则使用线性探测（每次向后移动一位）寻找空位插入。
• 查找操作：search函数是核心。它从哈希地址开始线性探测，成功条件是找到关键字；失败条件是遇到空位或回到起点。comparisons参数记录比较次数，用于计算ASL。
• 冲突解决：线性探测法 index = (index + 1) % SIZE顺序查找下一个位置。

六 相似算法比较

算法	数据结构	平均时间复杂度	优点	缺点	适用场景
哈希查找	哈希表	O(1)	查找极快，插入删除效率也高	需处理冲突，空间开销大，不支持顺序相关操作	频繁的等值查询，缓存系统，字典
顺序查找	数组/链表	O(n)	实现简单，无需排序	效率低，数据量大时慢	小规模数据或无序数据
二分查找	有序数组	O(log n)	效率高	要求数组有序，插入删除成本高	静态有序数据的查找
二叉排序树查找	BST	O(log n)	支持动态集，保持顺序	可能退化为O(n)，需平衡操作	动态数据集合，需要顺序性

七 平均查找长度（ASL）计算详解

平均查找长度（ASL）是评估哈希表性能的关键指标。

7.1 查找成功的ASL（ASL_succ）

公式：ASL_succ = (所有关键字的比较次数之和) / 关键字个数
示例计算：
对关键字序列 {19, 14, 23, 1, 68}，哈希函数 H(key) = key % 7，用线性探测解决冲突。构建的哈希表如下：

哈希表查找过程示例

地址	关键字	比较次数	说明
0	14	1	直接命中
1	1	2	发生冲突，第2次比较命中
2	23	1	直接命中
3	68	2	发生冲突，第2次比较命中
4			空槽
5	19	1	直接命中
6			空槽

各关键字查找成功的比较次数计算如下：

• 14：H(14)=0，一次比较成功。次数=1
• 19：H(19)=5，一次比较成功。次数=1
• 23：H(23)=2，一次比较成功。次数=1
• 1：H(1)=1，但与地址1的关键字（14）冲突；线性探测到地址2（被23占用），继续探测地址3（空），插入。查找时，H(1)=1，比较地址1（14，≠1），继续比较地址2（23，≠1），再比较地址3（1，匹配）。次数=3
• 68：H(68)=5，与19冲突；探测地址6（空），插入。查找时，H(68)=5，比较地址5（19，≠68），继续比较地址6（68，匹配）。次数=2

ASL_succ = (1 + 1 + 1 + 3 + 2) / 5 = 8/5 = 1.6

7.2 查找不成功的ASL（ASL_unsucc）

公式：ASL_unsucc = (从每个可能的哈希地址出发查找失败所需的比较次数之和) / 哈希表长度（或可能的哈希地址总数）
示例计算：
针对上述哈希表，计算每个哈希地址的查找失败比较次数（直到遇到空位）：

哈希表查找失败比较过程分析

哈希地址	查找失败比较过程（直到遇到空位）	比较次数
0	地址0(14,非空且≠目标) → 地址1(1,非空且≠目标) → 地址2(23,非空且≠目标) → 地址3(68,非空且≠目标) → 地址4(空，停止)	5
1	地址1(1,非空且≠目标) → 地址2(23,非空且≠目标) → 地址3(68,非空且≠目标) → 地址4(空，停止)	4
2	地址2(23,非空且≠目标) → 地址3(68,非空且≠目标) → 地址4(空，停止)	3
3	地址3(68,非空且≠目标) → 地址4(空，停止)	2
4	地址4(空，停止)	1
5	地址5(19,非空且≠目标) → 地址6(空，停止)	2
6	地址6(空，停止)	1
ASLunsucc = (5 + 4 + 3 + 2 + 1 + 2 + 1) / 7 = 18/7 ≈ 2.57

八 总结

哈希查找是一种极其高效的查找技术，其核心在于通过哈希函数建立关键字到存储地址的直接映射。

• 核心优势：在理想情况下能达到常数级别的平均查找时间，使其非常适合频繁的等值查询和大规模数据处理。
• 关键挑战：性能高度依赖于哈希函数的设计（追求均匀分布）和装填因子α的控制。α过高会导致冲突激增，性能劣化。
• 选择权衡：哈希查找以空间换取时间，且通常不支持范围查询或顺序遍历。若应用需要这些特性，应考虑二叉排序树（如AVL树、红黑树）或B树等结构。
• 实践要点：在实际应用中，需根据数据特性选择高效的哈希函数（如DKDRHash、MurmurHash），并结合场景（内存敏感与否）选择合适的冲突解决方法（链地址法通常更稳定）。理解ASL有助于评估和调优哈希表性能。