基础排序算法（八）基数排序

一 基数排序

在众多排序算法中，基数排序（Radix Sort）以其独特的“按位分配”思想脱颖而出。它不通过直接比较元素的大小来进行排序，而是将整数按位数逐位切割，并根据每位上的数字进行分配和收集，从而最终实现整体有序。

1.1 特性总结

特性	描述
核心思想	非比较排序：将整数按位数切割，根据每个位上的数字（基数）进行多轮的分配和收集，最终使整个序列有序
时间复杂度	O(d × (n + k)) • n: 元素个数 • d: 最大数字的位数 • k: 每位可能的取值范围（如十进制中 k=10）
空间复杂度	O(n + k)，需要额外的空间来存放"桶"以及一些辅助数组
稳定性	稳定。在每一轮的分配和收集中，相等元素的相对顺序会被保持
主要优势	• 当 d 较小且 n 较大时，效率可以非常高 • 是稳定的排序算法
主要劣势	• 需要额外的内存空间 • 通常仅适用于整数、字符串等有固定"位"概念的数据类型

1.2 算法工作原理

基数排序的运作过程可以清晰地分为“分配”和“收集”两大阶段，并且通常按照从最低有效位（LSD - Least Significant Digit）开始处理。下图以数组 [170, 45, 75, 90, 802, 24, 2, 66]为例，展示了其基于LSD方法的排序过程：

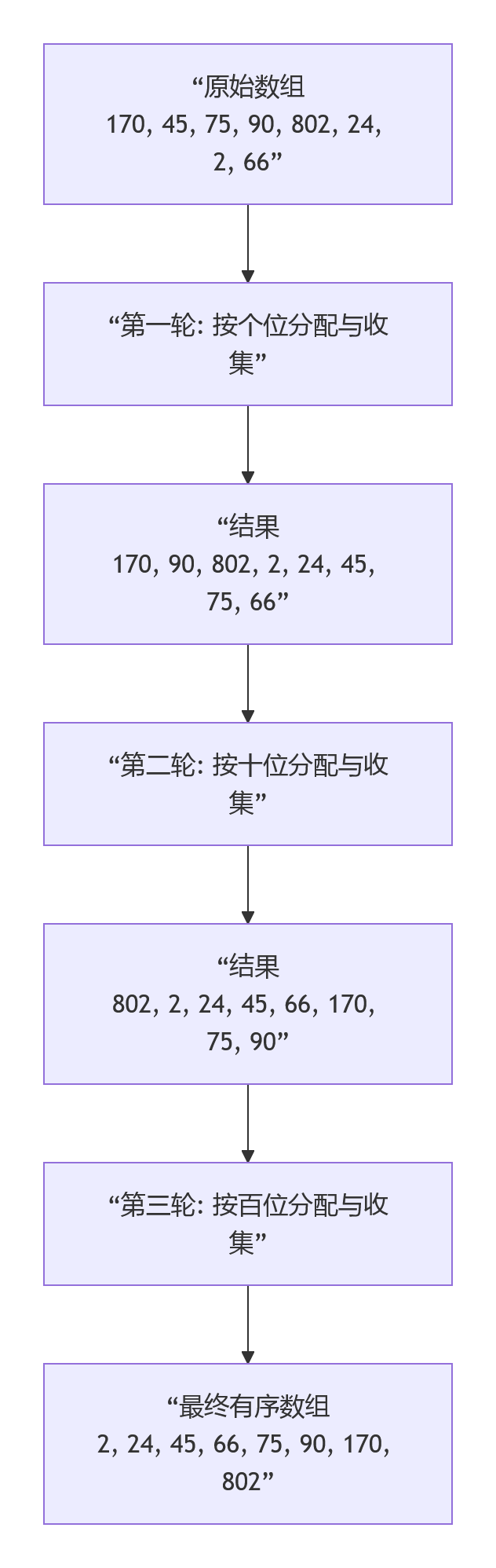
1. 确定最大位数：首先，遍历整个数组，找到数值最大的数字。这个最大值的位数 d决定了我们需要进行多少轮“分配-收集”操作。例如，最大数802有3位，所以需要3轮。
2. 分配：从最低位（个位）开始，到最高位（百位、千位等），依次进行以下操作：

• 创建10个“桶”（对应数字0-9）。
• 遍历数组，根据当前位上的数字，将每个元素放入对应的桶中。

3. 收集：按照桶的编号顺序（0号桶，1号桶，...，9号桶），依次将每个桶中的元素取出，并按放入的顺序放回原数组。这一轮操作完成后，数组相对于当前位及其之前处理过的低位来说，就是有序的。
4. 重复：对下一位（十位、百位...）重复步骤2和3，直到处理完最高位。此时，整个数组便完全有序了。

• 为什么从最低位开始？
  LSD方法之所以有效，是因为每一轮的排序都是稳定的。虽然先排序低位可能会打乱高位已有的顺序，但由于排序是稳定的，高位相同的数字在低位排序后的相对顺序会被保留。这样，当处理到高位时，高位数字大的自然会排在后面，而高位数字相同时，其顺序则由之前稳定的低位排序结果决定，从而最终实现整体有序
  。

1.3 复杂度分析

1.3.1 时间复杂度 O(d * (n + k)) 的由来：

算法需要进行 d轮操作。
在每一轮中，“分配”过程需要遍历整个数组（n个元素），时间复杂度为 O(n)。“收集”过程需要遍历 k个桶（通常 k=10），时间复杂度为 O(k)。
因此，总时间复杂度为 O(d * (n + k))。
当 d较小（即最大数字的位数不多）且 k不算太大时，基数排序的效率可以接近线性时间复杂度 O(n)，这在某些场景下优于基于比较的排序算法（如快速排序、归并排序的 O(n log n)） 。

1.3.2 空间复杂度 O(n + k) 的由来：

算法需要额外的空间来存放 k个桶。每个桶在最坏情况下可能需要存储 n个元素（虽然这种情况极少），但更常见的实现会使用链表或动态数组来优化空间使用。此外，通常还需要一个辅助数组（大小 O(n)）来暂存收集结果。
因此，总空间复杂度为 O(n + k)。

1.4 使用场景与限制

1.4.1 理想场景：

• 待排序元素是整数或具有固定长度“位”概念的数据（如字符串、定长数字编码如电话号码、IP地址等）。
• 数据规模 n较大，但最大值的位数 d相对较小。
• 需要稳定的排序结果。
• 内存空间相对充足。

1.4.2 不适用场景：

• 待排序数据是浮点数（因其内部表示复杂，难以直接按位处理）。
• 数据范围极大（即 d很大），这会显著增加排序轮数，降低效率。
• 内存限制严格的环境。

1.5 代码实现

1.5.1 c 语言实现

以下是基数排序的一个C语言实现示例，采用了LSD方式，并使用了计数排序的思想来优化每一轮的分配和收集过程

#include <stdio.h>
#include <stdlib.h>
#include <string.h> // 用于 memcpy

// 找出数组中的最大值
int getMax(int arr[], int n) {
    int max = arr[0];
    for (int i = 1; i < n; i++) {
        if (arr[i] > max) {
            max = arr[i];
        }
    }
    return max;
}

// 基于指定位数（exp）进行计数排序
void countSortByDigit(int arr[], int n, int exp) {
    int* output = (int*)malloc(n * sizeof(int)); // 输出数组
    int count[10] = {0}; // 计数数组，初始化为0

    // 统计每个数字（当前位）出现的次数
    for (int i = 0; i < n; i++) {
        int digit = (arr[i] / exp) % 10;
        count[digit]++;
    }

    // 计算累积计数，count[i] 现在表示小于等于i的数字的个数
    for (int i = 1; i < 10; i++) {
        count[i] += count[i - 1];
    }

    // 从后往前遍历原数组，将元素放入output中的正确位置（为了保持稳定性）
    for (int i = n - 1; i >= 0; i--) {
        int digit = (arr[i] / exp) % 10;
        output[count[digit] - 1] = arr[i];
        count[digit]--;
    }

    // 将排序好的 output 数组复制回原数组 arr
    for (int i = 0; i < n; i++) {
        arr[i] = output[i];
    }

    free(output); // 释放动态分配的数组
}

// 基数排序主函数
void radixSort(int arr[], int n) {
    int max = getMax(arr, n);

    // 从个位开始，对每一位进行计数排序
    for (int exp = 1; max / exp > 0; exp *= 10) {
        countSortByDigit(arr, n, exp);
    }
}

// 打印数组
void printArray(int arr[], int n) {
    for (int i = 0; i < n; i++) {
        printf("%d ", arr[i]);
    }
    printf("\n");
}

// 主函数测试
int main() {
    int arr[] = {170, 45, 75, 90, 802, 24, 2, 66};
    int n = sizeof(arr) / sizeof(arr[0]);

    printf("排序前的数组: \n");
    printArray(arr, n);

    radixSort(arr, n);

    printf("排序后的数组: \n");
    printArray(arr, n);

    return 0;
}

1.5.2 代码关键点解释

• getMax函数：用于确定数组中最大的数，从而知道需要排序的轮数（最大数的位数）。
• countSortByDigit函数：这是核心辅助函数，负责根据特定的位（exp，如1表示个位，10表示十位）进行一趟稳定的排序（本例使用了计数排序的思想）。它统计每个数字出现的次数，计算累积计数以确定元素在输出数组中的位置，然后从后往前遍历原数组以确保稳定性，最后将结果复制回原数组。
• radixSort主函数：控制整个排序流程。通过循环，依次对个位、十位、百位...直至最高位调用 countSortByDigit函数。
• 稳定性：在 countSortByDigit函数中，从数组末尾开始遍历并将元素放入输出数组，这个操作保证了相等数字（在当前位上）的原始相对顺序得以维持，从而使基数排序是稳定的。

1.6 与常见排序算法比较

算法	平均时间复杂度	最坏时间复杂度	空间复杂度	稳定性	核心思想与适用场景
基数排序	O(d × (n + k))	O(d × (n + k))	O(n + k)	稳定	非比较排序。适用于整数、字符串等，当d较小且n较大时效率高。
快速排序	O(n log n)	O(n²)	O(log n)	不稳定	分治与比较。平均性能优异，是通用排序的常用选择，但对数据分布敏感，最坏情况性能差。
归并排序	O(n log n)	O(n log n)	O(n)	稳定	分治与比较。性能稳定，是稳定的O(n log n)排序，常用于外部排序和对稳定性有高要求的场景，但需要O(n)额外空间。
堆排序	O(n log n)	O(n log n)	O(1)	不稳定	比较排序。原地排序，最坏情况也能保证O(n log n)，但常数因子较大，缓存不友好。
计数排序	O(n + k)	O(n + k)	O(n + k)	稳定	非比较排序。当整数范围k不大时极其高效，但k过大时空间消耗巨大。

从对比中可以看出，基数排序的主要优势在于其非比较的特性，在满足特定条件（数据有固定“位”、位数d不大）时，性能非常出色，并且它是稳定的。然而，其应用场景有局限性，且需要额外的内存空间。

1.7 总结

总的来说，基数排序是一种基于位”进行分配和收集的高效、稳定的非比较排序算法。其性能与待排序数据的最大位数密切相关，在处理整数、字符串等具有固定“位”概念且位数不多的数据时，优势明显。
理解基数排序的关键在于掌握其“分配-收集”的核心流程，以及LSD方法背后依靠稳定排序来保证最终顺序正确的原理。虽然它在通用性上不如快速排序等算法，但在特定的问题域内，基数排序提供的线性时间复杂度的潜力使其成为一个非常有价值的工具。